| 极移时间序列建模及预测 |
地球自转轴与地球表面的交点称为地极,因地球自转轴在地球表面及内部物质运动的综合作用下其位置在不断发生变化,所以这也导致了地极的位置在不断的移动,这种现象被称为极移[1-3]。极移同时也是描述地球自转的一个重要物理量,它与日长变化构成了地球定向参数(earth orientation parameters, EOP)[3]。目前获取这些参数主要是基于甚长基线干涉测量(very long baseline interferometry, VLBI)、激光测卫(satellite laser ranging, SLR)、全球卫星导航定位系统(global satellite navigation and positioning system, GNSS)以及DORIS等现代空间大地测量技术。虽然观测值精度高,但数据获取繁琐、数据处理过程复杂,导致解算结果滞后而无法获得实时的相关参数,所以对各参数进行高精度的模型拟合以及预测研究就很有必要。高精度极移的预测在地球参考框架建立和维持、激光测卫、天球动力学、人造卫星的导航和定轨等领域均具有重大意义[4]。国内外学者提出了诸多用于极移预报的模型,大致可分为线性模型[5]、非线性模型[6, 7]、联合预报[7]3类。本文选用自回归滑动平均混合模型以及一阶差分自回归滑动平均混合模型,基于R软件,利用国际地球自转服务(International Earth rotation service, IERS)提供的极移时间序列来进行建模及预测。
1 模型拟合 1.1 数据选择早在19世纪人们就已经开始使用传统的光学测量仪器对极移进行观测[4],但因受到大气环境、仪器测量精度、观测者的人为因素等的影响很大,精度较差。直到20世纪60年代,现代空间大地测量技术出现后,极移的观测精度才有了很大提高。
本文所使用的极移观测历史数据是国际地球自转服务提供的EOP 14 C04 (IAU2000A)序列,该序列提供了1962-01-01-2018-11-14(截至2018-12-15)的极移数据。为了保证本次使用的极移历史观测数据在精度上的一致性,最终选用的极移观测数据时间段为2001-01-01-2018-09-30,时间序列图如图 1所示,余下的实测数据用于模型预测精度验证。
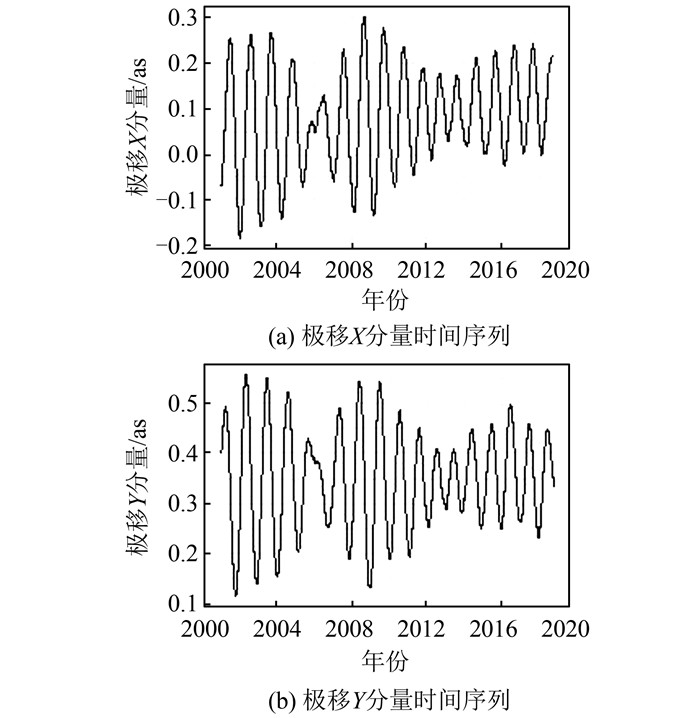 |
| 图 1 2001-01-01-2018-09-30极移时间序列 Fig.1 Polar Motion Time Series in 2001-01-01 to 2018-09-30 |
1.2 模型识别
本文选用自回归滑动平均(auto-regressive moving average, ARMA)模型,分别对极移X、Y分量进行建模。自回归滑动平均模型包括滑动平均(moving average, MA)、自回归以及自回归滑动平均混合模型[8]。其中q阶的滑动平均过程简记为MA(q)可表示为:
| $ {Y_t} = {e_t} - {\theta _1}{e_{t - 1}} - {\theta _2}{e_{t - 2}} - \cdots - {\theta _q}{e_{t - q}} $ | (1) |
p阶自回归过程满足方程:
| $ {Y_t} = {\varphi _1}{Y_{t - 1}} + {\varphi _2}{Y_{t - 2}} + \cdots + {\varphi _p}{Y_{t - p}} + {e_t} $ | (2) |
自回归滑动平均混合模型中部分是自回归,部分是滑动平均,这样就能够拟合更普遍的时间序列。阶数分别为p和q阶的自回归滑动平均混合过程,简记为ARMA(p, q),可表示为:
| $ \begin{array}{*{20}{c}} {{Y_t} = {\varphi _1}{Y_{t - 1}} + {\varphi _2}{Y_{t - 2}} + \cdots + {\varphi _p}{Y_{t - p}} + {e_t} - }\\ {{\theta _1}{e_{t - 1}} - {\theta _2}{e_{t - 2}} - \cdots - {\theta _q}{e_{t - q}}} \end{array} $ | (3) |
对于MA(q)模型,当滞后超过q时,自相关函数(auto-correlation function, ACF)为零,因此,样本自相关函数是MA过程阶数的一个良好指示器。为了识别AR(auto-regressive)模型,需使用偏自相关函数(partial auto-correlation function, PACF),对于AR(p)过程的偏自相关数在滞后超过p阶时截尾,判定依据如表 1所示。对于自回归滑动平均混合模型的阶数判定需使用扩展的自相关函数。
| 表 1 ARMA模型ACF和PACF的一般特征 Tab.1 General Characteristics of ARMA Model ACF and PACF |
 |
若时间序列Yt经过d次差分Wt=▽dYt是一个平稳ARMA过程,则Yt称为自回归滑动平均求和模型(auto-aegressive integrated moving average, ARIMA)[8]。差分过后的时间序列Wt若服从ARMA(p, q)模型,则可以将原时间序列简记为ARIMA(p, d, q)。一阶差分ARMA模型,是首先通过一阶差分处理,用以增强数据的平稳性,再利用ARMA模型来拟合获得的差分数据。若时间序列为Yt,则一阶差分可表示为:
| $ \nabla {Y_t} = {Y_t} - {Y_{t - 1}} $ | (4) |
选用了扩展的自相关函数(extended auto-correlation function, EACF)用以确定ARMA模型的阶数,其原理可理解为:首先通过迭代回归从混合ARMA模型中“滤出”自回归部分,确定自回归过程的阶数并得到一个纯滑动平均过程,此时该过程的ACF将具有截尾特征,再根据截尾的阶数确定滑动平均过程的阶数,从而确定了自回归以及滑动平均各过程对应的阶数[8]。
ARMA(p, q)过程在理论上有一个由零构成的三角模式,其左上角对应着ARMA模型的阶数,且模型选取应遵从简约原则。所以可以确定极移X分量模型为ARMA(2, 8)。
同理,计算得到极移Y分量的扩展自相关函数并根据同样的判定方法,可以确定极移Y分量的模型为ARMA(2, 9)。
1.2.2 ARIMA模型识别首先分别对极移X、Y分量做一阶差分处理,得到差分后极移分量的时间序列图,如图 2所示。同样基于扩展自相关函数可确定经过一阶差分处理后的极移序列ARMA模型的阶数,因判断方法相同这里不进行详述。可确定一阶差分极移X、Y分量的模型分别为ARMA(2, 8)和ARMA(2, 7),简记为ARIMA(2, 1, 8) 和ARIMA(2, 1, 7)。
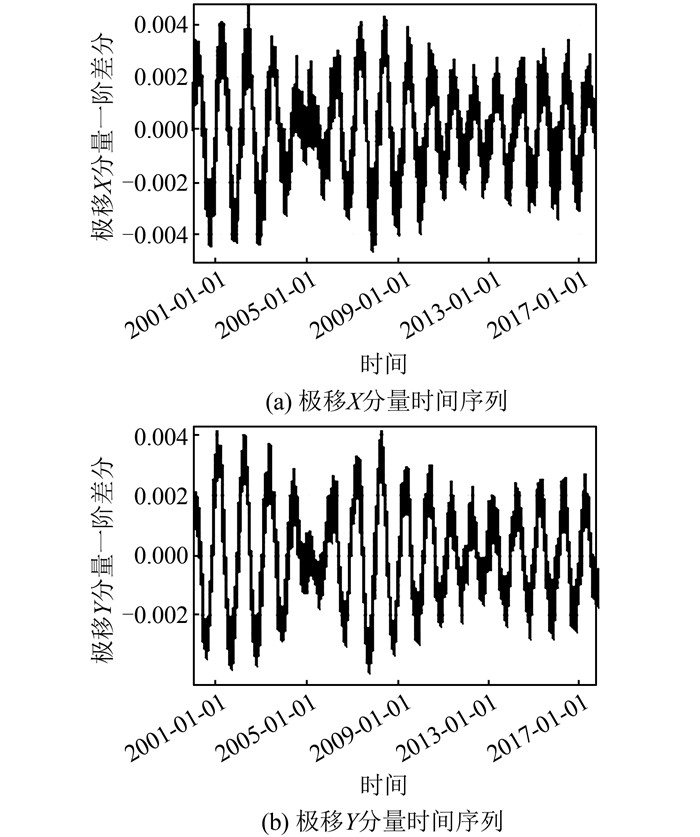 |
| 图 2 极移一阶差分时间序列图 Fig.2 Single Differential Time Series Diagram of PM |
1.3 模型诊断
模型评价是检验模型的拟合优度,如果模型被正确识别,并且参数估计充分接近真值,那么残差就应该近似具有白噪声的性质。它们的表现就像那些独立同分布的具有零均值和相同标准差的正态变量[8],与这些性质对比,有助于评价该模型的拟合优度。
1.3.1 残差的正态性检验分位数-分位数图是一种有效评估正态性的工具,因此使用其来检验残差的正态性。经检验:虽然在首尾有几个点偏离了直线,但是其整体上非常接近一条直线,即表明不能拒绝模型误差项是正态分布的假设,残差的正态性检验通过。
1.3.2 Ljung-Box检验为了检验模型拟合优度及噪声项的独立性,所以采用了Ljung-Box检验。图 3中展示了3种诊断工具从左到右分别对应:标准残差的序列图、残差的样本ACF、K从5~15的Ljung-Box检验统计量的p值,在5%处的水平线有助于判断p值的大小。如果模型是适当的,则残差的时间序列期望图形是一个围绕零水平线的,无任何趋势的长方形散点图[8]。可以看出极移X、Y分量拟合模型的标准残差与期望图形表现一致,并且最大值均未超过4 mas,即表明了选用模型的合理性。
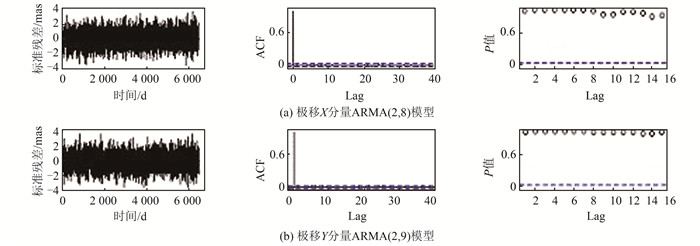 |
| 图 3 极移序列ARMA模型诊断 Fig.3 Diagnostic of ARMA Model for PM |
因极移序列ARMA模型与ARIMA模型在Ljung-Box检验中具有高度的一致性,所以在这里只给出了ARMA模型的诊断展示。
本次选用的各个模型在上述检验中表现均良好,表明用于拟合极移X、Y分量的模型均能够非常好地捕获极移时间序列的相关结构。
2 模型预测与评价基于R语言和最小化的均方预测误差原理[9],根据拟合的模型分别对极移X、Y分量做出了预测。为验证所建立模型的短期预报精度,特留下了所采用数据2018-10-01-2018-11-14该段时间内的由IERS公布的实测极移数据以对所预测的模型进行评估,比较结果如图 4和图 5所示。
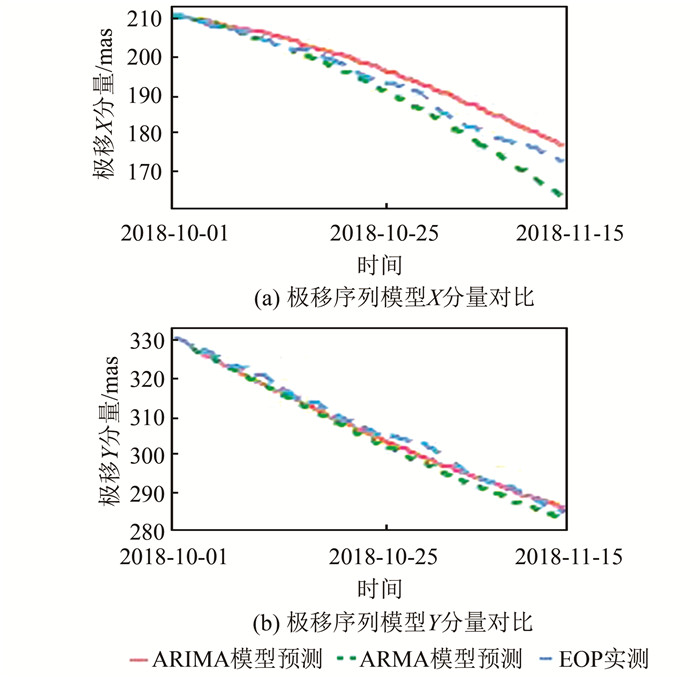 |
| 图 4 极移序列模型预测与实际值对比 Fig.4 Comparison of Predicted and Actual Values of the Model of Polar Motion |
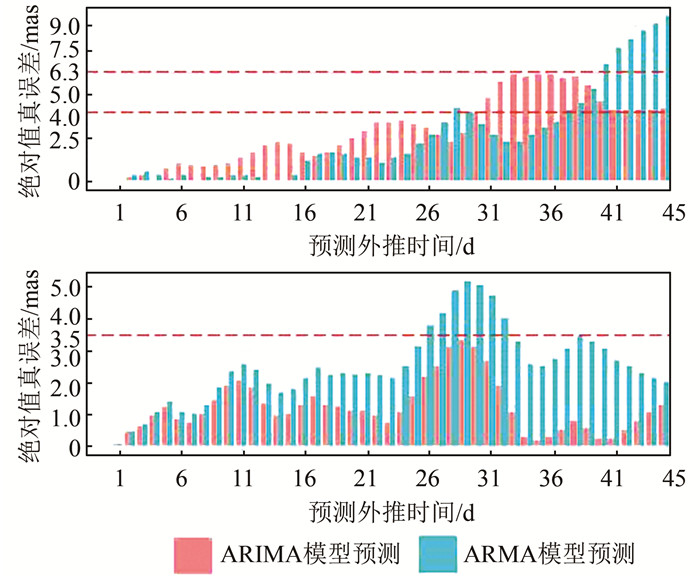 |
| 图 5 极移模型预测误差 Fig.5 Prediction Error of Polar Motion Mode |
由图 4和图 5可知:30 d内极移X分量ARIMA(2, 1, 8)模型的预测真误差均未超过±4 mas,ARMA(2, 8)模型在预测时间跨度36 d内,第28天和第29天的预测真误差超过了±4 mas,预测值分别为-4.23 052 617 mas和-4.019 864 331 mas。虽然在预测外推时间39 d内,ARMA(2, 8)模型在第27、28、29天的预测误差略大于ARIMA(2, 1, 8)模型,但ARMA(2, 8)模型的预测结果整体精度优于ARIMA(2, 1, 8)模型,故ARMA(2, 8)模型更适用于的1~35 d极移X分量的短期预报。极移Y分量ARMA(2, 9)模型在10 d预报跨度内精度较稳定,但45 d内预测真误差起伏较大;而ARIMA(2, 1, 7)模型预测真误差起伏较平缓。ARIMA(2, 1, 7)模型预测的精度明显优于ARMA(2, 9)模型,其预测真误差均未超过±3.5 mas,表明一阶差分能够有效提高极移Y分量的预测精度,所以ARIMA(2, 1, 7)模型更适用于极移Y分量的预测。与IERS测定的EOP精度以及文献[3-7]中的预报精度相对比,均验证了本文所拟合的极移时间序列模型的合理性以及应用到实际工作中的可行性。
3 结束语本文对极移X、Y分量分别进行了ARMA及ARIMA模型建模,并最终证明了在极移X分量短期预报中ARMA模型拟合优度更好、预测精度更高,而ARIMA模型通过差分处理更能捕获极移Y分量的变化趋势,提升了整体的预测精度。通过与其他拟合预报方法[3-7, 10, 11]对比,验证了本文模型在极移短期预报中的有效性。
| [1] |
李征航, 魏二虎, 王正涛, 等. 空间大地测量学[M]. 武汉: 武汉大学出版社, 2010.
|
| [2] |
Wei E H, Jin S G, Zhang Q, et al. Autonomous Navigation of Mars Probeusing X-Ray Pulsars: Modeling and Results[J]. Advances in Space Research, 2013, 51(5): 849-857. DOI:10.1016/j.asr.2012.10.009 |
| [3] |
魏二虎, 李智强, 龚光裕, 等. 极移时间序列模型的拟合与预测[J]. 武汉大学学报·信息科学版, 2013, 38(12): 1420-1424. |
| [4] |
魏晓蓓. 地球自转参数极移的预报方法研究[D]. 青岛: 山东科技大学, 2017
|
| [5] |
Shen Y, Guo J Y, Liu X, et al. One Hybrid Model Combining Singular Spectrum Analysis and LS+ARMA for Polar Motion Prediction[J]. Advances in Space Research, 2017, 59: 513-523. DOI:10.1016/j.asr.2016.10.023 |
| [6] |
Liao D C, Wang Q J, Zhou Y H, et al. Long-Term Prediction of the Earth Orientation Parameters by the Artificial Neural Network Technique[J]. Journal of Geodynamics, 2012, 62: 87-92. DOI:10.1016/j.jog.2011.12.004 |
| [7] |
王琪洁. 基于神经网络技术的地球自转变化预报[D]. 上海: 中国科学院研究生院(上海天文台), 2007
|
| [8] |
克莱尔. 时间序列分析及应用: R语言[M]. 潘红宇, 译. 北京: 机械工业出版社, 2011
|
| [9] |
崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差: 第4版[M]. 武汉: 武汉大学出版社, 2009.
|
| [10] |
李小军, 董翠军, 蔡顺中. 基于差分序列分析极移不规则变化及对模型拟合的影响[J]. 测绘地理信息, 2017, 42(1): 38-41. |
| [11] |
魏二虎, 杨亚利, 金双根, 等. 利用LS_AR模型对极移参数的中长期预报[J]. 测绘地理信息, 2014, 39(4): 5-9. |
 2021, Vol. 46
2021, Vol. 46

