| 地铁轨道控制网网形设计及模拟计算分析 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079;
3. 中铁工程设计咨询集团有限公司,北京,100055
2. Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China;
3. China Railway Engineering Consulting Group Co., Ltd., Beijing 100055, China
随着城市轨道交通的建设,引入高铁CPⅢ技术的地铁轨道控制网在地铁工程测量中的应用越来越多[1, 2]。高铁CPⅢ网按50~60 m的纵向间距成对布设CPⅢ点,采用自由设站边角后方交会网形进行测量,平面约束平差后点位中误差小于等于±2 mm,相邻点相对中误差小于等于±1 mm[3]。地铁轨道控制网在实际应用时,一方面布网时没有考虑到小曲线半径的隧道对观测视线的遮挡影响,只提出控制点间距为30~60 m[1]或直线段50 m、曲线段40 m[2];另一方面,测量数据平差计算后的精度指标还是以高铁CPⅢ网的为准。实际上,地铁轨道控制网与高铁CPⅢ网相比有很大不同,地铁轨道具有曲线半径小、测量起算数据精度低等特点[4]。本文结合地铁线路的特点,设计了合理的地铁轨道控制网的网形,通过模拟计算出地铁轨道控制网的点位中误差及相邻点相对中误差的合理精度指标。
1 地铁轨道控制网的网形设计地铁线路通常在地下隧道内,两个车站之间大多是单线圆形隧道,隧道横截面的一侧是应急通道,另一侧是消防水管,采用自由测站边角交会法对地铁轨道控制网进行外业测量时,实际能够架设全站仪的地方只有线路中线附近[5]。和高铁CPⅢ点类似,地铁轨道控制网的控制点在隧道壁两侧成对布设,相邻控制点的横向间距与隧道衬砌的内径有关。地铁线路受限于城市已有建筑,并顾及受惠区域,一般曲线段较多且半径较小,自由测站观测控制点时,视线受到地铁隧道壁的遮挡影响,在曲线段主要是接近曲线圆心一侧的隧道壁的遮挡,因此地铁轨道控制网的相邻控制点的纵向间距受到地铁隧道内测站的通视距离的限制。
如图 1所示,地铁隧道曲线圆心为O,轨道半径为R,圆隧道半径为r,在地铁隧道中间设站Z,观测视线极限是隧道壁的切点Q,Z到Q的长度即是通视距离S为:
| $ S = \sqrt {{R^2}-\left( {R-r} \right){\;^2}} \; = \sqrt {2Rr-{r^2}} $ | (1) |
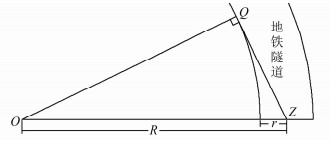 |
| 图 1 地铁隧道内测站的通视距离示意图 Figure 1 Sketch Map of Visible Distance of Station in Metro Tunnel |
轨道曲线半径和圆隧道半径各不相同的地铁隧道中,测站的通视距离也不同。《地铁设计规范》中要求,地铁轨道正线平面曲线最小半径在一般情况下,A型车是350 m,B型车为300 m;困难情况下,A型车是300 m,B型车为250 m。《地铁设计规范》中列举的正线平面曲线半径在600 m内每50 m递增,在800 m内每100 m递增,在1 200 m内每200 m递增,在1 500 m内每300 m递增,在3 000 m内每500 m递增。国内地铁单线圆形隧道的直径一般是5 m或6 m,本文研究时将直径取为6 m。根据式(1)计算隧道半径r=3 m时,各个不同曲线半径R下的通视距离结果如表 1所示。
| 表 1 不同曲线半径的通视距离和控制点纵向间距最大值/m Table 1 Visible Distances and Maximum Longitudinal Distance Between Two Control Points of Different Curve Radius/m |
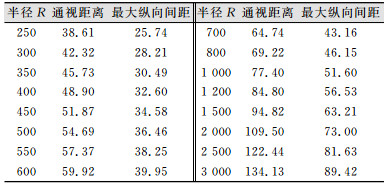 |
地铁轨道控制网外业测量时,如果每个自由测站观测前后各两对共4对(8个)控制点,那么控制点最大纵向间距大致是通视距离的2/3。根据表 1中的通视距离,计算不同曲线半径R下的控制点纵向间距最大值,结果见表 1。
从表 1可以看出,高铁CPⅢ网的50~60 m的纵向间距在地铁的小半径曲线隧道中显然无法满足,参照表 1的计算结果可知,地铁轨道控制网控制点合适的纵向间距是26~60 m。
高铁CPⅢ是以每个自由设站观测6对点,搬站时每次前进2个纵向间距的网形结构为主,而在地铁中受小半径曲线短通视距离的影响,小半径曲线处单站只能观测到4对点,搬站时也只能前进1个纵向间距,为使整个网形结构保持一致,合理的地铁轨道控制网的网形应如图 2所示。
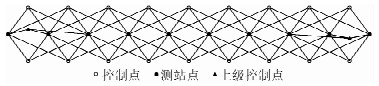 |
| 图 2 地铁轨道控制网模拟网形示意图 Figure 2 Sketch Map of Metro Track Control Network |
2 地铁轨道控制网平差计算模型
控制点纵向间距在曲线段各不相同的地铁轨道控制网采用不同标称精度的仪器测量时,其点位中误差和相邻点相对中误差精度如何?本文根据地铁轨道控制网的网形模拟外业测量时的观测值,依据间接平差模型对其进行约束平差计算,平差计算时给出水平方向和距离观测值的先验精度,根据Helmert方差分量估计方法对两种观测值进行验后估计,达到合理定权和改善网平差结果的目的。
2.1 间接平差模型与方差分量估计地铁轨道控制网的平面网的观测值是水平方向和距离,采用间接平差模型时,用V表示观测值的残差,B表示误差方程的系数,X表示未知点的坐标平差值,L表示常数项,组成误差方程为[6]:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{BX}}-\mathit{\boldsymbol{L}}\; $ | (2) |
其水平方向和距离的误差方程具体公式为:
| $ \left\{ \begin{array}{l} {v_{{L_{jk}}}} = \frac{{\rho \Delta Y_{jk}^0}}{{{{\left( {S_{jk}^0} \right)}^2}}}{{\hat x}_j}-\frac{{\rho \Delta X_{jk}^0}}{{{{\left( {S_{jk}^0} \right)}^2}}}{{\hat y}_j}-\frac{{\rho \Delta Y_{jk}^0}}{{{{\left( {S_{jk}^0} \right)}^2}}}{{\hat x}_k} + \\ \;\;\;\;\;\;\;\;\;\frac{{\rho \Delta X_{jk}^0}}{{{{\left( {S_{jk}^0} \right)}^2}}}{{\hat y}_k}-{{\hat z}_j} - {l_{jk}}\\ {v_{{S_{jk}}}} = - \frac{{\Delta X_{jk}^0}}{{S_{jk}^0}}{{\hat x}_j} - \frac{{\Delta Y_{jk}^0}}{{S_{jk}^0}}{{\hat y}_j} + \frac{{\Delta X_{jk}^0}}{{S_{jk}^0}}{{\hat x}_k} + \\ \;\;\;\;\;\;\;\;\;\;\frac{{\Delta Y_{jk}^0}}{{S_{jk}^0}}{{\hat y}_k} - {l_{jk}} \end{array} \right. $ | (3) |
式中,ρ是弧度制与角度制转换的常数;j表示测站点;k表示控制点;$\hat x$和$\hat y$是未知点坐标改正数;ΔXjk0和ΔYjk0是坐标增量的近似值;Sjk0是水平距离的近似值;${\hat z_j}$是测站的定向角改正数;ljk是水平方向或距离的误差方程常数项。
地铁轨道控制网中有两类不同类型的观测值,以全站仪标称的水平方向观测值的中误差mL作为先验单位权中误差,即σ0=mL,按照经验定权法确定水平方向和距离观测值的初始权比关系为[6]:
| $ \left\{ \begin{array}{l} {P_{{L_{jk}}}} = \frac{{{\sigma _0}^2}}{{{m_{{L_{jk}}}}^2}}\\ {P_{{S_{jk}}}} = \frac{{{\sigma _0}^2}}{{{m_{{S_{jk}}}}^2}} = \frac{{{m_L}^2}}{{{{\left( {a + b\;{S_{jk}}} \right)}^2}}} \end{array} \right. $ | (4) |
式中,a和b分别是全站仪标称的测距固定误差和比例误差。
用P表示观测值的权,根据方程式(2)和式(4),依据最小二乘原理组成法方程[6]为:
| $ {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PBX}}{\rm{-}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}}{\rm{ = 0}} $ | (5) |
约束平差是将上级控制点作为已知点,对测站点和控制点的坐标在上级控制网坐标系下进行求解。由于上级控制点已知,法方程式(5)中的系数可逆,可得未知点的坐标平差值X和其坐标协因数阵Q分别为[6]:
| $ \mathit{\boldsymbol{X = }}{\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{-1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}} $ | (6) |
| $ \mathit{\boldsymbol{Q = }}{\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{-1}} $ | (7) |
观测值的权对控制网的平差结果影响重大,进行平差计算时,若是仅以全站仪的标称精度估算水平方向和距离观测值的方差并定权,这在地铁轨道控制网这种高精度控制测量的情况下是不够精确的。本文先对地铁轨道控制网的水平方向和距离两种观测值赋予初始权进行预平差,然后利用两种观测值的改正数平方和对相应的验后方差做出估计,接着重新赋予权值并重新平差计算,不断迭代计算,直到两种观测值的单位权方差估值相等或接近一致,达到求得最优估值的目的。Helmert方差分量估计求得的单位权方差为[7]:
| $ \begin{array}{l} \left[\begin{array}{l} \sigma _1^2\\ \sigma _2^2 \end{array} \right] = {\left[\begin{array}{l} {n_1}-2{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{-1}}\;{\mathit{\boldsymbol{N}}_{\rm{1}}}} \right) + {\rm{tr}}{\left( {{\mathit{\boldsymbol{N}}^{-1}}\;{\mathit{\boldsymbol{N}}_{\rm{1}}}} \right)^2}\;\;\;\;\;\;{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}\;{\mathit{\boldsymbol{N}}_{\rm{1}}}\;{\mathit{\boldsymbol{N}}^{ - 1}}\;{\mathit{\boldsymbol{N}}_2}} \right)\\ \;\;\;\;\;{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}\;{\mathit{\boldsymbol{N}}_{\rm{1}}}\;{\mathit{\boldsymbol{N}}^{ - 1}}\;{\mathit{\boldsymbol{N}}_2}} \right)\;\;\;\;\;\;\;\;{n_2} - 2{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}\;{\mathit{\boldsymbol{N}}_2}} \right) + {\rm{tr}}{\left( {{\mathit{\boldsymbol{N}}^{ - 1}}\;{\mathit{\boldsymbol{N}}_2}} \right)^2} \end{array} \right]^{ - 1}}\\ \left[\begin{array}{l} \mathit{\boldsymbol{V}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{1}}}{\mathit{\boldsymbol{V}}_{\rm{1}}}\\ \mathit{\boldsymbol{V}}_2^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{2}}}{\mathit{\boldsymbol{V}}_{\rm{2}}} \end{array} \right] \end{array} $ | (8) |
式中,σ12和σ22分别是水平方向和距离观测值的验后单位权方差;n1和n2分别是两种观测值的数目;N1= B1TP1B1和N2= B2TP2B2分别是两种观测值的法方程系数阵, B1和B2分别是两种观测值的误差方程系数阵,P1和P2分别是两种观测值的权值;V1TP1V1和 V2TP2V2分别是两种观测值的残差平方和;N = BTPB是整网法方程的系数阵;tr(*)是矩阵求迹。
2.2 点位中误差和相邻点相对点位中误差计算Helmert方差分量估计结束后,将式(6)代入式(2),即可得到地铁轨道控制网约束平差后的观测值残差V。对于点位中误差和相邻点相对中误差,需要先计算后验单位权中误差为[6]:
| $ {\sigma _0} = \sqrt {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV/}}\mathit{r}} $ | (9) |
式中,r=n-2m-s是地铁轨道控制网的多余观测数,其中n是观测值总数;m是未知点总数;s是测站数。
地铁轨道控制网中,未知点的横纵坐标中误差和点位中误差为[6]:
| $ \left\{ \begin{array}{l} {m_X} = {\sigma _0}\;\sqrt {{Q_{XX}}} \\ {m_Y} = {\sigma _0}\;\sqrt {{Q_{YY}}} \\ {m_P} = {\sigma _0}\;\sqrt {{Q_{XX}} + {Q_{YY}}} \end{array} \right. $ | (10) |
式中,QXX和QYY可以在式(7)的坐标协因数阵Q中找到。
对于相邻点相对中误差,需要相邻两点的相对位置。在地铁轨道控制网中,相邻两点A(xA,yA)和B(xB,yB)的相对位置可以用坐标增量表示为:
| $ \left\{ \begin{array}{l} \Delta {X_{AB}} = {X_B}-{X_A}\\ \Delta {Y_{AB}} = {Y_B}-{Y_A} \end{array} \right. $ | (11) |
对式(11)运用协因数传播率,可得相邻两点的坐标增量的互协因数为[6]:
| $ \left\{ \begin{array}{l} {Q_{\Delta X\Delta X}} = {Q_{{X_B}{X_B}}} + {Q_{{X_A}{X_A}}}-2{Q_{{X_B}}}_{{X_A}}\\ {Q_{\Delta Y\Delta Y}} = {Q_{{Y_B}{Y_B}}} + {Q_{{Y_A}{Y_A}}}-2{Q_{{Y_B}}}_{{Y_A}} \end{array} \right. $ | (12) |
式中,等号右侧的各项都可在式(7)的坐标协因数阵Q中找到。
地铁轨道控制网中,相邻两点的横纵坐标相对中误差和相对点位中误差为:
| $ \left\{ \begin{array}{l} {m_{\Delta X}} = {\sigma _0}\;\sqrt {{Q_{\Delta X\Delta X}}} \\ {m_{\Delta Y}} = {\sigma _0}\;\sqrt {{Q_{\Delta Y\Delta Y}}} \\ {m_{\Delta P}} = {\sigma _0}\;\sqrt {{Q_{\Delta X\Delta X}} + {Q_{\Delta Y\Delta Y}}} \end{array} \right. $ | (13) |
取地铁轨道控制网控制点的横向间距为6 m,对于表 1中地铁轨道不同的曲线半径,本文取250 m、350 m和800 m及800 m以上的半径进行模拟计算,相应的控制点纵向间距分别为25.5 m、30 m、46 m和60 m。高铁CPⅢ网要求每600 m左右联测一个上级控制点[3],按照图 2的示意网形,分别以上述4种纵向间距在AutoCAD中设计总长约600 m的地铁轨道控制网。同时,考虑到地铁隧道的特点,地铁车站处一般比较稳定且有地面传入的高等级控制点,按一般地铁车站1 000 m的间隔,在AutoCAD中设计总长约1 000 m的地铁轨道控制网[8]。
使用Matlab的normrnd函数,模拟服从(0, 1)正态分布的随机数序列,根据控制点、测站点的设计坐标和每个测站的观测方案,反算水平方向和距离的观测值,并给观测值添加由相应先验精度乘以随机数得到的随机误差,形成模拟观测值。关于先验观测精度,本文取仪器的标称精度,徕卡全站仪常见的TCA2003或TS30的标称精度为0.5″、1 mm+1×10-6,TCA1800或TCA1201的标称精度是1″、1 mm+2×10-6,TS02或TS06的标称精度为2″、1.5 mm+2×10-6。
高铁CPⅢ点标志安装重复性和互换性安装误差有0.4 mm的限差[3],考虑到实际地铁轨道控制网外业测量时,控制点上安装棱镜同样有重复性和互换性安装误差,本文取限差的1/2作为中误差,即±0.2 mm。根据控制点坐标反算观测值之前,给控制点的设计坐标添加0.2 mm乘以随机数得到的随机误差,用以模拟地铁轨道控制网测量时的棱镜重复性和互换性安装误差。
对上述地铁轨道控制网的模拟观测值进行Helmert方差分量估计平差计算,来评定地铁轨道控制网的精度。
3.2 后验单位权中误差对比分析模拟观测值添加服从正态分布的随机误差,为了评价其实际精度情况,用§3.1中的3种仪器标称精度,以不同的控制点纵向间距,按不考虑控制点棱镜重复性和互换性安装误差的模式模拟观测值,进行Helmert方差分量估计平差计算,统计各种情况下的后验单位权中误差,结果如表 2所示。由表 2中的数据可知,所有网形的后验单位权中误差均与模拟时给定的先验标称精度相近,而后验单位权中误差是采用Helmert方差分量估计方法估算出来的观测值的实际观测精度,先验精度与后验精度一致性好,表明观测值模拟计算方法正确。
| 表 2 考虑棱镜安装误差与否的后验单位权中误差/(″) Table 2 Unit Weight Mean Error Considering the Prism Installation Error or Not/(″) |
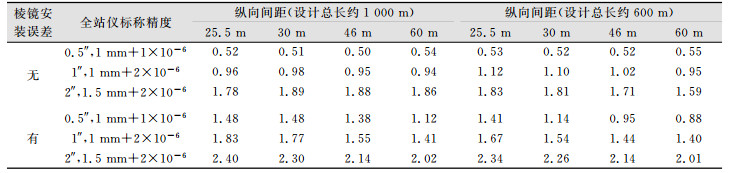 |
为考察控制点棱镜重复性和互换性安装误差对地铁轨道控制网精度的影响,特在模拟观测值时考虑测点的重复性和互换性安装误差,由表 2中的数据可知:①因引入了棱镜的重复性和互换性安装误差,所有网形的后验单位权中误差均比模拟时给定的先验标称精度要大;②同样的棱镜重复性和互换性安装误差,网点纵向间距越短,对整个控制网的实际测角精度(后验单位权中误差)影响越大。
由以上的比较分析可知,本文使用的观测值模拟计算方法正确,结果可靠。控制点棱镜重复性和互换性安装误差对控制网的实际测角精度有显著影响,因此,在模拟评价地铁轨道控制网的精度时,应考虑引入棱镜重复性和互换性安装误差。
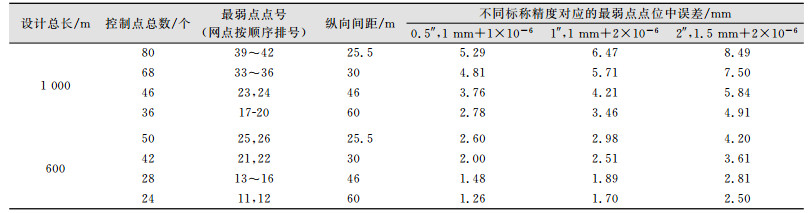
3.3 点位中误差和相邻点相对点位中误差按照图 2的网形结构,分别以25.5 m、30 m、46 m和60 m的控制点纵向间距,引入棱镜重复性和互换性安装误差,设计总长约1 000 m和约600 m的地铁轨道控制网,且在网形两端引入已知的上级控制点,采用Helmert方差分量估计方法对设计网形的模拟观测值进行约束平差计算,分别统计最弱点点位中误差和相邻点相对点位中误差,结果如表 3和表 4所示。
| 表 3 考虑棱镜安装误差的最弱点点位中误差 Table 3 Most Weakness Position Accuracy Considering the Prism Installation Error |
 |
| 表 4 考虑棱镜安装误差的相邻点相对点位中误差最大值/mm Table 4 Relative Position Accuracy of Two Points Considering the Prism Installation Error/mm |
 |
由表 3可知:①在地铁轨道控制网总长相同的情况下,网点纵向间距越短,最弱点点位中误差越大;②对两端引入已知点进行约束的网形,总长较短的地铁轨道控制网,其最弱点点位中误差较小;③按高铁CPⅢ网50~60 m的点对间距,每600 m左右联测一个上级控制点,采用测角标称精度1″以上的全站仪观测,最弱点点位中误差可达到高铁规范要求的优于±2 mm;④对地铁网而言,26~60 m的点对间距,每1 000 m左右在车站处联测一个上级控制点,最弱点点位中误差显然达不到优于±2 mm的要求,综合考虑,采用测角标称精度1″以上的全站仪观测,最弱点点位中误差定为优于±5 mm较为合适,且布网时应注意尽量减少短的点对间距出现的数量。
表 4中的最大值统计的是式(13)中的mΔP,剔除了设计网形中横纵坐标与坐标轴大致平行的影响,且只对图 2网形的第5点与倒数第5点之间的相邻点相对点位中误差进行统计,剔除了开网收网的影响。由表 4中的数据可知:①与点位中误差相反,网点纵向间距越短,相邻点相对点位中误差越小;②对两端引入已知点进行约束的网形,总长较短的网形,相邻点相对点位中误差较小;③采用测角标称精度1″以上的全站仪,两种总长的地铁轨道控制网的相邻点相对点位中误差优于±1 mm。
4 结束语本文根据地铁隧道曲线段的不同曲线半径,设计了地铁轨道控制网的控制点纵向间距,并进行了计算和分析,得出如下结论:①受地铁小半径曲线的影响,地铁轨道控制网应采用单站观测4对点,搬站时前进1个纵向间距较为合理;②地铁轨道控制网的合理纵向间距为26~60 m;③地铁轨道控制网的控制点棱镜重复性和互换性安装误差对控制网的实际测角精度有显著影响,控制网的实际测角精度达不到采用的测量仪器的标称精度;④地铁轨道控制网应采用测角标称精度1″以上的全站仪进行观测;⑤每1 000 m左右在车站处联测一个上级控制点的地铁轨道控制网,最弱点点位中误差指标定为优于±5 mm较为合适;⑥地铁轨道控制网的相邻点相对中误差指标可定为优于±1 mm。
| [1] | 秦政国, 陶利, 王丰林. 高铁CPⅢ技术在地铁铺轨工程中的应用与分析[J]. 现代测绘, 2013, 36(1): 16–18 |
| [2] | 孟峰, 马全明, 陈大勇, 等. CPⅢ控制网测量技术在城市轨道交通中的应用研究[J]. 测绘通报, 2013, (1): 73–76 |
| [3] |
中华人民共和国铁道部. 高速铁路工程测量规范: TB 10601-2009 [S]. 北京: 中国铁道出版社, 2009 |
| [4] | 刘永中. CPⅢ控制网测量技术在地铁轨道测量中的应用探讨[J]. 现代城市轨道交通, 2014, (1): 95–98 |
| [5] |
北京城建设计研究总院. 地铁设计规范: GB 50157-2013[S]. 北京: 中国计划出版社, 2013 |
| [6] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2003 |
| [7] |
耿文燕. 无砟轨道CPⅢ控制网精算方法及数据处理研究[D]. 兰州: 兰州交通大学, 2014 |
| [8] | 刘成龙, 杨友涛, 徐小左. 高速铁路CPⅢ交会网必要测量精度的仿真计算[J]. 西南交通大学学报, 2008, 43(6): 718–723 |
 2018, Vol. 43
2018, Vol. 43

