| 基于自适应K值选择的K近邻算法研究 |
2. 中国矿业大学环境与测绘学院,江苏 徐州, 221116
2. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China
随着物联网应用的不断扩大和深入,LBS (location based services)越来越重要。现有的定位技术有美国的全球定位系统(global positioning system, GPS)、俄罗斯卫星导航系统(global navigation satellite system, GLONASS),也有逐步建成和投入使用的北斗卫星导航系统(BeiDou navigation satellite system, BDS)和欧盟伽利略卫星导航系统(Galileo positioning system)。然而由于受到建筑物本身的遮挡以及建筑物内部结构的影响,卫星导航定位无法应用于室内环境。随着无线局域网(wireless loc al area networks, WLAN)的普及,基于RSSI (received signal strength indication)的室内定位方法[1]因无需添加额外硬件设备而具有广泛的应用价值。
基于RSSI的室内定位方法分为离线训练和在线定位两个阶段,离线训练阶段构建指纹库,在线定位阶段利用实时接收RSS (received signal strength)信号与指纹库进行指纹匹配。在离线阶段,通过指纹库信号预处理能够得到稳定的信号强度值,但在定位阶段,为获取稳定信号强度值则需要延长接受RSS信号的时间[2],这并不符合LBS的需求。为提高定位精度和定位实时性,需要引用聚类技术[3, 4],并深入挖掘WLAN信号的特性。在提高实时性方面引入聚类思想可缩减定位时间。在WLAN信号特征挖掘上,研究发现WLAN信号受到干涉、反射、多径效应和遮挡等的影响,依据WLAN信号的影响因素,为使RSS能够较准确地反映接收信号强度与物理位置之间的关系,常用的方式是AP (access point)选择算法,该方式从Youssef等人的MaxMean[5]方法到基于信息增益的InfoGain算法[6],再到郑志安的联合AP算法[7]。另一种方式是RSS值预处理的方法,代表算法有尺度不变特征变换[8]、梯度方向直方图[9]、核主成分分析[10]、核线性判别分析[11]。以上两种方式深入挖掘了信号特性,并取得了较好的成果,但是AP选择算法和RSS值预处理的研究重点均涉及在线阶段的测试点间的信号特征及其空间关系特征。
本文针对K近邻(K nearest neighbor, KNN)算法采用固态K值无法得到最优定位的问题,利用测试点间的信号特征及其空间关系特征,依据室内AP的几何布局特征划分矢量域,并利用测试点信号特征序列[12]来识别每个矢量域,进而实现区域改正,选取最优的K值。试验结果表明,该算法在时效性和定位精度上均有所提高。
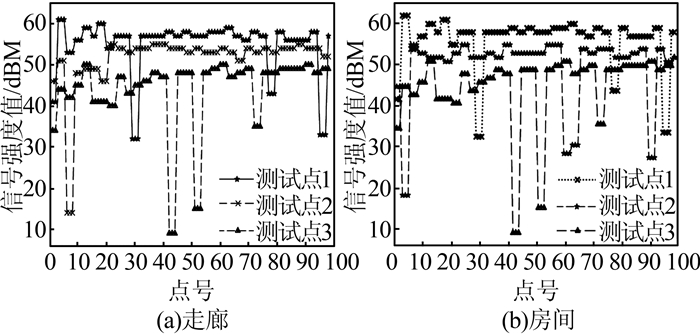
1 自适应K值选择的KNN算法 1.1 相邻时空信号特性分析WLAN信号强度随着时间和空间变化而随机变化。本文着重研究了短时间和短距离间隔内信号强度的波动性特征,即相邻时间和相邻空间信号强度波动性。本文在狭长的走廊和复杂的房间内分别取相距0.6 m、1.2 m、1.8 m的测试点以2 Hz的频率在50 s内采集的100个样本点进行统计,并对某一AP的信号强度进行统计分析,如图 1所示。
 |
| 图 1 相邻空间信号强度波动性 Figure 1 Volatility of Adjacent Space Signal Strength |
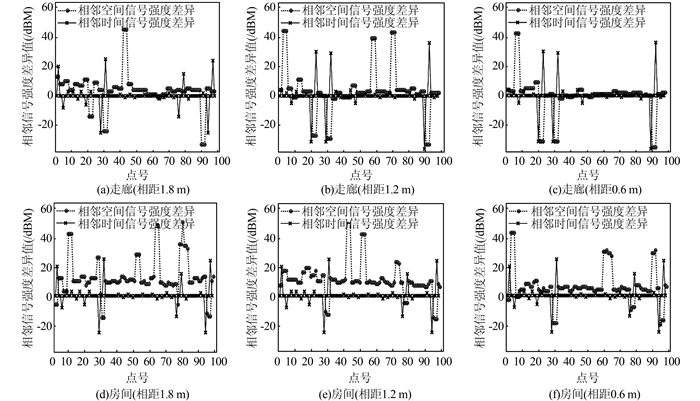
由图 1知,测试点之间的信号强度具有明显的差异,且随距离单调变化。由试验条件分析发现,造成测试点间信号强度差异的因素主要为空间距离的变化和随机噪声。对同一固定AP点的相邻空间和时间的信号强度差异进行统计,如图 2所示。相邻空间信号强度差异是指两相邻位置的同一无线设备的接受信号强度差分后的序列,相邻时间信号强度差异是指同一位置的相邻时间间隔的同一无线设备的接收信号差分后的序列。
 |
| 图 2 相邻空间和时间信号强度差异 Figure 2 Volatility of Adjacent Space and Time Signal Strength |
在走廊和房间两种室内结构体内,相邻时间信号强度差异值除少数突变情况外,均匀分布在0值附近。相邻空间信号差异值则大于相邻时间信号强度差异值,且该差异值随空间距离的增大而增大。同时,相邻空间信号差异值随室内结构体环境的复杂程度而变化,且结构体环境越复杂,相邻空间信号差异值越大。由图 2可知,房间内相邻空间信号差异值大于走廊。故在短时间间隔内的连续定位点间信号强度差异主要受空间距离变化的影响。基于以上分析,通过利用相邻两测试点间信号强度的增减,判断测试点与固定AP点之间的距离变化,进而推测出测试点间的空间关系。为精确提取两测试点间相邻空间变化因素的影响,需在测试点间的差异性中消除随机噪声的影响,本文根据图 2统计结果取均值为0、方差为1的随机数来消除其影响。
1.2 自适应K值选择在KNN算法中,最邻近样本点选择的准确性依赖于K值的选择,如果K值选择太小,那么被选择的最邻近样本点随之减少,若样本点的选择存在误差,那么会造成较大的定位误差;如果K值选择过大,在增加算法定位开销的同时,更容易引入许多距离较远的样本点,同样也会导致定位误差增大[13]。通过利用距离是短时间内造成信号强度波动的主导因素这一特征,自适应选择K值,从而获得最优定位效果。
由于两相邻测试点之间在时空上具有连续性,并且时间间隔较短,两测试点间信号的波动性主要来源于距离因素和信号的随机波动影响,并且距离因素占主导地位。但是当测试点处存在遮挡或某时刻的随机波动性较大,距离因素变为次要因素时,相邻测试点间信号强度差异值均为负值,则忽略此点。此外,以各测试点为中心构建4个矩形区域,区域边长为一定时间间隔内的最大行走距离,并将4个方格所构成的正方形区域以对角线为基准划分为8份。然后以相邻测试点间的信号强度差异为依据判定另一测试点的定位估计区域,从而得到两测试点之间的空间关系。
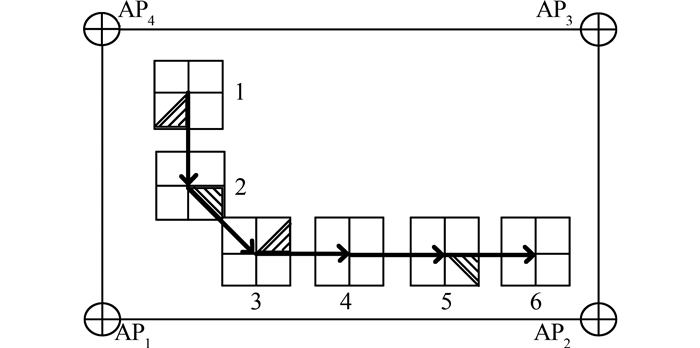
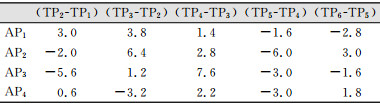
在试验场范围内选取6个测试点(test point,TP),并在6个测试点中选取4个接收信号强度最大的点(AP),如图 3所示。从相邻空间和时间信号强度波动性特征可知,距离是短时间内造成信号强度波动的主导因素。利用相邻测试点间的空间信号波动特征,通过两测试点TP与固定点AP之间的距离远近关系,来判断两测试点间的空间关系,如表 1所示。
 |
| 图 3 运动趋势判定 Figure 3 Determination of Moving Trend |
| 表 1 相邻测试点间信号强度差异 Table 1 Difference of Single Strength Between Adjacent Points |
 |
由相邻两测试点的定位结果的空间位置关系构建的矢量称之为空间矢量,本文取K为1、2、3和4,可得6种不同K值的定位结果组合的空间矢量ΩKiKj。依据上文分析,由RSS信号强度差异值可得如图 3的该相邻测试点的另一空间矢量Ωrssij。通过计算ΩKiKj与Ω rssij间的夹角,当空间矢量间夹角越小,定位结果与实际运动趋势越近似。通过以上匹配,选出最相近的一组,并以该组K值的KNN定位结果作为最终的定位结果,为:
| $\begin{align} & {{\boldsymbol{\Omega} }_{{{K}_{i}}{{K}_{j}}}}=\Lambda \left( \left\langle {{\Omega }_{{{K}_{i}}{{K}_{j}}}},{{\boldsymbol{\Omega} }_{\text{rs}{{\text{s}}_{i}}_{j}}} \right\rangle \right)\in \\ & \left( {{K}_{i}}=1,2,3,4;{{K}_{j}}=1,2,3,4 \right) \\ \end{align}$ | (1) |
式中,ΩKiKj表示两相邻测试点采用KNN算法,K取Ki和Kj时定位结果构成的空间矢量; Ω rssij是由信号强度差异推断得到的两相邻测试点的空间矢量; Λ (〈, 〉)∈(Ki; Kj)指K值取Ki和Kj时,两种空间矢量的匹配运算,并取相似度最大的一组作为最终的定位结果。
从上述自适应K值选择的KNN算法描述中可知,在定位估计前,需已知各测试点在可视范围内的APs及其相对物理位置关系。故本文采用在测试点的可视范围内搜索3个或是4个AP构成矢量域,并尽量保证每个矢量域大小相近,以避免区域间判别的误差。
信号特征序列指抽象的、与物理层技术无关的、反映一个位置与多个位置间距离由近至远顺序关系的序列,所以信号特征序列中的AP的排序反映了测试点与各AP点之间的距离亲近程度。然而,随着距离的增加,各种影响因素的影响增大,导致序号特征序列与距离关系出现明显相悖的情况。故本文仅利用信号特征序列的前几位AP来识别测试点所在的矢量域。为提高矢量域判别准确率,在基于信号特征序列判定矢量域时,需考虑两种特殊情况。一是当矢量域内的AP位于测试点信号特征序列首位时,测试点与该AP点相近的可信度增大,故增大测试点在该矢量域的权重;二是当某一矢量域内的AP相对于其他矢量域均为不可视时,则在信号特征序列前几位出现该AP时,增大测试点在该矢量域的权重。此外,依据划定的矢量域范围,可对定位结果进行区域改正。通过试验验证,矢量域识别的准确率可达到96%。
1.3 K-means聚类指纹库考虑到KNN指纹定位方法所需的指纹数据库相对庞大,导致在进行数据库实时匹配过程中计算量较大。为提高定位实时性,引入K-means聚类对指纹库进行聚类分块处理,使实时匹配定位时只需与其中一个子类块进行匹配,而无需对整个指纹数据库全部逐一匹配。K-means聚类过程是一个不断循环的计算过程,直到所有采样点到相应中心的距离之和E收敛到最小为止:
| $E=\sum\limits_{i=1}^{k}{\sum\limits_{l\in {{C}_{i}}}{\left\| l-c{{c}_{i}} \right\|}}$ | (2) |
式中,l为参考点样本;Ci为第i族;cci为族Ci的平均值。
K-means聚类结果如图 4所示。
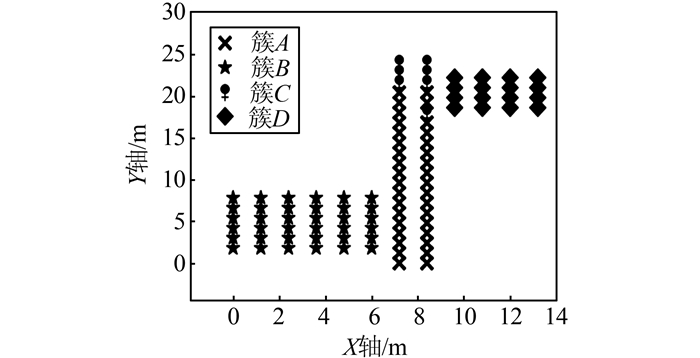 |
| 图 4 K-means聚类结果 Figure 4 Result of K-means Clustering |
2 试验结果与分析
基于WLAN建立试验场,试验场为中国矿业大学环测学院4楼的部分区域,包含实验室A409、走廊和乒乓球台。在试验场内布设1.2 m×1.2 m的94个规则格网控制点,并在A409、走廊和乒乓球台3个区域分别采集22个、19个和10个共51个测试点。根据试验场的AP点布局特征将试验场划分为A、B、C、D、E共5个矢量域,如图 5所示。
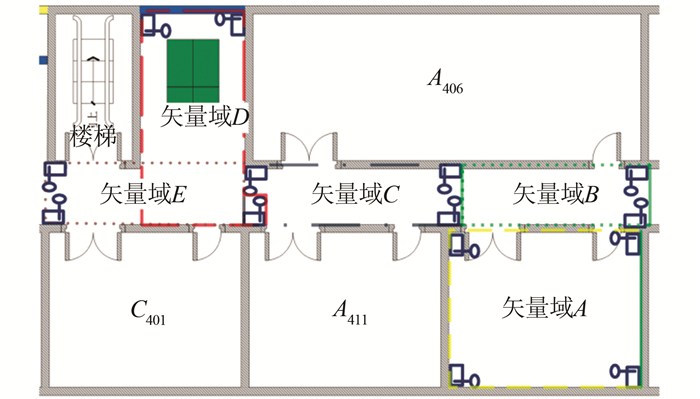 |
| 图 5 试验场内的矢量域分布 Figure 5 Distribution of Vector Fields in Experimental Area |
在线定位阶段采用以下3种定位算法完成定位估计。
1) 试验1。采用KNN算法,分别取K为1、2、3和4进行定位估计。
2) 试验2。采用基于聚类指纹库的K最邻近算法(based clustering fingerprint database-KNN, CKNN),并对定位结果依据聚类区域进行区域改正算法,分别取K为1、2、3和4进行定位估计。
3) 试验3。在试验2算法基础上加入自适应K值选择算法和基于矢量域的区域改正算法(adaptive selection K value and regional correction-KNN,ARCKNN)算法。根据上述试验方案得定位轨迹如图 6所示。
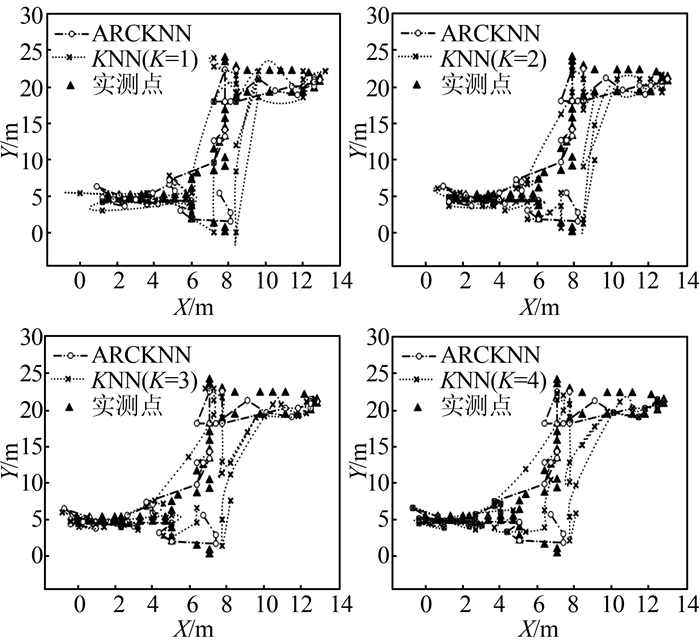 |
| 图 6 定位轨迹 Figure 6 Location Trajectories |
从图 6可以看出,ARCKNN算法的定位轨迹的鲁棒性明显优于KNN算法的任意K值,而且针对定位点的跳动问题也有了很明显的改善。另外,ARCKNN算法中依据划定的矢量域进行区域改正策略,可以将定位结果限定到正确的矢量域,从而克服了定位结果穿墙现象的发生。根据定位结果,利用均方根误差(RMSE)和时间来评价3种定位算法的定位效果,如表 2所示。
| 表 2 ARCKNN与CKNN、KNN定位效果对比 Table 2 Comparison of Location Efficiency of ARCKNN with CKNN and KNN |
 |
表 2结果表明,ARCKNN算法与CKNN和KNN算法相比,定位效果的综合性能有了一定的提升。在定位精度上,ARCKNN算法优于任意K值条件下的CKNN和KNN算法。K为3和2时分别为CKNN和KNN算法的最优定位效果,而ARCKNN算法相对于K为4时的CKNN算法均方根误差提高了0.1 m,相对于K为2时提高了2.2 m。ARCKNN算法在提高定位精度的同时,同样极大地改善了定位过程的实时性。尤其是相对于KNN算法,完成51个测试点定位所消耗的时间缩减了近7 s,而相对于CKNN算法,在提升定位精度的同时,所消耗的时间仅增加不到2 s。
3 结束语本文在深入挖掘测试点间的信号特征及其空间关系特征的基础上,提出了自适应K值选择的KNN算法,算法实现了KNN算法中K值的自适应选择和依据矢量域的区域改正。试验结果表明,该算法在定位精度上可达到1.5 m,在定位稳定性和实时性上也有明显的提升。但文中自适应选择的K值并未达到最优的定位效果,还有待进一步研究。
| [1] |
徐元坤. 基于Wi-Fi和Android平台的室内定位技术研究[J].
测绘地理信息,2014,39(5) : 21–24.
Xu Yuankun. Indoor Location Based on Wi-Fi and Android Platform[J]. Journal of Geomatics,2014,39(5) : 21–24. |
| [2] | Youssef M, Agrawala A. The Horus WLAN Location Determination System[C]. The 3rd International Conference on Mobile Systems, Applications and Services, Seattle, Washington, 2005 |
| [3] | Yousse F, Agrawala M A, Shankar A, et al.A Probabilistic Clustering-Based Indoor Location Determination System[R].Technical Reports of the Computer Science Department, Washington D C, USA, 2002 |
| [4] | Yousse F, Agrawala M A, Shankar A, et al.Location Determination Via Clustering and Probability Distributions[C].The First IEEE International Conference on Pervasive Computing and Communications, Forth Worth, Texas, USA, 2003 |
| [5] | Youssef M, Agrawala A. Handling Samples Correlation in the Horns System[C].IEEE Info Com 2003, San Franciso, USA, 2004 |
| [6] | Chen Y, Yang Q, Yin J, et al. Power-Efficient Access-Point Selection for Indoor Location Estimation[J]. IEEE Transactions on Knowledge and Data Engineering,2006,18(7) : 877–884. DOI:10.1109/TKDE.2006.112 |
| [7] |
郑志安.基于学习算法的WLAN室内定位技术研究[D].哈尔滨:哈尔滨工业大学, 2012 Zheng Zhian.Research on Learning Based WLAN Indoor Positioning Techniques[D]. Harbin :Harbin Institute of Technology, 2012 |
| [8] | Cruz M J, Bogdanova I, Paquier B, et al. Scale Invariant Feature Transform on the Sphere: Theory and Applications[J]. The International Journal of Computer Vision,2012,98(2) : 217–241. DOI:10.1007/s11263-011-0505-4 |
| [9] | Rybski P E, Huber D, Morris D D, et al.Visual Classification of Coarse Vehicle Orientation Using Histogram of Oriented Gradients Features[C].IEEE Conference on Intelligent Vehicles Symposium, New York, USA, 2010 |
| [10] | Wang J, Zhou Y S, Du X J, et al.Personal Credit Assessment Based on KPCA and SVM[C].International Conference on Business Intelligence and Financial Engineering, Beijing, China, 2012 |
| [11] | Zafeiriou S, Tzimiropoulos G, Petrou M, et al. Regularizad Kernel Discriminant Analysis with a Robust Ker nel for Face Recognition and Verification[J]. IEEE Transactions on Neural Networks and Learning Systems,2012,23(3) : 526–534. DOI:10.1109/TNNLS.2011.2182058 |
| [12] | Yedavalli K, Krishnamachari B. Sequenee-Based Localization in Wireless Sensor Networks[J]. IEEE Transactions on Mobile Computing,2008,7(1) : 81–94. DOI:10.1109/TMC.2008.4387797 |
| [13] |
陈永乐, 于丹, 王泽. 基于相似指纹特征的室内定位机制研究[J].
太原理工大学学报,2015,46(3) : 336–340.
Chen Yongle, Yu Dan, Wang Ze. Indoor Positioning Mechanism Research Based on Similar Fingerprint Characteristics[J]. Journal of Taiyuan University of Technology,2015,46(3) : 336–340. |
 2016, Vol. 41
2016, Vol. 41

