| UWB室内距离交会定位算法的研究与性能分析 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079;
3. 武汉大学灾害监测与防治研究中心,湖北 武汉,430079
2. The Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan University, Wuhan 430079, China;
3. Hazard Monitoring and Prevention Research Center, Wuhan University, Wuhan 430079, China
科技飞速发展的今天,人们对于位置服务的需求愈加强烈,在室外利用全球卫星导航系统(global navigation satellite system, GNSS)可以实时确定自己的位置。但由于室内环境的复杂性及障碍物的遮挡作用,无法利用GNSS技术获得高精度的室内定位结果[1, 2]。目前,室内定位技术主要有:蓝牙(bluetooth)定位技术、WiFi定位技术、ZigBee技术、超宽带技术(ultra-wideband, UWB)等。其中,UWB是一种在极大带宽上进行数据传输的无载波通信技术,具有高数据率、穿透力强等特点,能获得分米级的定位结果,是众多室内定位技术中较为重要的技术之一[3, 4]。
UWB技术在时域的高分辨率能力,为无线定位提供了一种极好的手段,其定位的基本机制包括:基于到达角度(angle of arrival, AOA)、基于到达时间(time of arrival, TOA)、基于到达时间差(time difference of arrival, TDOA)以及基于到达信号强度(received signal strength, RSS)[5]等。由此学者们提出了大量的UWB定位算法。如文献[6]提出Fang算法,通过线性化双曲线方程估计目标的位置,原理简单,能够得到基于距离差的最优解,在视距(line of sight, LOS)条件下定位精度较高,但无法通过冗余信息提高精度,易受随机误差影响;文献[7]提出Chan算法,通过导出最大似然(maximum likelihood,ML)方程,从而估计待测目标位置,在误差服从高斯分布时有良好的定位精度,计算量小,通过增加基站数量可以提高精度。但ML检测算法的复杂度随着发射天线数和调制阶数的增加呈现指数式增加[8]。距离交会定位算法简单、易于操作,对基站数量要求低,节省成本,是最常用的室内定位方法;但由于测距误差的存在,很难建立精准的、适于实际情况的损耗模型[9]。
TOA定位精度主要受时钟同步误差和时间的测量误差影响,要求基站与目标做到精确的时钟同步;TDOA定位以双曲线为模型,要求基站之间时钟同步;RSS定位需要知道信道衰弱模型,受多径影响极为严重;AOA定位要求基站必须装备方向敏感的天线阵列,角度值的极小偏差都能引起较大的定位误差。而距离交会定位不需要时钟同步,只需测得距离值即可定位,更易于实现,也是最常用的室内定位方法。利用现有设备,本文主要对基于距离交会原理的最小二乘算法和几何方法进行比较与分析,以寻求其中效率更高、收敛性更好、能够更为准确估计目标位置信息的算法。
1 距离交会定位在基于距离交会的定位方法中,假设存在3个基站Ai(xi, yi)(i=1, 2, 3),待测目标为Tag(x, y),其到各个基站的距离为Ri(i=1, 2, 3)。以基站Ai为圆心,距离Ri为半径,形成3个定位圆,即可唯一确定待测节点的位置。
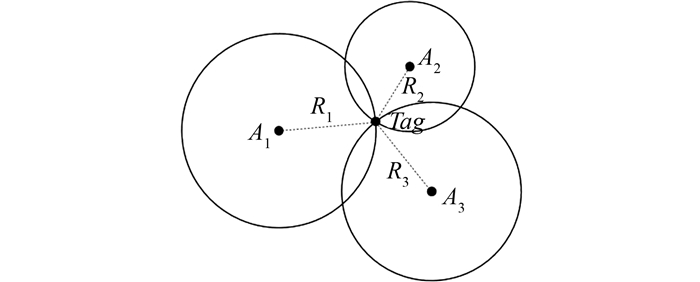 |
| 图 1 基于距离交会的定位原理 Fig.1 Positioning Principle Based on Range Rendeivous |
理想的距离交会定位中,几个定位圆必然交于一点,能够唯一确定目标的位置,但由于距离测量存在误差,将会交于一个小区域,使得待测节点位置信息与理想位置不同[10]。
1.1 最小二乘算法最小二乘(least squares, LS)算法是一种局部搜索算法[11]。若有N个基站,其坐标为Ai(xi, yi)(i=1, 2, …, N),到标签Tag(x, y)之间的距离为Ri,设其坐标之间存在函数关系:
| $ {\mathit{f}_i}\left( {\mathit{x}, \mathit{y}} \right) = \sqrt {{{\left( {{\mathit{x}_i} - \mathit{x}} \right)}^2} + {{\left( {{\mathit{y}_i} - \mathit{y}} \right)}^2}} $ | (1) |
选定初始点(x0, y0),对式(1)进行泰勒级数展开可得到式(2):
| $ {\mathit{f}_i}\left( {\mathit{x}, \mathit{y}} \right) = {\mathit{f}_i}\left( {{\mathit{x}_0}, {\mathit{y}_0}} \right) + \left( {\Delta x\frac{\partial }{{\partial x}} + \Delta y\frac{\partial }{{\partial y}}} \right){\mathit{f}_i}\left( {{\mathit{x}_0}, {\mathit{y}_0}} \right) $ | (2) |
将式(2)转换为矩阵形式有:
| $ \mathit{v} = \mathit{\boldsymbol{BX}} - \mathit{\boldsymbol{l}} $ | (3) |
式中,
通过加权最小二乘对式(3)求解得到式(4),P表示观测值的权阵:
| $ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{B}}^T}\mathit{\boldsymbol{PB}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{B}}^T}\mathit{\boldsymbol{Pl}}} \right) $ | (4) |
| $ \mathit{x} = {\mathit{x}_0} + \Delta x, \mathit{y} = {\mathit{y}_0} + \Delta \mathit{y} $ | (5) |
通过式(4)、式(5)改变初始值进行下一次计算,直到满足|Δx| < ε和|Δy| < ε时,结束迭代。
最小二乘算法是目前求解非线性方程有效的方法之一,当观测数据服从正态分布时,是所有估计中的最优估计,定位精度高;但其计算过程较为复杂,不具备抗差性,少量的粗差即可造成不可靠的参数估计,并且迭代次数和位置精度均受初始值的影响[12]。
1.2 几何方法假设存在4个基站Pi(xi, yi, zi)(i=1, 2, 3, 4),待测目标为T(x, y, z),待测节点到各个基站的距离为ri,则几何方法流程如图 2所示。其中几何精度因子(geometric dilution of precision, GDOP)是衡量定位精度的重要标准之一。
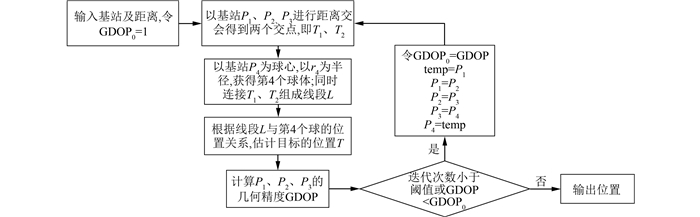 |
| 图 2 几何方法流程图 Fig.2 Flow Chart of Geometric Method |
由直线L与第4个定位圆的位置关系估计待测目标的最优解时需要进行如下判断。
记由3个基站估计得到的两个位置为T1、T2,联立L与第4个球可得一元二次方程:
| $ \mathit{a}{\mathit{\mu }^2} + \mathit{b\mu } + \mathit{c} = 0 $ | (6) |
其中,
μ的取值范围表示交点在直线上与T1、T2的相对位置关系。
由式(7)即可得到标签位置的最终估计结果。
| $ \overrightarrow T = {\overrightarrow T _1} + \mu \left( {{{\overrightarrow T }_2} - {{\overrightarrow T }_1}} \right) $ | (7) |
本文对所介绍的最小二乘算法以及几何方法进行了实验,并对两种算法做了性能比较。
2.1 实验设备测距阶段使用DWM1000模块,设4个基站Ai(i=0, 1, 2, 3),标签安置于导轨上,通过导轨开关控制标签沿直线段匀速运动。DWM1000是UWB无线通信模块,负责时间戳的标记和模块间的通信。其测距原理主要是基于双向飞行法(two way-time of flight,TW-TOF)[13, 14]。
如图 3所示,Tround为基站从发射请求信号到接收回应信号的时间,Treply为标签从接收请求信号到发射回应信号的时间,由此,信号在两个模块之间单向飞行路程可由式(8)得到:
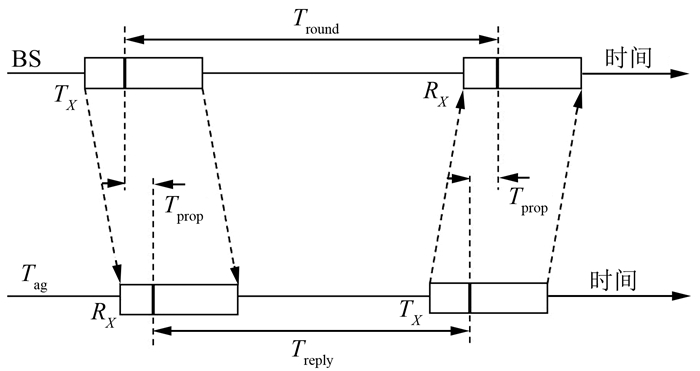 |
| 图 3 基于双向飞行法的测距原理 Fig.3 Ranging Principle of TW-TOF |
| $ {T_{{\rm{prop}}}} = \left( {{T_{{\rm{round}}}} - {T_{{\rm{reply}}}}} \right)/2 $ | (8) |
考虑场景为4 m×4 m的正方形区域,该区域中布置有已知位置坐标的基站以及一条导轨,导轨上架设待定位标签。在实验过程中,利用DWM1000模块获得的距离数据,分别采用LS算法和几何方法进行处理,比较最终定位结果。
在实验过程中,4个基站的位置不变,坐标分别为:A0(-1.2, 1.2, 0.9)、A1(-1.2, -1.8, 0.9)、A2(1.8,-1.8, 0.9)、A3(1.8,1.2, 0.9),在相同环境下进行了两组实验。
2.3 实验分析定位平面结果与LS定位平面结果如图 4、图 5所示。从图 4、图 5中数据可以看出,两种定位算法都能较为准确地估计标签的运动轨迹,但LS算法的定位结果收敛性优于几何方法结果;由表 1可知,与真实轨迹相比,LS算法定位偏差值小于0.02 cm,平均水平优于5 cm,胜过几何方法。
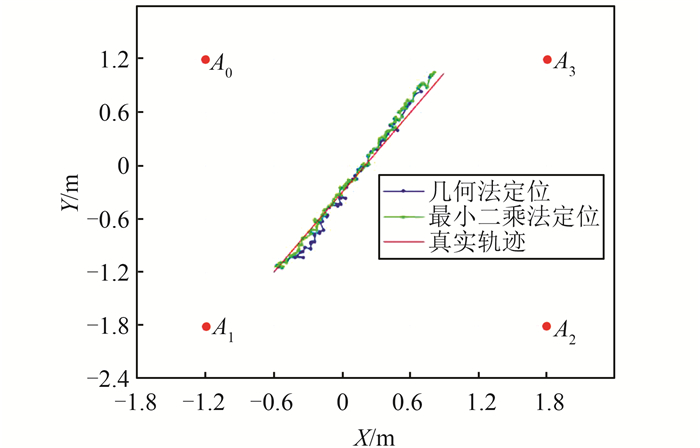 |
| 图 4 平面定位实验1结果 Fig.4 Result of Experiment 1 |
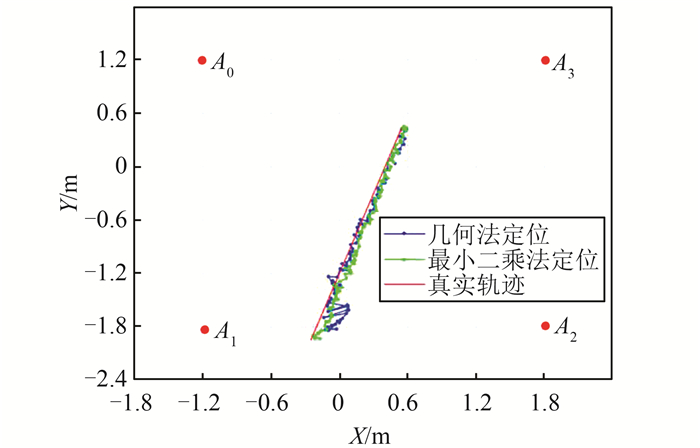 |
| 图 5 平面定位实验2结果 Fig.5 Result of Experiment 2 |
| 表 1 平面精度比较/m Tab.1 Comparison of Plane Accuracy/m |
 |
| 表 2 算法计算时间比较/s Tab.2 Comparison of Calculation Time of Algorithm/s |
 |
在两次实验中,对LS算法和几何定位算法的计算效率进行比较。计算两种算法定位所需时间,结果表明,几何定位算法运行时间约为LS算法的1/300,计算效率显著优于LS算法。对LS算法运行过程中的时间分配做了进一步分析发现,在使用LS算法对目标运动轨迹进行估计时,99.7%的时间均用于矩阵运算,而几何法只需进行简单的矢量运算。
3 结束语实验表明,与几何方法相比,LS算法可以更为准确地估计待测目标的位置,但计算时间更长。在实际生活中,定位目标的运动范围往往更大,为较好地确定其运动轨迹,需要的定位次数也将大大增加,在这种情况下,采用几何方法定位所节省的时间是很可观的。并且,从图 4和图 5可以看出,两种算法的轨迹并不平滑,这是由于测量值及定位算法本身存在误差,下一步可以考虑采用卡尔曼滤波对结果进行预测和修正,从而得到平滑轨迹;并且引入并行方法加速矩阵运算,在海量数据情况下提高LS算法的计算效率。
| [1] |
纪龙蛰, 单庆晓. GNSS全球卫星导航系统发展概况及最新进展[J]. 全球定位系统, 2012, 37(5): 56-61. |
| [2] |
朱庆, 熊庆, 赵君娇. 室内位置信息模型与智能位置服务[J]. 测绘地理信息, 2014, 39(5): 1-7. |
| [3] |
嵇茂祥. UWB室内定位系统研究与实现[D]. 上海: 华东师范大学, 2017: 9-10
|
| [4] |
邹进贵, 王涛, 龙凤阳. 一种改进的圆柱体定位算法研究与应用[J]. 测绘地理信息, 2014, 39(6): 7-9. |
| [5] |
Gezici S, Tian Z, Giannakis G B. Localization via ultra-wide-band radios: A Look at Positioning Aspects of Future Sensor Networks[J]. IEEE Signal Processing Magazine, 2005, 22(4): 70-84. DOI:10.1109/MSP.2005.1458289 |
| [6] |
Fang B T. Simple Solutions for Hyperbolic and Related Fixes[J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(5): 748-753. DOI:10.1109/7.102710 |
| [7] |
Chan Y T, Hang H Y C, Ching P C. Exact and Approximate Maximum Likelihood Localization Algorithms[J]. IEEE Transactions on Vehicular Technology, 2006, 55(1): 10-16. DOI:10.1109/TVT.2005.861162 |
| [8] |
吴君钦, 金巧, 吴云龙. 一种分布ML的VBLAST检测算法[J]. 信息技术, 2015(3): 17-24. |
| [9] |
高国伟, 白国振, 杨勇明. 基于RFID的改进室内三边定位算法研究[J]. 信息技术, 2017(5): 75-78. |
| [10] |
朱永龙. 基于UWB的室内定位算法研究与应用[D]. 山东: 山东大学, 2014: 7-15
|
| [11] |
Foy W H. Position-Location Solutions by Taylor-Series Estimation[J]. IEEE Transactions on Aerospace & Electronic Systems, 1976, AES-12(2): 187-194. |
| [12] |
吕志鹏, 隋立芬. 基于非线性高斯-赫尔默特模型的结构总体最小二乘法[J]. 武汉大学学报·信息科学版, 2019, 44(12): 1808-1815. |
| [13] |
牛群峰, 曹一帆, 王莉, 等. 基于TW-TOF的UWB室内定位技术与优化算法研究[J]. 自动化与仪表, 2018, 33(1): 5-9. |
| [14] |
王冰, 刘炎炎, 李清泉, 等. 基于传统超宽带的室内高精度动态定位算法[J]. 测绘地理信息, 2018, 43(4): 28-33. |
 2021, Vol. 46
2021, Vol. 46

