| 改进TERCOM算法用于重力场辅助惯性导航 |
重力辅助惯性导航系统(gravity-aided inertial navigation system, GAINS)被广泛用于载体航行中,以控制误差积累导致的位置发散。通过对比重力传感器测得的重力信息和重力基准图上获取的重力信息,可以更新载体的状态。
GAINS的匹配算法对于定位的精度和效率有巨大影响。依据算法的特点,可以将它们分为基于滤波的匹配算法和相关极值匹配算法两类。滤波匹配算法有桑迪亚惯性地形辅助导航(Sandia inertial terrain-aided navigation, SITAN)算法,即扩展卡尔曼滤波(extended Kalman filter, EKF)、无迹卡尔曼滤波(unscented Kalman filter, UKF)、并行卡尔曼滤波(parallel Kalman filter, PKF)、粒子滤波(particle filter, PF)等。相关极值匹配算法包括地形轮廓匹配算法(terrain contour matching, TERCOM)、最近等值线迭代算法(iterated closest contour point,ICCP)等[1, 2]。其中,TERCOM由于原理简单、可靠性高而被广泛应用。但其只是通过刚性变换来纠正位置误差,而实际应用中惯导在不同方向上具有不同的误差特性,以及同一方向误差受各种因素的影响也在不断的变化,这就决定了位置上的偏差不可能只用平移的方式进行消除[3, 4]。本文针对TERCOM算法存在的问题,提出了带有旋转和尺度变换功能的改进TERCOM算法。实验结果表明,改进型TERCOM算法比传统TERCOM算法优越。
1 改进TERCOM算法的原理传统TERCOM主要是选取一组和惯导指示航迹平行的序列,然后计算序列对应的重力异常值和重力异常观测值之间的相关性或者距离,依据一定的判定原则确定其中一条序列作为匹配结果序列[5, 6]。本文针对传统TERCOM算法存在的只能进行平移变换的问题,提出了带有旋转和尺度变换功能的改进TERCOM算法。其中,旋转的角度和尺度变换的具体操作依据惯导的误差状况进行确定。步骤如下:①通过平移变换获得平移搜索的一条航迹;②将终点在一个匹配序列所经历的时间段中积累的位置误差投影在与航行方向垂直的方向上,并适当处理获得旋转角度的范围, 然后按照一定的角度搜索间隔获得m个旋转角度;③将终点在一个匹配序列所经历的时间段中积累的位置误差投影在与航行方向平行的方向上获得尺度变换系数r,并将尺度变换系数按一定的间隔划分为n个;④利用旋转角度和尺度变换系数将l条平移得到的航迹进行旋转平移变换,得到l×m×n条轨迹;⑤进行匹配,并通过判别准则得到最佳位置。
图 1展示了旋转角度和尺度变换系数的确定方法。图 1中,P1为匹配序列的第一个点,Pn为匹配序列的最后一个点,
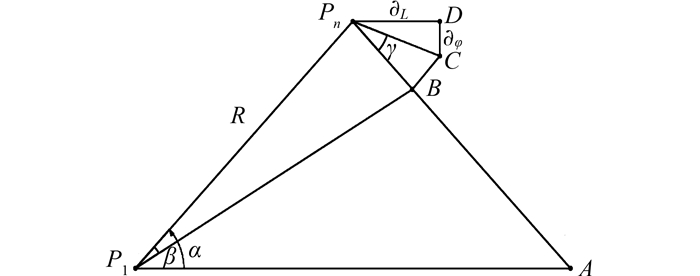 |
| 图 1 旋转与尺度变换参数确定 Figure 1 Determination of Rotation and Scale Transformation Parameters |
1) 旋转角度的确定。相关变量的计算公式为:
| $ \left\{ \begin{array}{l} \alpha {\rm{ = arctan}}\frac{{\sum\limits_{i = 1}^n {\Delta {\varphi _i}} }}{{\sum\limits_{i = 1}^n {\Delta {\lambda _i}} }}\\ \gamma = \frac{{\rm{ \mathsf{ π} }}}{2} - \alpha - {\rm{arctan}}\frac{{{\partial _\varphi }}}{{{\partial _L}}}\\ \beta = {\rm{arctan}}\frac{{\sqrt {\partial _\varphi ^2 + \partial _L^2} \cdot{\rm{cos}}\gamma }}{{\sqrt {{{\left( {\sum\limits_{i = 1}^n {\Delta {\varphi _i}} } \right)}^2} + {{\left( {\sum\limits_{i = 1}^n {\Delta {\lambda _i}} } \right)}^2}} }} \end{array} \right. $ | (1) |
式中,Δλi和Δφi分别为相邻两个航迹点在经度和纬度方向上的差距;α、γ是求解旋转角度时涉及的中间计算值。取正负两倍的β作为角度搜索范围,即为(-2β, +2β)。
2) 尺度变换系数r的确定。相关变量的计算方法为:
| $ r = {\rm{arctan}}\frac{{\sqrt {\partial _\varphi ^2 + \partial _L^2} \cdot{\rm{sin}}\gamma }}{{\sqrt {{{\left( {\sum\limits_{i = 1}^n {\Delta {\varphi _i}} } \right)}^2} + {{\left( {\sum\limits_{i = 1}^n {\Delta {\lambda _i}} } \right)}^2}} }} $ | (2) |
取尺度变换系数的两倍作为其搜索范围。需要注意的是,尺度变换系数通常很小,应当根据具体情况确定其搜索间隔,本文中按尺度变换系数大小的一半设定搜索间隔。
3) 待匹配航迹的旋转以及尺度变换。本文实验是在二维平面中进行的,因此,旋转与尺度的变换采用四参数变换法进行。
首先,求出匹配序列中其他航迹点相对于该次匹配的第一个点的坐标差,作为对应点的中间转换坐标(Δx′i, Δy′i),第一个点的坐标设为(0, 0);然后,对中间转换坐标进行转换,转换公式为:
| $ \left\{ \begin{array}{l} \Delta {x_i} = \Delta x{\prime _i}({m_j} + 1){\rm{cos}}{\mu _j} - \Delta y{\prime _i}({m_j} + 1){\rm{sin}}{\mu _j}\\ \Delta {y_i} = \Delta x{\prime _i}({m_j} + 1){\rm{sin}}{\mu _j} + \Delta y{\prime _i}({m_j} + 1){\rm{cos}}{\mu _j} \end{array} \right. $ | (3) |
式中,mj和μj分别为根据尺度变换系数的搜索间隔确定的第j次变换中的尺度变换系数和旋转角度。转换后的坐标(xi, yi)为:
| $ \left\{ \begin{array}{l} {x_i} = \Delta x{\prime _i} + x{\prime _i}\\ {y_i} = \Delta y{\prime _i} + y{\prime _i} \end{array} \right. $ | (4) |
式中,(x′i, y′i)为转换前航迹点的坐标,是经过平移得到的。依据本节中的变换方法将惯导指示轨迹平移后的轨迹依次经过变换得到l×m×n条轨迹(l、m、n分别为平移变换、旋转角度、尺度变换系数的个数)[7, 8]。
2 实验分析 2.1 实验数据重力背景图可以选取重力异常图或者重力梯度图,全球重力梯度图目前还没有公布[9],本文选取重力异常图作为背景图,如图 2所示。
 |
| 图 2 实验区域重力异常粗糙度图 Figure 2 Roughness Map of Gravity Anomaly of Experimental Area |
实验中用到的重力异常在圣地亚哥大学的网站上下载得到。选取的导航区域为:北纬25°~30°,东经130°~135°。经度方向的间隔是1′,纬度方向的间隔小于但接近1′,重力异常的单位为mGal。
2.2 实验条件本文在实验区域选择了4条轨迹进行实验,每条轨迹中航速为经度和纬度方向上各为12 n mile/h和10 n mile/h。每条匹配序列长度为15个点,采样间隔为10 min。由于惯导的误差在经度方向上有累积的特性,所以实验中惯导的线性误差在经度方向上为2 n mile/h,在纬度方向上为1/6 n mile/h,经度和纬度方向上的初始位置误差为5 n mile,真实轨迹经、纬度方向上的随机误差为0.06 n mile,惯导指示轨迹经、纬度方向上的随机误差为0.12 n mile,重力异常观测误差为1 mGal[10]。
2.3 实验结果图 3(a)为改进TERCOM算法的匹配结果,图 3(b)为传统TERCOM算法的匹配结果。轨迹所处区域重力场信息丰富程度不同,是为了验证在不同情况下的匹配效果。对比图 3(a)和图 3(b)可知, 改进TERCOM算法的匹配效果要比传统TERCOM算法的匹配效果好。前者匹配后轨迹与真实轨迹的距离差相对于后者要小。将4条轨迹中传统TERCOM算法匹配结果的距离差绝对值减去改进型TERCOM算法匹配结果的距离差绝对值,其比较如图 4所示。图 4中,差值基本都大于0,表明改进型TERCOM算法的匹配误差比传统TERCOM算法的匹配误差小。
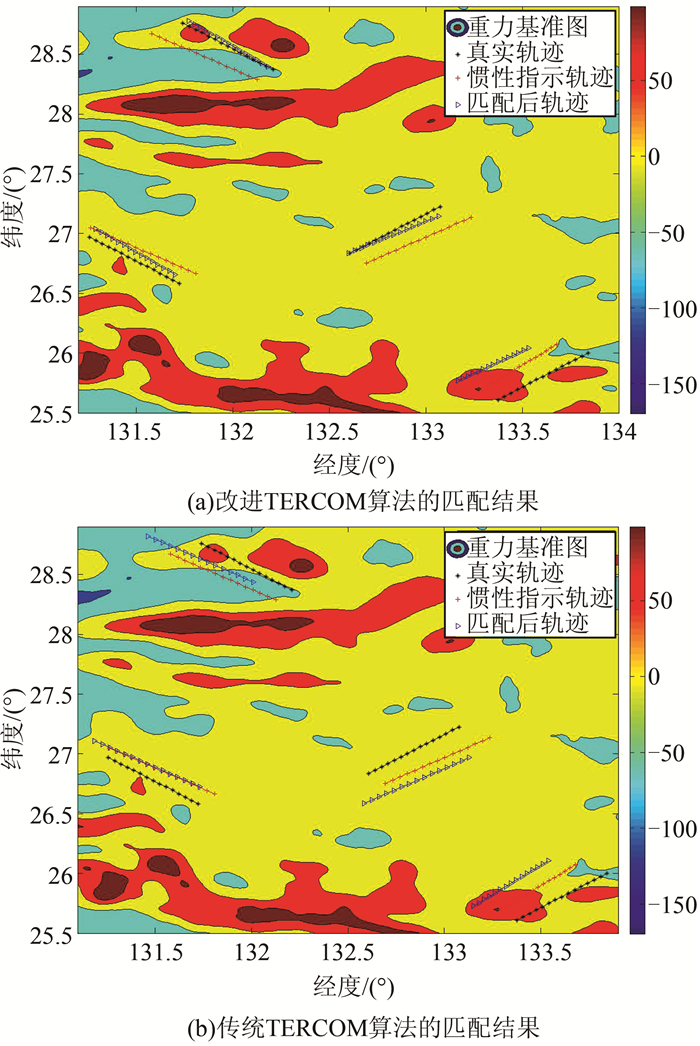 |
| 图 3 两种方法匹配效果 Figure 3 Matching Effects of Two Algorithm |
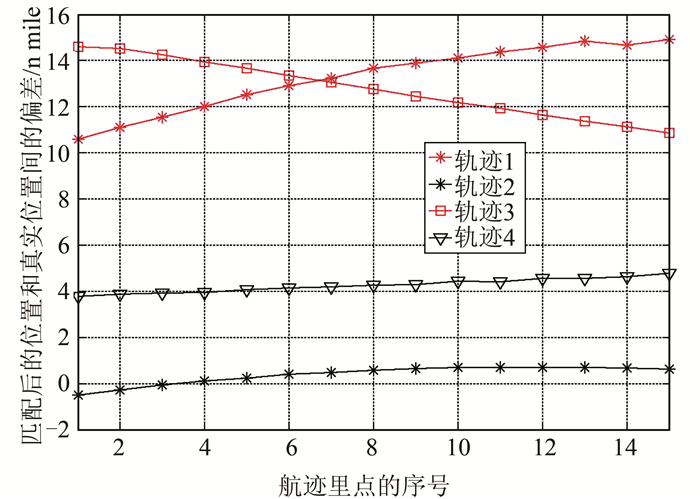 |
| 图 4 距离差绝对值比较 Figure 4 Comparison of Absolute Values of Distance Difference |
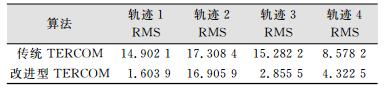
从表 1中可以看出,改进型TERCOM算法匹配结果的RMS都小于传统TERCOM算法。第1条、第3条和第4条轨迹中误差相差较大,第2条轨迹中两种算法的匹配结果都不理想,分析原因,是由于局部重力场特征的独特性不足导致的。因为TERCOM算法在搜索区域内对于匹配结果的选择只基于均方差算法(mean square difference, MSD)这一个指标,所以即使是在重力变化较显著的地区,只要搜索航迹上的特征接近于实际航迹,就可能出现误匹配的情况。总体上,实验结果表明了改进型TERCOM算法的优越性。
| 表 1 两种算法匹配结果统计/n mile Table 1 Statistics of Matching Results of Two Algorithms/n mile |
 |
3 结束语
本文针对传统TERCOM算法只能进行平移变换的问题提出了带有旋转和尺度变换功能的改进型TERCOM算法,较好地解决了由于惯导误差积累造成的指示位置中带有的旋转和尺度变换性质的问题。实验结果中,改进型TERCOM算法在相同的条件下匹配结果的精度要明显好于传统TERCOM算法,表明了改进型TERCOM的优越性和可行性。
| [1] |
张红伟. 水下重力场辅助导航定位关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013 |
| [2] | 赵建虎, 王胜平, 王爱学. 一种改进型TERCOM水下地磁匹配导航算法[J]. 武汉大学学报·信息科学版, 2009, 34(11): 1 320–1 323 |
| [3] | 李雄伟, 刘建业, 康国华. TERCOM地形高程辅助导航系统发展及应用研究[J]. 中国惯性技术学报, 2006, 14(1): 34–40 |
| [4] |
阮育铭, 张常云. 机动飞行的TERCOM算法[C]. 中国航空学会控制与应用学术年会, 烟台, 2004 |
| [5] | 闫利, 崔晨风, 吴华玲. 基于TERCOM算法的重力匹配[J]. 武汉大学学报·信息科学版, 2009, 34(3): 261–264 |
| [6] |
冯庆堂, 沈林成, 朱华勇, 等. 连续TERCOM相关匹配算法[C]. 全国空间及运动体控制技术学术会议, 长沙, 2002 |
| [7] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2009 |
| [8] | 胡国荣, 崔伟宏. 组合GPS/GLONASS在车辆导航和监控系统中的应用探讨[J]. 测绘工程, 2000, 9(4): 19–21 |
| [9] | 宁津生, 王正涛. 地球重力场研究现状与进展[J]. 测绘地理信息, 2013, 38(1): 1–7 |
| [10] |
李姗姗. 水下重力辅助惯性导航的理论与方法研究[D]. 郑州: 信息工程大学, 2010 |
 2017, Vol. 42
2017, Vol. 42

