| 多种点特征的影像匹配质量比较 |
2. 武汉大学遥感信息工程学院,湖北 武汉,430079
2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
影像匹配一直以来都是计算机自动化的研究重点。在数字摄影测量中,影像匹配可以用于得到同名点[1];在遥感科学中,遥感影像配准需要高精度的控制点[2];在计算机视觉[3]中,无论是人脸检测、运动检测以及模式识别,影像匹配都是理论基础。数字影像的基本单位是像素,其次是点特征、线特征、面特征以及对象[4]。点特征由于更接近影像的本质,因此是研究最多也是最成熟的一种特征。关于点特征的比较文献较多,Mikolajczyk等对几种常见的影像特征做了全面而细致的比较[5],包括仿射变换、尺度变化、影像旋转、影像模糊、JPEG压缩、明暗变化等;Luo等比较了SIFT (scale-invanriant feature transform)[6]、PCA-SIFT[7]以及SURF (speed-up robust features)[8]在模式识别中的表现[9],重点比较了这3种点特征的尺度、旋转、模糊、明暗变换以及仿射变换的特性;袁修孝等比较了几种常见的仿射不变算法在倾斜影像匹配中的效果,并给出了指导性的建议[10]。
对于全自动空中三角测量而言,影像匹配同样是必不可少的环节之一,然而航空影像与其他类型影像在几何和辐射上有较大差别,且对匹配结果的要求也与其他领域对匹配结果的要求不尽相同。在航摄飞行中往往按照一定的航摄规范进行,航摄相片往往具有较为规律的航向与旁向重叠度,且航摄比例尺也较为固定 (对于同一测区而言,构架航线与测图航线也只相差10%~15%),影像模糊等因素也可基本忽略不计。即使对于以无人机和无人飞艇为航摄平台的航摄影像而言,其航摄比例尺、太阳光照等都基本一致,变化较大的因素是影像旋偏角。因此对于航摄影像的匹配而言,点特征的尺度变化、模糊、明暗变化以及仿射变换都不是本文考虑的重点。此外,作为空中三角测量平差的观测值,影像匹配的精度是第一要求,同时算法的效率和稳定性也是空中三角测量自动影像匹配需首要考虑的因素。而影响匹配精度的因素主要包括匹配算子的特征定位精度和误匹配率;匹配的稳定性主要包括特征重复率和匹配点分布率。
鉴于此,本文给出了5种匹配质量评价指标,并使用其对3种常见的点特征匹配算子SIFT、SURF以及Harris[11]进行对比,以期评价其匹配质量,从而指导实际生产。
1 点特征匹配的基本理论摄影测量中较为常用的点特征匹配算子有SIFT特征匹配算子、SURF匹配算子、Harris匹配算子。限于篇幅,重点介绍与与本文提出的评价指标有关的理论。
1.1 Harris特征Harris角点是一类比较经典的角点类型,这类方法通过计算点的梯度和曲率来实现特征点的检测。对于某个待定点而言,若对于某个给定窗口,在其上的任意方向移动均能产生较大的灰度变化,则该待定点是一个Harris特征点。
对于影像中 (u, v) 处的像素而言,平移 (x, y) 形成的灰度变化可以表示为:
| $ \begin{array}{l} E(x,y) = \sum\limits_{u,v} {w(u,v){{[I(u + x,v + y) - I(u,v)]}^2}} \\ = \sum\limits_{u,v} {w(u,v){{[xX + yY + O({x^2},{y^2})]}^2}} \end{array} $ | (1) |
式中,I() 表示影像的灰度函数;O() 表示高阶无穷小;X、Y使用下面的公式计算:
| $ \begin{array}{l} X = I \otimes (-1, 0, 1) \approx \partial I/\partial x\\ Y = I \otimes {(-1, 0, 1)^T} \approx \partial I/\partial y \end{array} $ | (2) |
于是式 (1) 可以写为:
| $ E(x, y) = A{x^2} + B{y^2} + 2Cxy $ | (3) |
式中,A=X2⊗w, B=Y2⊗w, C=(XY)⊗w,w为高斯卷积窗口,用于消除影像噪声的影响。很明显,式 (3) 是一个二次型,与自相关函数有密切关系,且其描述了影像局部范围内灰度分布情况。式 (3) 可以写成下式:
| $ \mathit{\boldsymbol{E}} = (x, y)\left[{\begin{array}{*{20}{c}} A & C\\ C & B \end{array}} \right]{(x, y)^{\rm{T}}} = (x, y)\mathit{\boldsymbol{M}}{(x, y)^{\rm{T}}} $ | (4) |
M一般称为Harris矩阵,是判断当前点 (u, v) 的关键。当M具有两个大的正特征值时,任意地移动 (x, y) 计算得到的E较大,因此是一个角点;同理,当两个特征值都较小时,E较平滑,不能形成点特征;当有一大一小的特征值时,则在某一方向的平移引起的E较大,而其他方向较小,因此是一边缘。
在检测出来角点特征之后,还需要对角点特征进行精确定位,一般采用梯度拟合的方式进行,同时还需要对角点特征进行描述。对此,使用SIFT特征描述符对Harris特征进行描述
1.2 SIFT特征SIFT (尺度不变特征变换) 算法是一种优秀的点特征提取算子,在不同尺度空间求出不同尺度下的特征点,多个尺度拟合出特征点位置,并根据多层尺度空间描述特征点,使特征点具有尺度、旋转不变性质。
根据尺度空间理论,归一化的高斯拉普拉斯核是真正的尺度不变核函数,Lowe使用高斯差分影像近似表达高斯拉普拉斯影像,从而进一步提高了极值点探测效率。在检测点特征时,使用尺度空间影像的26邻域内的灰度极值点作为初始特征点。在点特征的精确定位时,将高斯差分影像进行泰勒展开:
| $D(x) = D + \frac{{\partial {D^{\rm{T}}}}}{{\partial x}}x + \frac{1}{2}{x^{\rm{T}}}\frac{{{\partial ^2}D}}{{\partial {x^2}}}x $ | (5) |
式中,D为高斯差分影像;x=(x, y, σ) 为当前点的偏移量,其中σ为当前点的尺度。为了得到当前点灰度的极值,令上式为0,可得:
| $ \hat x =-\frac{{{\partial ^2}{D^{-1}}}}{{\partial {x^2}}}\frac{{\partial D}}{{\partial x}} $ | (6) |
上式为取得灰度极值时当前点的偏移量。
将式 (6) 代入式 (5) 可得:
| $ D(\hat x) = D + \frac{1}{2}\frac{{\partial {D^{\rm{T}}}}}{{\partial x}}\hat x $ | (7) |
式 (7) 是当前点偏移x之后获取的最大灰度的极值。为了得到稳定的极值点,一般要求
为了提高特征稳定性和重复率,SIFT算子的另一个重要处理是剔除边缘点,使用Hessian矩阵:
| $\mathit{\boldsymbol{H}} = \left[{\begin{array}{*{20}{c}} {{D_{xx}}} & {{D_{xy}}}\\ {{D_{xy}}} & {{D_{yy}}} \end{array}} \right] $ | (8) |
式中,Dxy、Dxx、Dyy表示高斯差分影像在水平和垂直方向的二阶导以及混合二阶导。与Harris算子类似,当Hessian矩阵的最大特征值与次大特征值之比大于10时,认为是一个边缘点,是一个不稳定的特征点,应加以剔除。
在探测到SIFT特征之后,接下来需要对特征进行描述。SIFT采用128维的描述向量来描述SIFT特征。如图 1所示,图 1(a)、1(c)中的黑点表示当前特征点的位置,把其周围16×16个像素均等地划分为4×4个像素组成的正方形区域,统计每个小区域内的梯度,组成一个具有8个柱的梯度直方图,因此共有8×16=128个灰度梯度,即是一个128维的描述符。
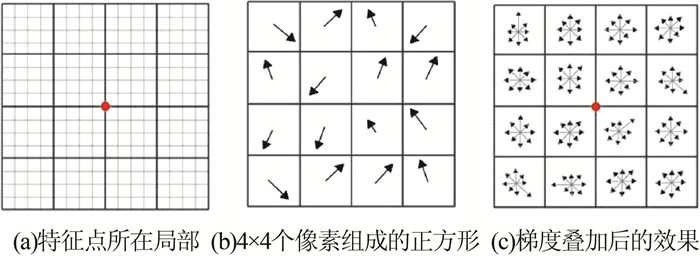 |
| 图 1 描述符生成示意图 Figure 1 Sketch of the Feature Descriptor |
1.3 SURF算子
SURF的特征提取算法是SIFT算法的加速。SURF在两个方面对SIFT进行了改进,首先使用盒式滤波器近似表达高斯差分影像,从而有利于发挥积分影像的效率优势,同时改进了SIFT特征描述符,将SIFT的128位描述符降低为64位。在特征点检测与特征点定位方面与SIFT基本没有区别。
2 评价指标及方法针对摄影测量中空中三角测量平差对匹配点的要求,本文提出5种评价点特征匹配质量的评价标准,即误匹配率、匹配点分布、特征重复率、匹配点精度以及匹配效率。
2.1 误匹配率误匹配率是影响匹配精度的一个重要因素。对于空中三角测量平差而言,当误匹配过高带来过量的粗差时,将严重影响相对定向的精度,继而影响空三加密的结果。因此误匹配率是本文评价影像匹配质量的一个重要指标。误匹配率的计算方法为错误匹配的点n与总匹配点数N之比:
| $ c = n/N $ | (9) |
为确保得到不包含粗差的匹配点,本文使用基于RANSAC[12]和基础矩阵[13]的粗差检测方法,同时通过人工检查,确保无匹配率的统计误差小于1%。
2.2 匹配点分布匹配点分布也是影响空中三角测量中相对定向的重要因素。从理论上讲,当匹配点均匀分布时,有利于提高空中三角测量的精度。本文采用基于Delaunay三角网的空间分布统计方法[14]:
| $ \left\{ \begin{array}{l} D = {D_A} \times {D_s} = \sqrt {\frac{{\sum\limits_i {(\frac{{{A_i}}}{{\bar A}}-1)} }}{{n-1}}} \times \sqrt {\frac{{\sum\limits_i {({S_i}-1)} }}{{n - 1}}} \\ \bar A = \frac{{\sum\limits_i {{A_i}} }}{n};{S_i} = \frac{{3\max ({J_i})}}{\pi } \end{array} \right. $ | (10) |
式中,n为Delaunay三角网的数目;Ai是第i个三角形的面积;max (Ji) 是第i个三角形中的最大角;是三角形的平均面积。匹配点的分布是一个无量纲的量,值域为[0, 1],且当D的值越大时,表示分布越良好。
2.3 特征重复率特征重复率反映出点特征的可匹配性,一般而言,特征重复率越高,匹配算法越稳定,匹配效果也越好。特征重复率与式 (9) 中的误匹配率并不一定相关。特征重复率的计算方法是用一定数量的正确匹配点计算出两张影像的单应矩阵H[13],同时还可以计算出两张影像间的基础矩阵F。设点p(xl, yl)、q(xr, yr) 是一对匹配点,则满足:
| $ \left( {\begin{array}{*{20}{c}} {{x_l}}\\ {{y_l}}\\ 1 \end{array}} \right) = w\left( {\begin{array}{*{20}{c}} {{x_r}}\\ {{y_r}}\\ 1 \end{array}} \right) + \Delta \mathit{\boldsymbol{l}} $ | (11) |
式中,w为常数;Δl为误差项。
同时,还应满足:
| $ d(p, l) < \sigma $ | (12) |
式中,d(q, l) 为q点到p核线的核线l的距离。在理想状况下,匹配点一定位于其对应核线上,在实际应用中,由于存在量测误差,σ为一个较小的值。同时,p、q的灰度的相关系数应该满足一定的条件:
| $ {\rm{Cov}}(p, q) > t $ | (13) |
因此,对于一个匹配点,应该同时满足式 (11)、式 (12) 及式 (13)。在本文的实验中,Δl=(20, 20, 1)T,σ=3,t=0.9。
2.4 匹配点精度在摄影测量中评价匹配精度的重要指标是相对定向[15],相对定向是用两张相互重叠的影像构成立体模型,是立体摄影测量的基础。立体像对的相对定向就是要恢复摄影时相邻两影像摄影光束的相互关系,从而使同名光线对对相交。相对定向的方法有两种:单独像对法和连续像对法。为了保证相对定向的精度,本文采用严格的粗差探测方法,即是对于所有的同名点而言,必须同时满足式 (11)、式 (12) 及式 (13)。
2.5 匹配效率对于点特征匹配而言,影响匹配效率的因素除了点特征匹配算子本身之外,还与匹配点数有关。SIFT、Harris以及SURF都采用KD-tree进行最近邻域搜索,当搜索的特征点样本数量很大时,势必影响搜索速度。因此,本文采用以下公式来计算匹配效率:
| $ s = T/N $ | (14) |
式中,T表示总的匹配时间;N表示整个测区内的匹配点数量;s的单位为 s/点对。
3 实验分析本文选择河南嵩山地区常规航空摄影影像作为实验数据,该测区采用UCD为航摄相机,摄影比例尺为1:8 000。嵩山测区地物类型较为丰富,地形以丘陵为主,包含山地、低矮丘陵以及大面积居民地,因此能很好地反映几种典型的点特征的匹配效果。本文选取其中的一条航带共计24张相片分别采用SIFT、Harris以及SURF算子进行匹配,并使用WUCAPS[16]进行相对定向结果作为匹配精度的评价。为了提高效率,将影像降采样到480×864,为了获取原始匹配精度,并不对初匹配点做精化处理 (例如最小二乘影像匹配[17])。图 2为使用本文指标的统计结果。
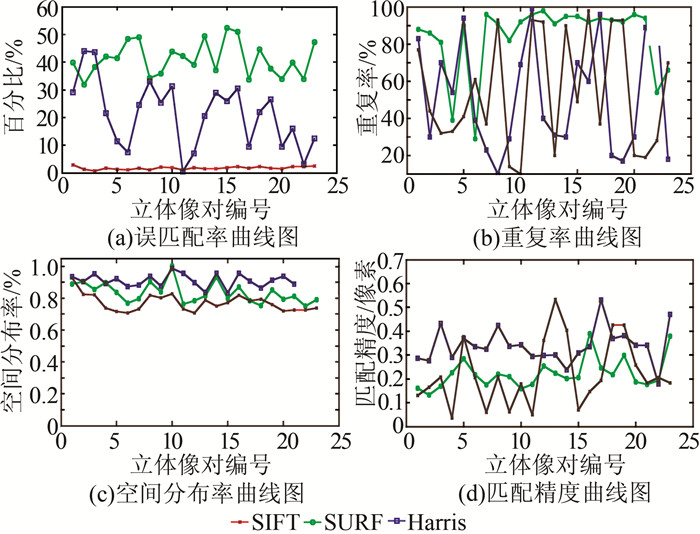 |
| 图 2 3种点特征的曲线图 Figure 2 Curves of Three Point Features |
图 2(a)是3种点特征的误匹配率曲线图。很明显,SIFT算子误匹配率最低,且误匹配率较稳定,都在2%左右。而基于SURF算子匹配点的误匹配率较高,在实验数据不理想的条件下,误匹配率超过50%。基于Harris匹配的结果误匹配率相对较少,但是该算法误匹配率与实验数据质量有关系,一般而言,误匹配率在20%左右,当数据质量较差时,误匹配率达40%,并且基于Harris算法的匹配稳定性不如SIFT和SURF。引起误匹配的主要原因是特征描述符的独特性引起的。如§1.2所述,SIFT描述符为一个128维向量,因此对每个点的描述更准确,不易形成误匹配;SURF描述符只要64维,相较SIFT描述符唯一性低,出现误匹配的概率变大;Harris特征在匹配时同样采用了SIFT的128维描述向量,但对于SIFT描述符而言,角点特征是不稳定的,在生成描述符时容易受噪声影响,出现描述错误,但总体说来,其误匹配率仍低于SURF的误匹配率。
图 2(b)是3种点特征的特征重复率曲线图。很明显,3种点特征的特征重复率无明显统计规律,都在0.1~1.0之间波动,特征重复率都不稳定。SURF提取的特征点重复率较高,且受数据质量影响不大,重复率基本都能保持在80%以上。而SIFT和Harris点特征对影像的纹理特征比较敏感。由式 (7) 可以得出,对于SIFT特征而言,只有当影像的局部灰度对比度超过阈值 (一般为0.03) 才会被认为是一个有效的特征点;同样对于Harris点特征,也要求特征值之比满足一定关系。因此,当影像的纹理丰富且影像的仿射畸变量较小时,特征重复率较高;反之,则特征重复率较低。需要注意的是,虽然SIFT的特征重复率较低,但是由于SIFT可以提取到丰富的特征点,仍然可以匹配到可观的匹配点。
图 2(c)是3种点特征的空间分布曲线图。可以看出,Harris特征匹配的空间分布最好,SURF次之,SIFT最差。3种点特征的空间分布基本一致,都在0.7~1.0之间,分布质量都较理想。
图 2(d)为3种点特征的匹配精度曲线图。可以看出,SIFT匹配精度最高,平均约为0.15个像素;SURF次之,约为0.2个像素,Harris相对较差,集中在0.3个像素。影像精度不稳定的原因有如下几点:
1) 特征算子本身的定位精度影响。由式 (6) 可知,SIFT算子定位是在高斯金字塔中,经过多层金字塔拟合得到。SURF虽然采用SIFT特征点定位策略,但是Hessian矩阵的卷积核不同,积分图像和滤波器的使用降低了定位精度,金字塔层数变化也影响特征点定位精度。Harris角点定位是通过初始角点与邻近点集梯度内积组成的矩阵计算得出,点位精度受邻近点数量、邻近点集灰度影响,定位精度不稳定,因此Harris匹配精度相对较差。
2) 匹配点的空间分布对匹配精度影响。当匹配点的空间分布较均匀时,匹配精度能与定位算子的精度基本保持一致;反之,则匹配精度低于定位算子本身的精度。
3) 误匹配率对匹配精度的影响。由误差处理理论可知,当平差系统中存在大量的粗差时,平差系统的精度受粗差影响严重,导致精度下降。因此系统粗差也是影响匹配精度的重要因素。
在本组实验中,由于点位分布基本一致 (图 2(c)),且本文采用了严格的粗差探测手段,因此此处的匹配精度大致地反映出了特征算子的定位精度。
此外,本文还选用了几组无人机影像作为实验数据,并使用本文提取的评价标准来评价SIFT、SURF以及Harris点特征匹配的匹配质量,其效果与嵩山测区的匹配效果基本一致,限于篇幅,这里不再赘述。
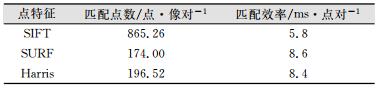
同时本文还对比了3种点特征的匹配效率。如表 1所示,可以看出,相对来讲,SIFT的匹配效率最高;SIFT和Harris的效率近似。然而,对于单个立体像对而言,由于SIFT得到的点数最多,因此SIFT的匹配效率又是最低的,而SURF和Harris近似相等。
| 表 1 3种点特征的匹配效率对比 Table 1 Matching Efficiency of Three Point Features |
 |
通过以上实验可以看出,在误匹配率方面,SIFT较SURF和Harris特征匹配好很多,在匹配精度方面,SIFT略优;在特征重复率和和空间分布方面,三者并无太大差别;而在匹配效率方面,虽然SIFT以像对为单位时匹配效率低,但却能得到大量的匹配点,具有较好的匹配稳定性。总的来说,SIFT点特征匹配是最适合作为空中三角测量影像量测中的匹配算法,较好地兼顾了效率、精度和稳定性。
4 结束语本文通过实验研究,给出了多种评价点特征匹配质量的标准,并通过一组实验分析了几种常用的点特征匹配算法的匹配效果。实验结果表明,SIFT特征匹配算子具有较低的误匹配率,较高的匹配精度,较好的匹配稳定性,是摄影测量影像 (无论是常规航摄影像还是无人机影像) 匹配的首选匹配算法。但SIFT匹配算法在时间效率上不是十分优秀,还需要使用其他的辅助手段进行运算加速,这也是今后进一步的研究内容。
| [1] | Gruen A. Development and Status of Image Matching in Photogrammetry[J]. The Photogrammetric Record, 2012, 26(137): 36–57 |
| [2] | 张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉: 武汉大学出版社, 2012 |
| [3] | Klette R. Concise Computer Vision[M]. London: Springer-Verlag, 2014 |
| [4] |
陈时雨. 基于PCA-SIFT的特殊纹理航摄影像匹配方法研究[D]. 武汉: 武汉大学, 2014 |
| [5] | Mikolajczyk K, Schmid C. A Performance Evaluation of Local Descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615–1630 DOI: 10.1109/TPAMI.2005.188 |
| [6] | Lowe D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110 DOI: 10.1023/B:VISI.0000029664.99615.94 |
| [7] | Yan K, Sukthankar R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington D C, USA, 2004 |
| [8] | Bay H, Tuytelaars T, Van Gool L. SURF: Speeded up Robust Features[M]. Berlin, Heidelberg: Springer, 2006 |
| [9] | Luo J, Gwun O, Luo J, et al. A Comparison of SIFT, PCA-SIFT and SURF[J]. International Journal of Image Processing, 2009, 3(4): 143–152 |
| [10] | 袁修孝, 陈时雨. 倾斜航摄影像匹配方法探究[J]. 测绘地理信息, 2015, 40(6): 1–6 |
| [11] | Harris C, Stephens M. A Combined Corner and Edge Detector[C]. The 4th Alvey Vision Conference, Alvey, UK, 1988 |
| [12] | Fischler M A, Bolles R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381–395 DOI: 10.1145/358669.358692 |
| [13] | Richard H, Andrew Z. Multiple View Geometry in Computer Vision[M]. London: Cambridge University Press, 2003 |
| [14] | Gonalves H, Gonalves J A, Corte-Real L. Measures for an Objective Evaluation of the Geometric Correction Process Quality[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(2): 292–296 DOI: 10.1109/LGRS.2008.2012441 |
| [15] | Yuan Xiuxiao. A Novel Method of Systematic Error Compensation for a Position and Orientation System[J]. Progress in Natural Science, 2008, 18(8): 953–963 DOI: 10.1016/j.pnsc.2008.02.005 |
| [16] | 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 2版. 武汉: 武汉大学出版社, 2012 |
| [17] | Ackermann F. Digital Image Correlation: Performance and Potential Application in Photogrammetry[J]. Photogrammetric Record, 1984, 11(64): 429–439 |
 2017, Vol. 42
2017, Vol. 42

