| 基于电离层经向分布特征的电离层拟合研究 |
2. 武汉大学测绘学院,湖北武汉,430079;
3. 山东省国土测绘院,山东济南,250013
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Shandong Institute of Land Surveying and Mapping, Ji'nan 250013, China
电离层在全球导航卫星系统(global navigation satellite system,GNSS)定位过程中作为主要误差源,极大限制了定位精度。GNSS信号传播过程中在电离层内部的折射和偏移是造成GNSS定位过程中电离层延迟的主要原因[1]。为了提高定位精度,要实时获取卫星和接收机间电离层穿刺点的电离层信息,一般用电离层总电子含量(total electron content,TEC)来描述电离层状态[2]。而目前观测技术不够成熟,观测设备数量稀少,无法实时获得任意位置的电离层情况。电离层应用过程中普遍使用如下方法实时获得与待处理位置相关联的TEC信息:①利用同一位置电离层穿刺点历史数据对现在时刻的TEC进行时间外推[3];②利用穿刺点周围固定参考站实时播发的TEC信息对当前位置的TEC进行实时内插[4]。常用的TEC内插方法有反距离加权法、克里金插值法和模型插值法等。反距离加权法将临近站点作为参考站,将参考站点和待插值站点间距离的倒数作为权值,计算加权平均数,得到待求点的值[5];克里金插值利用已有数据建立待插值点的最优线性无偏估计[6, 7];模型插值利用已有点拟合出残差最小的函数模型,将待求点代入模型后得到待求点插值结果,其可选模型包括简单多项式模型、三角函数模型和复杂的低阶球谐模型、球冠模型等[8, 9]。针对现有的反距离加权法受站间距影响较大、大范围插值效率低等问题[10],同时考虑到TEC在经向和纬向上的分布及变化规律[11],本文提出了一种新的基于电离层经向分布的多项式内插方法,以期在更低的站点密度下实现较高精度的插值效果。
1 电离层空间特征电离层内的分子和原子在太阳紫外线、Χ射线和高能粒子的作用下电离,产生自由电子和正、负离子。同时带电的氧离子和氮离子不断捕获自由电子,两个过程达到平衡最终构成了等离子体,等离子体中的电子密度已经足够影响GNSS卫星信号在电离层中的传播[12, 13]。太阳辐射是电离层的主要影响因素,地磁也会对电离层产生显著影响。太阳辐射在不同纬度的辐射量不同,不同季节太阳辐射的入射角不同,随着地球自转,一天中不同时刻的辐射量也不同[14]。由国际GNSS服务(International GNSS Service,IGS)组织发布的2014年年积日(day-of-year,DOY)75的UTC 0时、6时、12时、18时的全球电离层TEC等值线图可知,2014年DOY75的电离层活动在赤道电离层异常区域带(南北纬15°)最为活跃,电离层变化较为复杂。而在全球范围内,TEC在经向上基本呈现从赤道向两极递减的变化规律,而在纬向上基本均匀分布[11]。
2 基于经向TEC分布的多项式拟合方法针对同一经向上分布的观测站点,可建立沿经向分布的多项式拟合模型。由于直接采用测站天顶总延迟内插会引入投影误差[15]等,因此,实验数据均来自站点和卫星间的穿刺点斜路径总电子含量(slant TEC,STEC),防止引入不必要的误差源。此外,在进行内插拟合前,为了消除由接收机端和卫星端的硬件延迟引起的差分码偏差(differential code bias,DCB)[16],利用参与计算的基站及周围站点共同计算延迟量,并在计算过程中剔除该系统误差的影响。多项式拟合过程即为寻求一个到所有已知点的距离之和最小的非线性曲线的问题[17],根据穿刺点数量选择合适的阶数范围,列出待求解函数方程:
| $ \left[\begin{array}{c} S_1 \\ S_2 \\ \vdots \\ S_m \end{array}\right]=\left[\begin{array}{ccccc} 1 & x_1 & x_1{ }^2 & \cdots & x_1{ }^n \\ 1 & x_2 & x_2{ }^2 & & x_2{ }^n \\ \vdots & & & & \vdots \\ 1 & x_m & x_m{ }^2 & \cdots & x_m{ }^n \end{array}\right]\left[\begin{array}{c} a_0 \\ a_1 \\ \vdots \\ a_n \end{array}\right] $ | (1) |
式中,Si为某一时刻测站i与共视卫星连线的穿刺点的STEC观测值;xi为n阶多项式的输入变量,此处为测站点经度;ai为n阶多项式的参数。
通常采用最小二乘准则通过式(2)求解多项式拟合曲线的拟合参数:
| $ \boldsymbol{P}=\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{Y} $ | (2) |
式中,
同时,利用求解过程中产生的残差计算多项式模型的最优拟合阶数:
| $ {\rm{ Find }}{F_m}\mathop = \limits^{{\rm{def}}} \min \left[ {{\mathop{\rm std}\nolimits} \left( {\sum\limits_{t = 1}^k {{F_m}} \left( {{x_i}} \right) - {Y_i}} \right)} \right] $ | (3) |
式中,k为观测值个数;Fm为n阶多项式计算得到的结果;Yi为第i个STEC观测值。
利用预处理时计算得到无系统误差的穿刺点STEC值后,将同一时刻的穿刺点结果按照经度大小排序,由于测站位置固定,则每个时刻的穿刺点位置也将按照此相对位置排列。设定某个固定测站作为待求站后,利用除待求点外的其他点进行多项式拟合,再将待求点经度代入拟合函数,得到穿刺点STEC估计值,通过分析STEC估计值和解算值间的偏差程度,得到该方法的拟合效果。
3 实验及分析 3.1 数据选取与实验结果本文选取了位于太平洋和横贯美国的科罗拉多山脉之间的部分连续运行基准站(continuously operating reference station,CORS)系统站点进行分析。具体站点分布见图 1,相邻两个站点间距约100 km。将这一系列站的中间站点P127设定为待估点(验证点),使用除P127外的8个站的数据对P127站点数据进行TEC插值。
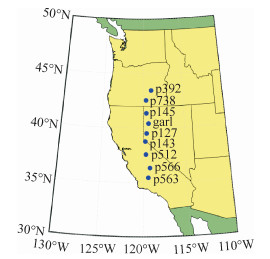 |
| 图 1 站点分布 Fig.1 Distribution of Sites |
对下载的数据进行预处理,分析每个站点数据的完整性和观测卫星数量。2014年3月第2周的观测数据完整性较好,同一颗卫星从升起至落下被所有站观测到的次数较多,可避免不同卫星对TEC观测结果造成的系统性偏差。同时,为了比较一天中不同时刻TEC估计的效果,本文以观测结果较好的2014年3月15日当地时间8时、14时和18时3个时间点前后各1 h的3个时段,统计每个时段内的共视卫星及各卫星的观测数据,如图 2所示。可以看出,在一天内,8时段、14时段可视卫星的观测数据量较为均衡,数据变化平稳,可用性较好。因此,本文实验数据为电离层较为平缓的8时段和电离层较活跃的14时段的观测数据。
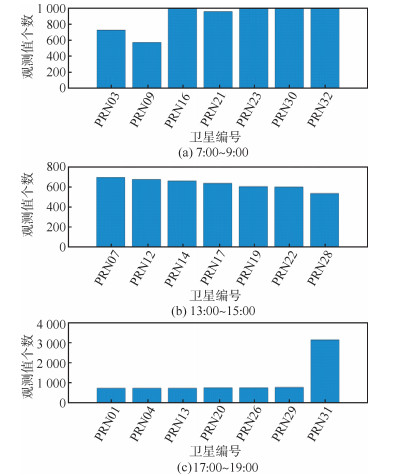 |
| 图 2 3个时段内的共视卫星及其观测数据(2014-03-15) Fig.2 Observation Data of the Common-View Satellites in Three Periods(2014-03-15) |
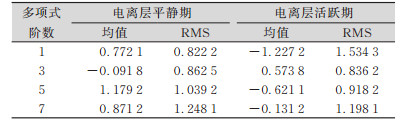
对2014年3月第2周的观测数据进行解算,得到所有共视卫星的穿刺点STEC。由于站点呈经向排列,得到的共视卫星在同一时刻的穿刺点也会呈经向排列,符合经向分布条件。利用各阶经向TEC多项式拟合方法拟合并内插后,比较7天内P127站各时段不同阶数多项式估计值与解算值的偏差的均值和均方根(root mean square,RMS),结果见表 1。电离层较平缓时,3阶多项式插值偏差的均值远低于其他阶次,RMS较低;电离层较活跃时,3阶多项式插值偏差的RMS最低,均值较低。综合而言,3阶多项式的内插精度优于其他阶次。P127站的内插结果与解算值的偏差见图 3。7天的插值偏差变化基本一致,随着观测数据增多,偏差不断减小,整体上其绝对值基本在2 TECU以内。
| 表 1 7天内各时段各阶多项式插值偏差/TECU Tab.1 Interpolation Bias for Polynomials in Various Orders in Each Period Within 7 Days/TECU |
 |
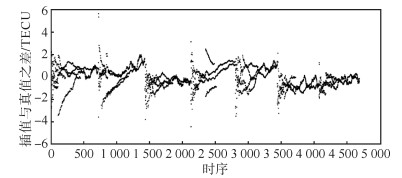 |
| 图 3 2014年3月第2周P127站3阶多项式的插值偏差 Fig.3 Interpolation Bias of 3rd Order Polynomial at P127 Station on the Second Week in March 2014 |
3.2 反距离加权法插值对比
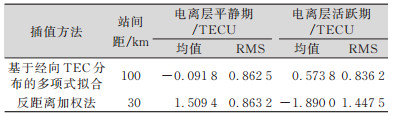
为了比较基于经向TEC分布的多项式内插法与反距离加权法拟合电离层的效果,在同一时间段内在P127站周围30 km处找了3个均匀分布的站点(P139、P128、P142)进行反距离加权内插。经过观测值文件预处理和共同求取DCB后,将利用这3个站的数据解算的穿刺点STEC进行反距离加权内插,并与基于经向TEC分布的多项式插值结果进行比较,结果见表 2。可以看出,无论在电离层较为平稳还是较为活跃时,基于经向TEC分布的多项式内插法插值偏差的均值和RMS均优于反距离加权法。
| 表 2 不同插值方法的插值偏差 Tab.2 Interpolation Bias of Different Interpolation Methods |
 |
3.3 站间距对拟合结果的影响
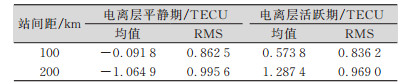
使用反距离加权等常规算法插值时,站间距是影响插值效果的一个重要因素。由于站点距离待求站越远,其空间相关性越低,插值效果下降。为了检验基于经向TEC分布的多项式拟合方法中站间距对拟合效果的影响,本文对进行插值的8个站进行抽稀,将站间距从100 km增加到200 km。抽稀后,利用剩余4个站对待插值站进行拟合,统一使用3阶多项式拟合并内插,得到站间距为200 km时,2014年3月第2周P127站的STEC内插值与解算值的偏差,见图 4。可以看出,STEC插值与解算值绝对偏差基本在3 TECU以内。为了进一步分析站间距对插值精度的影响,本文统计了不同站间距下电离层插值偏差的均值和RMS,见表 3。可以看出,抽稀后,站间距对插值偏差的RMS影响较小,但是站间距增加后,插值偏差的均值绝对值增大到1 TECU以上,表明站间距增加后,多项式拟合结果出现了系统性偏差。
 |
| 图 4 2014年3月第2周P127站站间距为200 km时的插值偏差 Fig.4 Interpolation Bias at P127 Station When the Spacing Is 200 km on the Second Week 2 in March 2014 |
| 表 3 不同站间距下插值偏差 Tab.3 Interpolation Bias Under Different Station Spacing Values |
 |
4 结束语
本文通过观察同经度上随纬度变化的一系列点,分析其TEC分布及变化规律,利用TEC在同经度下从高纬度到低纬度递减的空间分布特征,使用同经度分布的多个站进行多项式拟合并对待测点的STEC进行插值。结果表明,3阶多项式拟合能取得较优结果,且相较于常规反距离加权插值法,该方法在电离层平稳或活跃状态时拟合效果均较优,基本可以满足高精度定位过程中电离层误差改正需求;同时该方法站间距更大,能在更大范围内推广使用,在减少建站成本的情况下仍能保持电离层估计精度。
| [1] |
杨力. 大气对GPS测量影响的理论与研究[D]. 郑州: 信息工程大学, 2001
|
| [2] |
Hajj G A, Wilson B D, Wang C, et al. Data Assimilation of Ground GPS Total Electron Content into a Physics-Based Ionospheric Model by Use of the Kalman Filter[J]. Radio Science, 2004, 39(1): 1-17. DOI:10.3969/j.issn.1005-0388.2004.01.001 |
| [3] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报·信息科学版, 2011, 36(3): 267-270. |
| [4] |
Deviren M N, Arikan F, Arikan O. Spatio-Temporal Interpolation of Total Electron Content Using a GPS Network[J]. Radio Science, 2013, 48(3): 302-309. DOI:10.1002/rds.20036 |
| [5] |
薛树强, 杨元喜. 广义反距离加权空间推估法[J]. 武汉大学学报·信息科学版, 2013, 38(12): 1435-1439. |
| [6] |
朱永兴, 谭述森, 杜兰, 等. 顾及粗差影响的全球电离层克里金插值及精度分析[J]. 测绘学报, 2019, 48(7): 840-848. |
| [7] |
Orús R, Hernández-Pajares M, Juan J M, et al. Improvement of Global Ionospheric VTEC Maps by Using Kriging Interpolation Technique[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2005, 67(16): 1598-1609. DOI:10.1016/j.jastp.2005.07.017 |
| [8] |
Cui J H, Tang W M, Jin L, et al. An Improved Ionosphere Interpolation Algorithm for Network RTK in Low-Latitude Regions[J]. GPS Solutions, 2018, 22(4): 109. DOI:10.1007/s10291-018-0778-y |
| [9] |
柳景斌, 王泽民, 王海军, 等. 利用球冠谐分析方法和GPS数据建立中国区域电离层TEC模型[J]. 武汉大学学报·信息科学版, 2008, 33(8): 792-795. DOI:10.13203/j.whugis2008.08.006 |
| [10] |
Chen F W, Liu C W. Estimation of the Spatial Rainfall Distribution Using Inverse Distance Weighting(IDW) in the Middle of Taiwan[J]. Paddy and Water Environment, 2012, 10(3): 209-222. DOI:10.1007/s10333-012-0319-1 |
| [11] |
朱永兴, 谭述森, 明锋, 等. 顾及经纬度方向异性的电离层TEC IDW插值及精度分析[J]. 武汉大学学报·信息科学版, 2019, 44(11): 1605-1612. |
| [12] |
袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 北京: 中国科学院研究生院(测量与地球物理研究所), 2002
|
| [13] |
耿长江. 利用地基GNSS数据实时监测电离层延迟理论与方法研究[D]. 武汉: 武汉大学, 2011
|
| [14] |
蔡昌盛, 高井祥, 李征航. 利用GPS监测电离层总电子含量的季节性变化[J]. 武汉大学学报·信息科学版, 2006, 31(5): 451-453. |
| [15] |
刘利, 韩春好. 常见电离层延迟模型投影函数的分析比较[J]. 全球定位系统, 2001, 26(1): 43-45. DOI:10.3969/j.issn.1008-9268.2001.01.010 |
| [16] |
章红平, 施闯, 唐卫明. 地基GPS区域电离层多项式模型与硬件延迟统一解算分析[J]. 武汉大学学报·信息科学版, 2008, 33(8): 805-809. DOI:10.13203/j.whugis2008.08.007 |
| [17] |
陈永贵. 中国区域电离层建模及其精度分析[J]. 导航定位学报, 2021, 9(2): 104-108. |
 2022, Vol. 47
2022, Vol. 47


