| 多变量灰色马尔科夫模型在建筑物沉降预测中的应用 |
2. 北斗导航应用技术协同创新中心,河南 郑州,450052
2. Collaborative Innovation Center of BDS Research Application, Zhengzhou 450052, China
变形灾害的监测与预测研究是重大的安全问题之一。通过对已有变形监测数据的处理和分析研究,构建合理的预测模型,对变形体的安全监测与灾害预报工作具有极其重要的实际意义。灰色理论为预测模型的建立提供了有效的理论支持,其在建筑物的沉降监测预测中具有潜在的优势。近几年来,国内外学者围绕灰色理论在沉降监测预测方面的应用进行了大量研究。文献[1]将灰色理论与神经网络算法相结合,进行了矿区滑坡沉降监测预测分析,该方法可以获得较高精度的矿区滑坡沉降预测结果。文献[2]应用3种不同的灰色GM(1, 1)模型预测高速铁路隧道围岩沉降,在短期的预测中灰色GM(1, 1)模型能够满足隧道围岩沉降监测的需求。文献[3-6]利用初值的选取、背景值重构以及残差修正等,进行了传统灰色GM(1, 1)模型的优化研究。但传统的灰色GM(1, 1)模型没有充分考虑处于同一沉降体上各沉降点间的相关信息,不足以反映整个建筑物的沉降规律。同时考虑到处于同一沉降体的各个离散沉降监测点,建立多变量灰色MGM(1, n)模型[7]将会产生更好的预测效果。文献[8, 9]将优化的灰色MGM(1, n)模型分别应用到路基沉降和滑坡监测工程中,得到了比传统模型更好的预测结果。但对于沉降监测实测数据波动性大的问题,传统灰色及其优化模型都不能很好地解决。马尔科夫理论可有效地修正预测模型的残差,以弥补建模数据波动性给模型带来的局限性。文献[10-16]将灰色理论和马尔科夫理论相结合,构建了灰色马尔科夫模型,提高了预测模型的预测精度,改善了模型的稳定性。本文将多变量灰色MGM(1, n)模型与马尔科夫理论结合起来,建立多变量灰色马尔科夫模型,并应用于某高层建筑物沉降监测中,进行预测验证,并与传统模型进行比较分析。
1 多变量灰色马尔科夫模型 1.1 灰色MGM(1, n)模型多变量灰色MGM(1, n)模型能够较好地反映系统中各变量之间相互制约、相互影响的关系,且当n=1时,模型就退化为灰色GM(1, 1)模型。参考文献[7-9],其建模步骤如下:假设沉降体上有n个相关联的沉降观测点,实测n个观测点的m周期的沉降观测数据,其相应的沉降观测数据序列,记为{Xi(0)}。
| $ \begin{array}{*{20}{c}} {X_i^{\left( 0 \right)}\left( k \right) = \left[ {X_i^{\left( 0 \right)}\left( 1 \right),X_i^{\left( 0 \right)}\left( 2 \right), \cdots ,X_i^{\left( 0 \right)}\left( m \right)} \right],}\\ {k = 1,2, \cdots ,m;i = 1,2, \cdots ,n} \end{array} $ | (1) |
对数据{Xi(0)}序列进行一次累加,生成累加数据序列,记为{Xi(1)}。
| $ X_i^{\left( 1 \right)}\left( k \right) = \left[ {X_i^{\left( 1 \right)}\left( 1 \right),X_i^{\left( 1 \right)}\left( 2 \right), \cdots ,X_i^{\left( 1 \right)}\left( m \right)} \right] $ | (2) |
式中,
灰色MGM(1, n)模型的白化微分方程组形式为:
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}X_1^{\left( 1 \right)}}}{{{\rm{d}}t}} = {a_{11}}X_1^{\left( 1 \right)} + {a_{12}}X_2^{\left( 1 \right)} + \cdots + {a_{1n}}X_n^{\left( 1 \right)} + {b_1}\\ \frac{{{\rm{d}}X_2^{\left( 1 \right)}}}{{{\rm{d}}t}} = {a_{21}}X_1^{\left( 1 \right)} + {a_{22}}X_2^{\left( 1 \right)} + \cdots + {a_{2n}}X_n^{\left( 1 \right)} + {b_2}\\ \vdots \\ \frac{{{\rm{d}}X_n^{\left( 1 \right)}}}{{{\rm{d}}t}} = {a_{n1}}X_1^{\left( 1 \right)} + {a_{n2}}X_2^{\left( 1 \right)} + \cdots + {a_{nn}}X_n^{\left( 1 \right)} + {b_n} \end{array} \right. $ | (3) |
写成矩阵形式为:
| $ \frac{{{\rm{d}}{X^{\left( 1 \right)}}}}{{{\rm{d}}t}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{X}}^{\left( 1 \right)}} + \mathit{\boldsymbol{B}} $ | (4) |
式中,
离散化式(4),即可得到式(4)的灰色微分方程[8, 9]为:
| $ X_i^{\left( 0 \right)}\left( k \right) = \sum\limits_{j = 1}^n {{a_{ij}}Z_i^{\left( 1 \right)}\left( k \right)} + {b_i} $ | (5) |
式中,
式(3)的时间响应方程式(预测方程)为:
| $ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }^{\left( 1 \right)}}\left( t \right) = {{\rm{e}}^{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} \left( {t - 1} \right)}} \times \left[ {{X^{\left( 1 \right)}}\left( 1 \right) + {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} }}}^{ - 1}}\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} }}} \right] - {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} }}}^{ - 1}}\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} }} $ | (6) |
式中,
最后,恢复时间序列,还原得到预测值为:
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} _i^{\left( 0 \right)}\left( {k + 1} \right) = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} _i^{\left( 1 \right)}\left( {k + 1} \right) - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} _i^{\left( 1 \right)}\left( k \right) $ | (7) |
马尔科夫理论可以有效地处理沉降监测实测数据波动性大的问题,可弥补建模数据波动性给预测模型带来的局限性。将上述多变量灰色MGM(1, n)模型与马尔科夫理论相结合,建立多变量灰色马尔科夫预测模型,参考文献[10-12],其建模步骤如下:
1) 假设通过灰色MGM(1, n)模型得到的预测数据序列为
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} _i^{\left( 0 \right)}\left( k \right) = \left[ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} _i^{\left( 0 \right)}\left( 1 \right),\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} _i^{\left( 0 \right)}\left( 2 \right), \cdots ,\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} _i^{\left( 0 \right)}\left( m \right)} \right] $ | (8) |
2) 依据预测数据序列划分s个马尔科夫状态,参考文献[12],其状态区间记为:
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} _i^{\left( 0 \right)}\left( k \right) \in {E_i} = \left[ {{a_{1i}},{a_{2i}}} \right],i = 1,2,3, \cdots ,s $ | (9) |
式中,a1i、a2i分别表示为状态Ei的上下界。因此,总的状态集合E=(E1, E2, …, En)。为了使预测值充分利用近期的相关数据,减小随机误差的影响,构建n步状态转移概率元素Pij(n),并由n步转移概率元素构建n步转移概率矩阵P(n),其形式记为:
| $ {\mathit{\boldsymbol{P}}^{\left( n \right)}} = \left[ {\begin{array}{*{20}{c}} {p_{11}^{\left( n \right)}}&{p_{12}^{\left( n \right)}}& \cdots &{p_{1s}^{\left( n \right)}}\\ {p_{21}^{\left( n \right)}}&{p_{22}^{\left( n \right)}}&{}&{p_{2s}^{\left( n \right)}}\\ \vdots &{}&{}& \vdots \\ {p_{s1}^{\left( n \right)}}&{p_{s1}^{\left( n \right)}}& \cdots &{p_{ss}^{\left( n \right)}} \end{array}} \right],i = 1,2,3, \cdots ,s $ | (10) |
式中,
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {p_{i1}^{\left( 1 \right)}}&{p_{i2}^{\left( 1 \right)}}& \cdots &{p_{is}^{\left( 1 \right)}}\\ {p_{i1}^{\left( 2 \right)}}&{p_{i2}^{\left( 2 \right)}}&{}&{p_{is}^{\left( 2 \right)}}\\ \vdots &{}&{}& \vdots \\ {p_{i1}^{\left( s \right)}}&{p_{i2}^{\left( s \right)}}& \cdots &{p_{is}^{\left( s \right)}} \end{array}} \right] $ | (11) |
3) 取
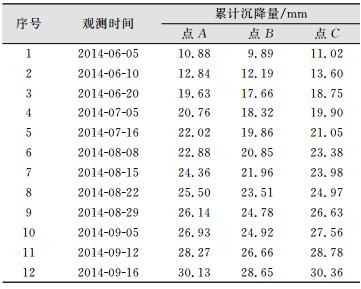
本文研究对象为银川市某项目新建的居民楼,在9#~16#栋居民楼布设28个沉降观测点,按照二等水准测量的要求进行往返测量,每次施测时对监测点进行累计沉降记录,以确定每栋楼沉降的稳定性。选取位于15#楼的A、B、C3个监测点的12期累计沉降量数据作为本次实验数据,其中前8期数据用于建模,后4期数据用于检验和比较预测值的准确性,原始的观测数据如表 1所示。
| 表 1 监测点原始数据序列 Tab.1 Original Data Sequence of Monitoring Points |
 |
2.1 多变量灰色马尔科夫模型的数据计算
选取表 1中A、B、C 3个监测点的前8期数据,以Matlab7.0软件为平台,按照§1.1的建模过程,并构建灰色MGM(1, 3)模型,同时计算3个监测点的前8期拟合值和后4期的预测值。在得出灰色MGM(1, 3)模型拟合值和预测值的基础上,利用马尔科夫理论分别对3个监测点的模型结果进行修正,得出最终的多变量灰色马尔科夫模型的预测结果。以监测点A前8期的MGM(1, 3)模型的拟合数据,进行马尔科夫修正过程,以及计算本文新模型第9期的预测值为例。其计算过程如下。
1) 经过MGM(1, 3)模型进行计算,监测点A的MGM(1, 3)模型的前8期拟合值,如表 2所示。
| 表 2 A点MGM(1, 3)的计算结果表/mm Tab.2 Results Table of A Point by MGM(1, 3) Model/mm |
 |
同时得到A点MGM(1, 3)模型的第9期预测值
2) 为计算方便,将表 2中的拟合数据序列划分为4种马尔科夫状态,划分标准如表 3所示[12-16]。
| 表 3 状态划分标准 Tab.3 Standard of Status Division |
 |
3) 按照式(10),计算4步转移概率矩阵:
| $ {\mathit{\boldsymbol{P}}^{\left( 1 \right)}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} 0\\ 0.3333\\ 0\\ 0 \end{array}&\begin{array}{l} 0\\ 0.3333\\ 0.5\\ 0 \end{array}&\begin{array}{l} 0\\ 0.3333\\ 0.5\\ 1 \end{array}&\begin{array}{l} 1\\ 0\\ 0\\ 0 \end{array} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{P}}^{\left( 2 \right)}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} 0\\ 0.1111\\ 0.1667\\ 0 \end{array}&\begin{array}{l} 0\\ 0.2778\\ 0.4167\\ 0.5 \end{array}&\begin{array}{l} 1\\ 0.2778\\ 0.4167\\ 0.5 \end{array}&\begin{array}{l} 0\\ 0.3333\\ 0\\ 0 \end{array} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{P}}^{\left( 3 \right)}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} 0\\ 0.0926\\ 0.1389\\ 0.1667 \end{array}&\begin{array}{l} 0.5\\ 0.5648\\ 0.3472\\ 0.4167 \end{array}&\begin{array}{l} 0.5\\ 0.2315\\ 0.3472\\ 0.4167 \end{array}&\begin{array}{l} 0\\ 0.1111\\ 0.1667\\ 0 \end{array} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{P}}^{\left( 4 \right)}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} 0.1667\\ 0.0772\\ 0.1157\\ 0.1389 \end{array}&\begin{array}{l} 0.4167\\ 0.3596\\ 0.2894\\ 0.3472 \end{array}&\begin{array}{l} 0.4167\\ 0.4707\\ 0.4560\\ 0.3472 \end{array}&\begin{array}{l} 0\\ 0.0926\\ 0.1389\\ 0.1667 \end{array} \end{array}} \right] $ |
4) 计算MGM(1, 3)模型的第9期预测值所处的马尔科夫状态。
在转移概率矩阵中挑选初始状态所对应的行向量组成概率转移矩阵,对对应的新矩阵列向量求和,其中的最大值,则是第9期预测值所对应的状态,如表 4所示。
| 表 4 第9期数据状态预测 Tab.4 Data's State Prediction Table of N0.9 |
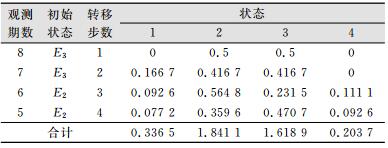 |
从表 4中的合计结果可以看出,最大值对应的状态为状态2。因此,MGM(1, 3)模型的第9期预测值所处的马尔科夫为状态E2。
5) 计算多变量灰色马尔科夫模型的第9期预测值。
从步骤4)可得出MGM(1, 3)模型的第9期预测值所处的马尔科夫状态为E2,参照表 3划分的马尔科夫状态表,MGM(1, 3)模型的第9期预测值所处的修正区间为
按照马尔科夫修正过程,分别建立A、B、C 3个监测点的多变量灰色马尔科夫模型, 利用郭兰兰等[6]提出的基于残差修正的模型建立灰色GM(1, 1)模型;按照§1.1中阐述的理论建立多变量灰色MGM(1, 3)模型。以Matlab7.0软件为平台,编写计算方式的相关程序,并计算3个监测点的第9~12期的预测值。A、B、C 3个监测点的3种模型预测结果如表 5所示。3种模型的数据与实测数据曲线比较图如图 1所示。
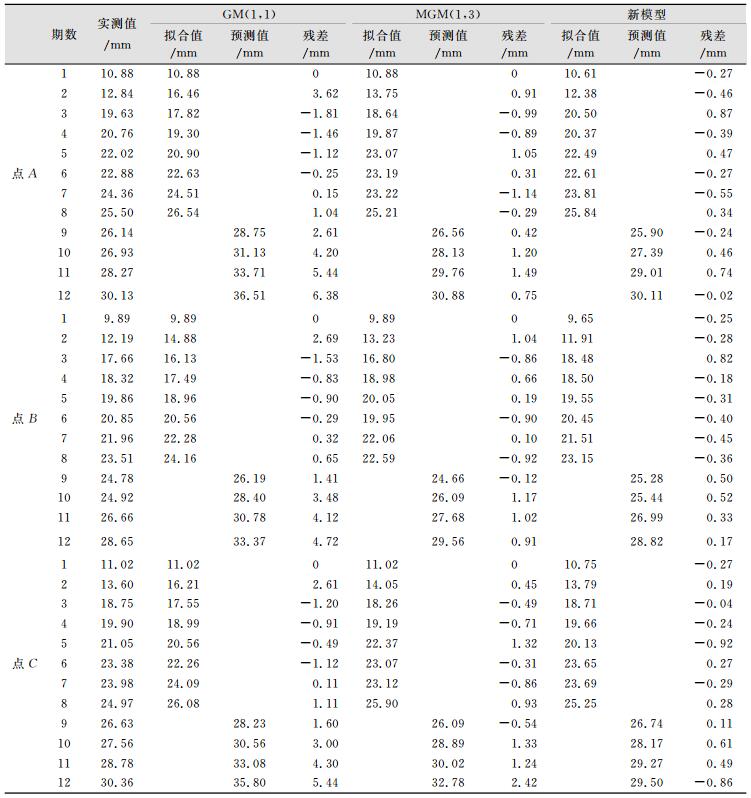
| 表 5 点A、B、C 3种模型拟合值和预测值 Tab.5 Fitted and Predictive Values of Three Models for the Point A、B、C |
 |
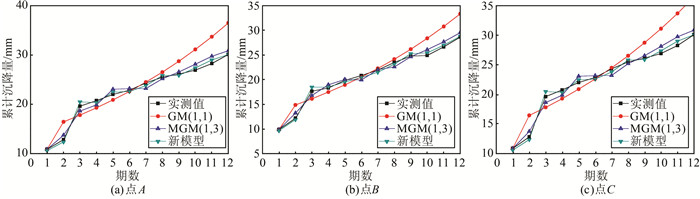 |
| 图 1 点A、B、C 3种模型的预测值与实测值比较图 Fig.1 Comparison Between Actual Measurements and Prediction Cures of Three Models of the Point A、B、C |
从表 5中可以看出,点A的多变量灰色马尔科夫模型的预测值残差中误差0.52 mm小于灰色GM(1, 1)模型的预测值残差中误差5.61 mm以及灰色MGM(1, 3)模型的预测值残差中误差1.21 mm;点B的多变量灰色马尔科夫模型的预测值残差中误差0.47 mm小于灰色GM(1, 1)模型的预测值残差中误差4.22 mm以及灰色MGM(1, 3)模型的预测值残差中误差1.04 mm;点C的多变量灰色马尔科夫模型的预测值残差中误差0.67 mm小于灰色GM(1, 1)模型的预测值残差中误差4.46 mm以及灰色MGM(1, 3)模型的预测值残差中误差1.78 mm。同时,从图 1中可以看出,3个监测点的多变量灰色马尔科夫模型的数据与实测值曲线拟合效果最好。从3个监测点的预测值可以看出,多变量灰色马尔科夫模型的预测值更具参考价值。
3 结束语本文针对传统的灰色GM(1, 1)模型只能进行单个建筑物沉降点的数据预测的问题,考虑到处于同一建筑物的各个离散沉降监测点具有相同的沉降特征和相关的动态沉降过程,使用灰色MGM(1, n)模型更加有效。同时,由于利用马尔科夫理论可以修正预测数据的扰动性,本文将灰色MGM(1, n)模型与马尔科夫理论耦合起来,建立了多变量灰色马尔科夫模型,并应用于某建筑物的沉降监测中,进行了预测验证与比较分析。结果表明,多变量灰色马尔科夫模型的预测稳定性和精度都要优于灰色GM(1, 1)和MGM(1, n)模型的结果,有效地克服了以往预测模型中信息不关联和因素扰动性大的缺陷。本文建立的多变量灰色马尔科夫模型,考虑到构建马尔科夫状态的方便,建议建模数据不要低于6期。同时应根据实测数据,及时更新建模数据,用最新的、更可靠的数据建立预测模型。
| [1] |
Cao Wangcheng, Liu Zhiyu, Zheng Lin. Application of Gray Neural Network in the Prediction of Slope Settlement[J]. International Journal of Applied Mathematics and Statistics, 2013, 51(22): 196-204. |
| [2] |
Guo Youlin, Zhao Minghua, Deng Zongwei. Tunnel Surrounding Rock Deformation Forecast Analysis Based on GM and FEM[J]. Electronic Journal of Geotechnical Engineering, 2014, 19: 1379-1394. |
| [3] |
张彬, 西桂权. 基于背景值和边值修正的GM(1, 1)模型优化[J]. 系统工程理论与实践, 2013, 33(3): 682-688. DOI:10.12011/1000-6788(2013)3-682 |
| [4] |
Wang Y H, Dang Y G, Liu S F. An Approach to Increase Prediction Precision of GM(1, 1) Model Based on Optimization of the Initial Condition[J]. Expert Systems with Applications, 2010, 37(8): 5640-5644. DOI:10.1016/j.eswa.2010.02.048 |
| [5] |
袁德宝, 崔希民, 高宁. 同时利用x(1)(1)和x(1)(n)为GM(1, 1)建模初始条件的预测方法研究[J]. 大地测量与地球动力学, 2013, 33(3): 79-82. |
| [6] |
郭兰兰, 邹志红, 安岩. 基于残差修正的GM(1, 1)模型在水质预测中的应用[J]. 数学的实践与认识, 2014, 44(19): 176-181. |
| [7] |
崔立志, 刘思峰, 吴正朋. 基于向量连分式理论的MGM(1, n)模型[J]. 系统工程, 2008, 26(10): 47-51. |
| [8] |
李世贵, 易庆林, 吴娟娟, 等. 背景值优化的多点灰色模型在滑坡沉降预测中的应用[J]. 中国地质灾害与防治学报, 2015, 26(2): 3-8. |
| [9] |
刘寒冰, 向一鸣, 阮有兴. 背景值优化的多变量灰色模型在路基沉降预测中的应用[J]. 岩土力学, 2013, 34(1): 173-181. |
| [10] |
刘淑官, 黄声享, 徐北海, 等. 基于无偏灰色马尔科夫链的基坑沉降预测研究[J]. 测绘地理信息, 2015, 40(4): 10-13. |
| [11] |
沈哲辉, 黄腾, 唐佑辉. 灰色马尔科夫模型在大坝内部沉降预测中的应用[J]. 测绘工程, 2015, 24(2): 69-74. |
| [12] |
王磊, 武术静, 李长青. 灰色马尔科夫模型对煤自燃发火预测的研究[J]. 河南理工大学学报(自然科学版), 2015, 34(1): 35-39. |
| [13] |
杨帆, 赵增鹏, 王小兵. 改进灰色马尔科夫模型在基坑预测中的研究[J]. 测绘与空间地理信息, 2017, 40(7): 15-18. |
| [14] |
邹进贵, 肖扬宣, 张士勇. 马尔科夫链改进的ARIMA-BP神经网络模型研究[J]. 测绘地理信息, 2016, 41(4): 32-36. |
| [15] |
龚明, 叶春明. 基于修正灰色马尔科夫链的上海市PM2.5浓度预测[J]. 自然灾害学报, 2016(5): 97-104. |
| [16] |
武术静. 基于灰色马氏链理论的煤自然发火预测研究[D]. 焦作: 河南理工大学, 2014 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D739581
|
 2018, Vol. 43
2018, Vol. 43

