| 半参数AR模型在隧道拱顶沉降分析中的应用 |
2. 河南省有色金属地质矿产局第六地质大队,河南 郑州, 450016
2. Henan Provincial Non-ferrous Metals Geological and Mineral Resources Bureau Sixth Geological Team, Zhengzhou 450016, China
在新奥法隧道施工期间,需要对隧道围岩变形进行严密监测,而隧道拱顶沉降是判断围岩状态的最主要依据,通过对拱顶沉降数据的处理,预报其最终稳定位移,从而确定支护的最佳工作状态和支护结构工艺参数[1]。由于时间序列模型只考虑序列内部的相关关系,对动态数据具有外延的特性[2],同时文献[3]已证明高阶自回归AR模型可代替平稳可逆较复杂的ARMA模型,因此时间序列AR模型在监控数据处理中运用广泛。但传统的时间序列AR模型并未考虑观测过程中由于仪器受到施工机械等影响造成观测数据包含系统误差及建立的预测模型与真实情况的偏差,而半参数模型可以较好地处理系统误差。因此,本文提出以模型误差或观测值系统误差作为未知的非参数分量对AR模型进行补偿,建立半参数AR模型,并基于系统误差的延续性,对模型中的非参数分量进行拟合外推,最终建立顾及系统误差的预报模型。通过对某隧道拱顶的沉降预报表明,该方法可以提高模型拟合预报精度,具有一定的实际应用价值。
1 半参数AR模型| $ {x_t} = {\varphi _1}{x_{t-1}} + {\varphi _2}{x_{t-2}} + \cdots + {\varphi _n}{x_{t-p}} + {a_t} $ | (1) |
式中, xt为平稳观测数据序列;φi(i=1, 2…, p)为自回归参数;at为白噪声序列。对于去除趋势项的平稳时间序列可以采用FPE(final prediction error)定阶准则确定模型的阶数[7],并运用最小二乘原理求解模型的参数。
由于在建模中忽略了观测仪器自身系统误差及外界温度、湿度的影响,同时忽略了依据模型定阶准则建立的AR模型与实际情况的偏差,因此,以模型误差或观测值系统误差作为未知的非参数分量对AR模型进行补偿,然后运用半参数核光滑估计理论进行模型求解。半参数AR模型为[8-10] :
| $ \mathit{\boldsymbol{L = Bx + s}}\left( \mathit{\boldsymbol{t}} \right) + \mathit{\boldsymbol{a}} $ | (2) |
式中,Bx为模型的主体部分,
设式(2)中的s(t)参数化逼近Hr,H为(n-p)×q矩阵,r为q×1附加参数向量,则式(2)改写为:
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{Bx}} + \mathit{\boldsymbol{Hr}} + \mathit{\boldsymbol{a}} $ | (3) |
考虑极小问题满足:
| $ {\left( {\mathit{\boldsymbol{L}}-\mathit{\boldsymbol{B\hat x}}-\mathit{\boldsymbol{H\hat r}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{L}}-\mathit{\boldsymbol{B\hat x}} - \mathit{\boldsymbol{H\hat r}}} \right) = \min $ | (4) |
其最小二乘解满足下列法方程:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B\hat x}} + {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H\hat r}} = {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}}\\ {\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{B\hat x}} + {\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H\hat r}} = {\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{L}} \end{array} \right. $ | (5) |
或
| $ \mathit{\boldsymbol{\hat x = }}{\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{-1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}}-\mathit{\boldsymbol{H\hat r}}} \right) $ | (6) |
| $ \mathit{\boldsymbol{H\hat r}} = {\mathit{\boldsymbol{H}}_s}\left( {\mathit{\boldsymbol{L}}-\mathit{\boldsymbol{B\hat x}}} \right) $ | (7) |
式中,Hs=H(HTH)-1HT为投影阵。如果用任意光滑矩阵S代替Hs,则其解记为:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_\mathit{\boldsymbol{G}}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{-1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}}-{{\mathit{\boldsymbol{\hat s}}}_\mathit{\boldsymbol{G}}}} \right)\\ {{\mathit{\boldsymbol{\hat s}}}_\mathit{\boldsymbol{G}}} = \mathit{\boldsymbol{H\hat r}} = \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{L}}-\mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\hat x}}}_\mathit{\boldsymbol{G}}}} \right) \end{array} \right. $ | (8) |
由式(8)可得[11] :
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_\mathit{\boldsymbol{G}}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\left( {\mathit{\boldsymbol{I}}-\mathit{\boldsymbol{S}}} \right)\mathit{\boldsymbol{B}}} \right)^{-1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\left( {\mathit{\boldsymbol{I}}-\mathit{\boldsymbol{S}}} \right)\mathit{\boldsymbol{L}}\\ {{\mathit{\boldsymbol{\hat s}}}_\mathit{\boldsymbol{G}}} = \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\hat x}}}_\mathit{\boldsymbol{G}}}} \right) \end{array} \right. $ | (9) |
如果取S=S(α)=(K(n-p); ih(ti))(n-p)×(n-p),其中,K(n-p); ih(ti)=K(n-p); ih(ti; tp+1, …, tn)是只与窗宽参数h及tp+1, …, tn有关的核权函数,窗宽参数h由广义交叉核实法确定[12]。则称式(9)的估计为偏核光滑估计。
对于求得的非参数分量,由于其未知性和复杂性,对于非参数分量进行预测有较大的难度,文献[13]也并未给出有效的估计方法,而有理分式函数对复杂的非线性问题可以较好地逼近,其中帕德逼近法是一种简洁而有效的逼近方法[14],因此,本文采用[4/2]阶帕德逼近函数对系统误差进行拟合外推。最终,综合考虑得到半参数AR模型的预报方程为:
| $ {\hat x_t} = {\hat \varphi _1}{\hat x_{t-1}} + {\hat \varphi _2}{\hat x_{t-2}} + \cdots + {\hat \varphi _p}{\hat x_{t-p}} + {\hat s_{t - p}} $ | (10) |
式中,
根据观测数据序列确定模型阶数,并建立AR(p)模型,步骤如下:
1) 按式(1)建立AR(p)模型,由样本自协方差函数计算样本自相关函数和偏相关函数,初步判断模型阶数,并采用FPE定阶准则精确确定模型的阶数;
2) 按式(2)建立半参数AR模型,由半参数核光滑估计理论估计模型参数和非参数分量;
3) 对于得到的(n-p)个非参数分量,运用帕德逼近函数进行拟合外推。
4) 根据求出的参数值及系统误差预测值,建立半参数AR模型预报方程。
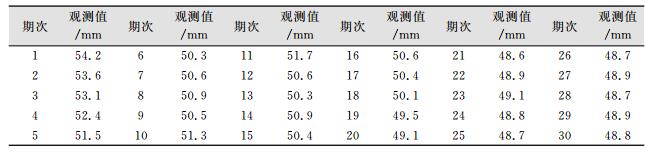
3 实例分析表 1是成贵高铁某隧道某断面拱顶从2014年6月至7月每天进行一期观测获得的一组沉降数据,先利用前25期数据建模,再利用模型对后5期数据进行预报检验分析(为了方便计算,去除数据前5位)。
| 表 1 隧道拱顶沉降数据 Table 1 Tunnel Vault Settlement Data |
 |
从表 1中可以看出,观测序列存在明显的趋势项,采用一阶多项式进行趋势项提取:
| $ f(t) = 53.017-0.183t $ |
制作回归残差序列图如图 1所示。从图 1可看出,其观测序列在均值0上下浮动,初步判定回归残差序列平稳。
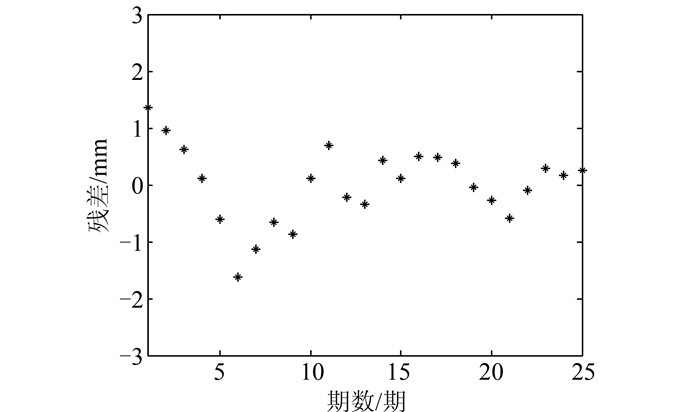 |
| 图 1 回归残差序列图 Figure 1 Regression Residuals Series Graph |
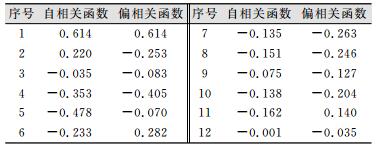
求出平稳序列的自相关函数和偏相关函数,如表 2所示。从表 2可以看出,自相关函数呈拖尾变化,而偏相关函数有明显的截尾现象,取阈值
| 表 2 自相关函数与偏相关函数 Table 2 Auto-correlation Function and Partial Correlation Function |
 |
使用FPE定阶准则定阶:FPE(1)=0.289 8;FPE(2)=0.293 9;FPE(3)=0.316 5;FPE(4)=0.287 0;FPE(5)=0.310 2。由此可见,FPE(4)的值最小,则此模型最佳阶次为4。
根据式(1)建立AR(4)模型,可求解参数:φ1=0.775 0;φ2=-0.440 6;φ3=0.475 3; φ4=-0.531 3。根据预报公式对前21组数据进行1步预报,计算1步拟合中误差为σ1=0.376 0。
根据式(2)建立半参数AR(4)模型, 可求解参数:φ1=0.465 0;φ2=-0.461 2;φ3=0.345 9; φ4=-0.476 6。其中,核函数取
对比两组解算方法的拟合中误差可知,半参数AR模型的拟合精度要优于传统AR模型,说明半参数AR模型能够补偿系统误差,从而建立更加符合实际的参数模型。
对于半参数AR模型求解分离出的系统误差,本实例采用[4/2]阶帕德逼近函数对其进行拟合外推。非参数分量系统误差拟合见图 2。综合考虑系统误差的影响,运用式(10)最终求得半参数AR模型的预报值,并与传统AR模型求得的预报值及实测值进行比较分析,如表 3所示。
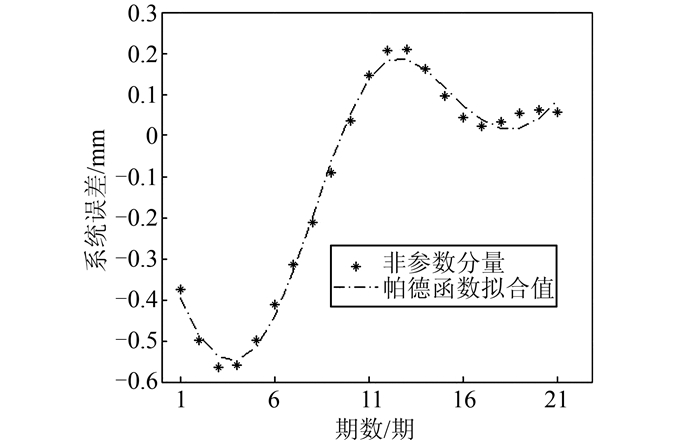 |
| 图 2 非参数分量拟合 Figure 2 Non-parametric Fitting Component |
| 表 3 预报结果对比 Table 3 Comparison Predicted and Observed in Different Method |
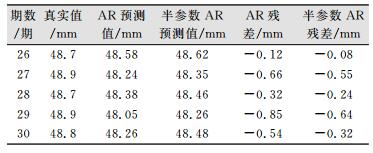 |
从实测数据及两种方法预测结果的对比分析中可以看出:
1) 传统AR模型的预测结果与实测值比较接近,最大误差为0.85 mm,平均误差为0.50 mm,说明AR模型用于沉降预测是有效的;
2) 半参数AR模型的预测结果与实测值更加接近,最大误差为0.64 mm,平均误差为0.37 mm,说明半参数AR模型考虑到系统误差的影响,可以得到更好的建模效果和预测精度。
为了方便对比,现将两种方法的拟合预测残差用图 3表示。由图 3可知, 半参数AR模型得到的残差明显小于传统AR模型的残差,说明通过选择合理的窗宽参数,半参数AR模型可以提高拟合预报精度。
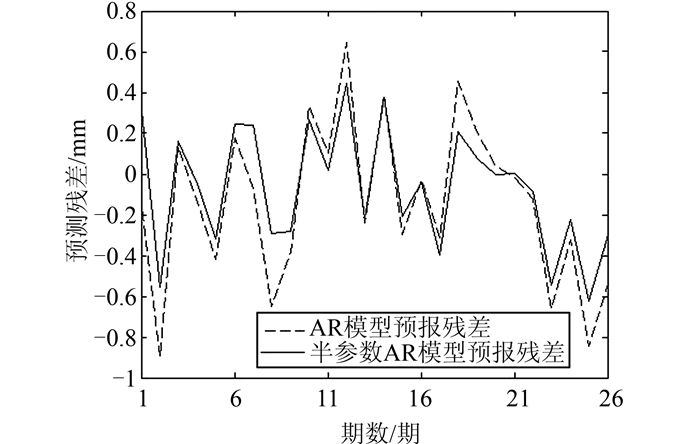 |
| 图 3 两种方法拟合预报残差对比图 Figure 3 Comparison of Fitting Prediction Residuals of Two Methods |
4 结束语
本文通过建立半参数AR模型并将其应用于隧道拱顶沉降数据分析中, 结果表明,半参数AR模型可有效分离出模型误差或观测值系统误差,同时对系统误差进行拟合推估,保证了半参数AR模型具有更好的拟合与预报能力。由于模型误差或观测值系统误差的复杂性,对其进行拟合存在较大的难度,对于如何确定合适的帕德函数的阶数对其加以拟合推估,还值得进一步研究。
| [1] | 蒋建平, 高广运. 基于俞氏四参数模型的隧道拱顶沉降预测[J]. 中国矿业大学学报, 2009, 38(5): 670–674 |
| [2] | 杨叔子, 吴雅, 轩建平. 时间序列分析的工程应用[M]. 2版. 武汉: 华中科技大学出版社, 2007 |
| [3] | 邓自立, 王欣, 高媛. 建模与估计[M]. 北京: 科学出版社, 2007 |
| [4] | 徐北海, 徐旭, 刘淑官, 等. 时间序列分析方法在变形数据处理中的应用研究[J]. 测绘地理信息, 2016, 41(1): 61–65 |
| [5] | 刘娜, 栾元重, 黄晓阳, 等. 基于时间序列分析的桥梁变形监测预报研究[J]. 测绘科学, 2011, 36(6): 46–48 |
| [6] | 石双忠, 岳东杰, 梅红. 时序分析在变形监测数据处理中的应用[J]. 工程勘察, 2004, (3): 59–61 |
| [7] |
林勋. 时间序列分析在建筑物变形监测中的应用[D]. 长春: 吉林大学, 2005 |
| [8] | 李潇, 尹晖. 变形分析中AR模型的精化[J]. 测绘工程, 2008, 17(5): 23–25 |
| [9] | 李秀海, 郭达志. 应用半参数AR模型的电离层TEC建模与预测[J]. 测绘科学, 2011, 36(2): 149–151 |
| [10] | 陶本藻, 陈希龙. 基于模型误差补偿的AR(p)最佳建模方法[J]. 测绘通报, 2005, (8): 8–10 |
| [11] | 丁士俊, 陶本藻. 半参数模型核光滑估计与模拟分析[J]. 大地测量与地球动力学, 2004, 24(4): 24–28 |
| [12] |
丁士俊. 测量数据的建模与半参数估计[D]. 武汉: 武汉大学, 2005 |
| [13] | 许昌, 岳东杰, 董育烦, 等. 基于主成分和半参数的大坝变形监测回归模型[J]. 岩土力学, 2011, 32(12): 3 738–3 741 |
| [14] | 李庆扬, 王能超, 易大义. 数值分析[M]. 5版. 北京: 清华大学出版社, 2008 |
 2018, Vol. 43
2018, Vol. 43

