| 一种基于时空轨迹挖掘的即时配送末端路径指引策略 |
哪个门可以进出小区,且更加便捷?”“14号楼在小区里什么位置?”“小区里这么多小路,我该在哪里转弯?”
以上都是即时配送骑手在进入小区、商场内部面对不够详尽的导航地图时遇到的问题。在整个即时配送物流中,兴趣面(area of interest,AOI)末端是非常重要的环节。它包含了整条配送路径的起点段和终点段,即取餐段(商户)和送餐段(用户),顺利取餐和送餐是配送成功的标志。常规的路径规划、预计到达时间(estimated time of arrival,ETA)服务在高速公路、城市主干道场景下相对成熟、稳定,其预估的距离、时间、路径结果比较准确[1]。而在末端AOI内部,特别是在缺路网、无路网数据的情况下,加上末端道路复杂,导致了骑手寻路的不确定性,距离、时间、路径的预估难度也相应增加,预估准确性较低,进而影响整个订单的预估准确性。因此,要设计科学的方案,为快送订单首尾末端段提供精确的时间、距离、路径预估,并配套设计相应的调用策略,从而为骑手提供良好的末端指引服务,解决即时配送“最后一公里”的问题[2, 3]。
1 即时配送末端指引算法设计即时配送是一种时效性要求更高的物流服务,主要被应用于外卖、闪送等场景[4]。在一个即时配送订单中,往往从AOI中的商户点(取点)出发经过相应的AOI门禁到达用户点(送点)。即时配送流程如图 1所示。
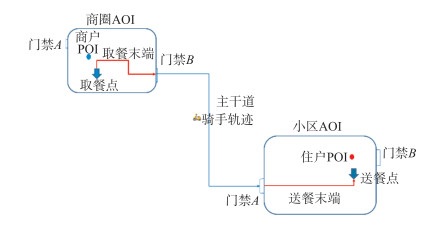 |
| 图 1 即时配送流程 Fig.1 Flow Chart of Instant Delivery |
由于整个末端指引涉及的算法全过程较长,本文将全过程归纳为数据预处理、轨迹召回与切分、距离时间训练与聚合、末端指引路径生成、结果校正与输出5个重要阶段。
1.1 数据预处理末端场景针对的是AOI内部,因此要将取送点召回到所属AOI。为了避免引入过多不必要的数据,可以将AOI和取送点转化为Geohash编码,根据Geohash编码将相同的AOI和取送点进行匹配,根据取送点与AOI空间范围的关系,将取送点归属至对应的AOI,从而获得AOI内部的取送点[5]。
由于不同时间的订单中可能存在相同的取送点,不同用户输入的订单地址也可能是相同的送餐点。因此,为了提取有效数据,可以根据用户输入地址、取送点经纬度坐标对一段时间内(如1个月)的订单取送点进行去重。
1.2 轨迹召回与切分将一定时间段内(如1个月)的每条订单轨迹数据按不同AOI轨迹段进行切分,再根据取送点与轨迹中签到点的最近距离进行判断,召回经过该取送点的AOI内部轨迹。要注意的是,一段AOI内部轨迹中可能包含2个及以上取送点。为了更准确地预估取送点到门禁点的时间和距离,需要剔除中间点(如图 2中的取送点2),只保留首、尾取送点的轨迹(如图 2中的红色线段),避免途经其他点对时间和距离产生影响。
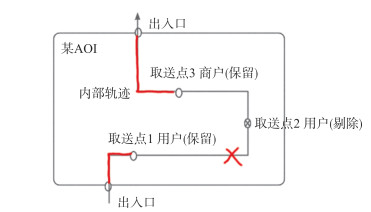 |
| 图 2 轨迹召回 Fig.2 Track Recall |
在获得AOI内部轨迹的基础上,需要更精确地获得该段轨迹进出AOI所对应的门禁点。通过轨迹点与AOI空间范围的位置关系,召回进出AOI的轨迹点,挖掘进出AOI的精确时间。同时,针对召回的进出点,以10 m为半径召回距其最近的AOI门禁点。剔除进出点距离最近AOI门禁点在10 m以上的低质量轨迹,获得完整的AOI进出结构化轨迹数据。
1.3 距离、时间训练与聚合针对各条轨迹中进入AOI门禁点至取送点、离开取送点至门禁点的轨迹段,利用轨迹点所记录的时间戳和空间坐标进行时间与距离计算。根据网格或兴趣点(point of interest,POI)的ID——POI_ID对结果进行聚合,获得距离和时间的预估值。
1)将轨迹的起、终点坐标规整为边长为5 m的网格点,具体表现为将坐标小数点后的第五位归化为0或5,再根据此网格,将起、终点相同的轨迹进行聚合获得距离、时间的均值。空间聚合示例如图 3所示。
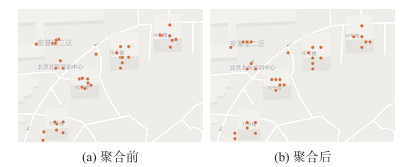 |
| 图 3 空间聚合示例 Fig.3 Diagram of Spatial Aggregation |
2)根据各取送点挂接的POI_ID进行语义聚合,在此基础上,利用具有噪声的基于密度的空间聚类(density-based spatial clustering of applications with noise,DBSCAN)算法进行空间聚合,如图 4所示。召回经过第一簇的轨迹,剔除其他低质量轨迹,计算召回轨迹的距离、时间的均值。利用该方法得到的结果数据量更小,但只适用于那些有POI_ID的信息的取送点[6]。
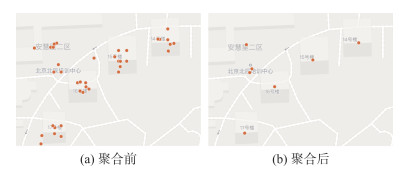 |
| 图 4 语义聚合 Fig.4 Semantic Aggregation |
1.4 末端指引路径生成
对召回的各取送点与门禁点间的时空轨迹数据进行如下处理:
1)轨迹压缩与序列化,基于时间戳的轨迹,采用秒级记录会导致骑手的时空轨迹数据量非常大,增加计算复杂度。因此,要对轨迹进行压缩,在不明显影响轨迹数据精度的情况下,减小轨迹数据量。本文采用Douglas-Peucker算法进行轨迹压缩,实验结果表明,利用该算法能够压缩数据量,同时保留了轨迹的行走拐弯细节,轨迹压缩效果如图 5所示。序列化则是将轨迹转换为一个个标准单元,方便后续的轨迹聚类等处理工作[7]。
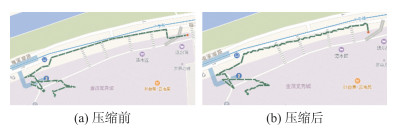 |
| 图 5 轨迹压缩效果示例 Fig.5 Diagram of Trajectory Compression |
2)高频次轨迹聚合。不同取送点的订单频次差别巨大,因此,在同一段时间内,不同取送点可召回的轨迹数量也有高有低。针对高低频次轨迹,采用不同方案进行处理。利用轨迹聚合生成路径,轨迹必须达到一定的数量。基本思路是,在大量序列化轨迹中求起点与终点间的最短路径,如图 6所示。
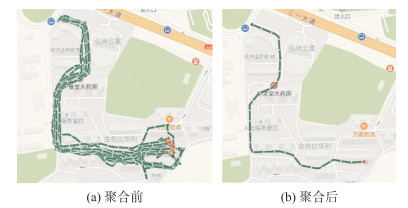 |
| 图 6 轨迹聚合 Fig.6 Trajectory Aggregation |
3)低频次轨迹选优。当起点与终点之间轨迹数量稀少,不足以利用聚合生成路径时,需要从中选择高质量代表性轨迹。骑手实际行走过程中,经常会徘徊绕路,导致轨迹出现重叠,产生重合点。轨迹的重合点数量在一定程度上标志了轨迹的质量。将轨迹按照其重合点数进行排序,选取重合点最少、质量最佳的轨迹[8],如图 7所示。
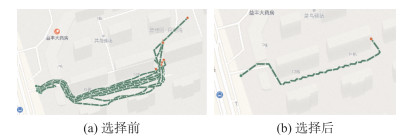 |
| 图 7 代表性轨迹选择 Fig.7 Selection of Representative Trajectories |
1.5 结果校正与输出
根据重合点确定末端指引路线质量标准:路线重合点数小于10,且单位长度(m)重合点数小于0. 1。轨迹校正流程如图 8所示。
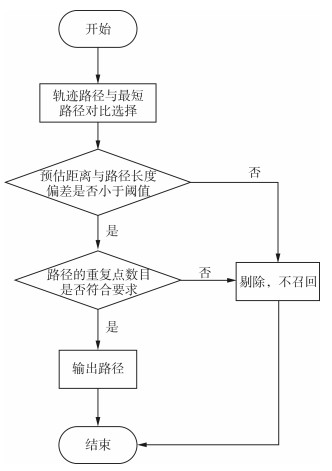 |
| 图 8 轨迹校正 Fig.8 Trajectory Correction |
剔除低质量路径,选择高质量路径,形成最终可交付应用的成果[9]。图 9展示了末端指引路线的示例。
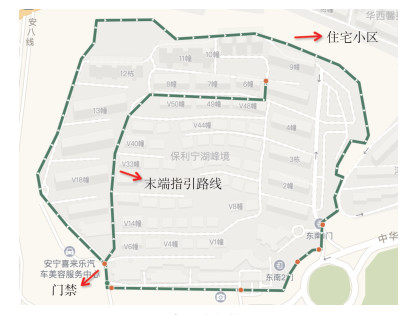 |
| 图 9 末端路径指引示例 Fig.9 Example of End Path Guidance |
2 应用策略设计与应用效果 2.1 应用策略设计
本文的算法成果在线上实际应用时,遵循如下调用策略:
1)输入POI_ID或取送点网格及进出类型进行检索,获取取送点与AOI各个可通行门禁点之间的精确预估距离、时间和路径[10]。
2)订单完整指引路径的生成与组合。
① 当起、终点AOI均只有一个门禁时,将两端的末端路径与主干道路径拼接起来,形成完整的订单路径。
② 当起、终点AOI存在多个可通行门禁时,在多个门禁组合中,选取路径总距离最小的方案。
2.2 应用效果分析重点城市使用该策略前后的AOI内部路线的距离准确性和路径相似度(以高质量实走轨迹为评测集),发现使用该策略后,100 m以内的距离偏差占比提升3%,0. 75以上的路径相似度占比提升8%。
3 结束语近年来,业界出现了一些利用GPS测绘、影像识别、激光点云扫描等方式补充末端道路以及利用历史轨迹构建虚拟道路的方法,来完善AOI末端路网,进而完善相应道路的权重数据,同时提高数据更新频率,能够在一定程度上克服手机导航地图不够精细的缺点,提升末端指引的体验。但目前来说,该方法存在规模大、周期长等缺点,短期内难以大规模应用。
时空数据是智慧应用的底座[11]。本文的关键在于,基于历史时空轨迹挖掘,克服传统导航地图末端不详细、通行状态更新不及时等缺点。关键技术策略可总结为:
1)基于时空轨迹的距离时间挖掘方法。通过对时空轨迹的召回、切分与计算,挖掘取送点与门禁的通行距离与耗费时间,提升路径导航时预估整体距离和时间的准确性。
2)基于空间与语义的POI双聚合方法。在DB⁃ SCAN算法的基础上,加入POI_ID语义信息,实现POI空间、语义的双重聚合。
3)基于时空轨迹的末端路线生成策略。针对不同数量的轨迹,分别采用轨迹聚合与代表性轨迹选取生产末端指引路线。
4)末端指引调用与择优策略。基于轨迹挖掘的算法成果,设计配套的调用策略,保证了最优方案的选择。
| [1] |
张锦, 陈义友. 物流"最后一公里"问题研究综述[J]. 中国流通经济, 2015, 29(4): 23-32. |
| [2] |
杜清运, 任福. 空间信息的自然语言表达模型[J]. 武汉大学学报·信息科学版, 2014, 39(6): 682-688. |
| [3] |
陈思远. 基于改进后的地图匹配算法及Dijkstra算法的动态路径优化问题的研究[D]. 上海: 东华大学, 2018
|
| [4] |
辜勇, 柳悦, 陈句, 等. 即时配送问题研究综述[J]. 中国物流与采购, 2021(15): 34-35. |
| [5] |
金安, 程承旗, 宋树华, 等. 基于Geohash的面数据区域查询[J]. 地理与地理信息科学, 2013, 29(5): 31-35. |
| [6] |
李琦, 林志勇. 顾及空间及语义相关性的POI位置标注优化方法[J]. 地球信息科学学报, 2022, 24(7): 1 254-1 263. |
| [7] |
Douglas D H, Peucker T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. Cartographica: The International Journal for Geographic Information and Geovisualization, 1973, 10(2): 112-122. DOI:10.3138/FM57-6770-U75U-7727 |
| [8] |
Mattila P. Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability[M]. New York: Cambridge University Press, 1995.
|
| [9] |
杜豫川, 都州扬, 师钰鹏, 等. 路侧感知车辆轨迹数据质量智能评估方法[J]. 中国公路学报, 2021, 34(7): 164-176. |
| [10] |
叶文娟, 艾廷华. 多维度轨迹数据的SQL时空查询方法[J]. 测绘地理信息, 2017, 42(6): 16-20. |
| [11] |
王聪. 基于时空信息模型的智慧城市数字底座设计初探[J]. 测绘地理信息, 2021, 46(S1): 162-164. |
 2023, Vol. 48
2023, Vol. 48

