| 多线地面激光扫描仪误差分析及自标定 |
2. 浙江省测绘大队,浙江 杭州,310030
2. The Institution of Geological Surveying and Mapping, Hangzhou 310030, China
多线地面激光扫描仪由于其外形小、成本合理、能提供实时三维扫描结果等特点,近年来在测绘行业得到了广泛的应用与关注。作为高分辨率点云数据的主要采集装置,激光扫描仪已被集成到无人机、车载移动测量系统、SLAM(simultaneous localization and mapping)系统等领域中[1]。某些高精度测绘领域对扫描仪的精度要求很高,如隧道变形监测[2]、动车组开闭罩外形曲面检测[3]、物体表面裂纹识别[4]等。此外,受周围环境及使用时间的影响,仪器的精度会随之发生变化。因此,需要分析扫描仪的误差来源,并对其进行标定以减小系统误差,从而改善仪器获取点云数据的质量。其中,自标定方法因其“不需借助其他测绘仪器”的独特优势,在近年来引起广大研究者的关注。
对系统误差进行自标定,是指在不借助任何外界特殊设备情况下,实现仪器标定参数的最优化估计[5]。根据标定目标的类型,现有自标定方法可分为基于点自标定方法、基于平面自标定方法、基于圆柱面自标定方法3种。
Lichti等[6]提出了一种构建信号点网络的自标定方法,通过调整网络节点的位置,同时优化求解Faro 880扫描仪的内参和外参;Rietdorf等[7]用平面参数代替标定模型中的坐标点,借助四元数变换扩展的高斯马尔科夫模型,通过调整目标点云所在平面的位置,求解标定参数;Chan等[8]利用柱状物体替代平面特征约束,借助三维圆柱模型实现Velodyne HDL-32E扫描仪系统误差的标定;官云兰等[9]以空间相似变换为基础,构建了具有11个参数的自检校误差模型,对徕卡HDS3000扫描仪的系统误差进行标定。
3种方法共同点均为构造强大几何布局网络,利用点云之间的高冗余性优化求解标定参数。但是,基于点自标定方法会导致参数之间出现高度相关性,影响标定精度[10]。基于圆柱面自标定方法对标定场地有特殊要求,室内场需有管道等圆柱状物体,室外场需有路灯杆等作为约束面。而基于平面自标定方法除了要求标定场包含“平面特征物体”之外,不再需要其他特殊设施。相对于基于点自标定方法而言,其效果更好。相对于基于圆柱面的自标定方法而言,其过程更为简单、可操作性更强。
综上所述,本文采用了一种基于平面约束的非线性最小二乘自标定方法,实现对多线地面激光扫描仪系统误差的自标定。首先,详细分析多线扫描仪的误差来源并确定标定模型;其次,以VLP-16扫描仪为例进行仿真模拟实验,验证实验方案的合理性及模型的有效性;接着,根据该方案进行VLP-16的实测验证,优化求解待标定参数;最后,对标定结果进行精度评定。
1 多线地面激光扫描仪误差分析及自标定现有的多线扫描仪产品众多,对于结构相似的产品,其误差来源及标定方法大同小异。本文主要以VLP-16为例开展多线地面激光扫描仪的自标定工作。相同观测条件下,仪器系统误差的数值大小是按某种规律变化的。根据这一特点,本文重点分析系统误差的产生原因,并建立数学模型对其进行改正。VLP-16的原始观测值有观测距离和测量角度两种。本文将从距离和角度两个方面分析系统误差来源。
1.1 观测距离观测距离是指仪器中心到观测目标之间的水平距离,其系统误差项包括测距乘常数和测距加常数。其中,测距乘常数近似于1,且其数值大小与测量距离呈正相关。假设测量距离100 m时偏移6 cm,则该数值约为1.000 6。仪器标称精度为±3 cm,说明VLP-16测距乘常数与1更接近。另外,仪器采集数据时,其大小波动极不明显,无法对其数值进行可靠估计。特别地,测距乘常数与测距加常数之间的相关系数高达0.754[11]。因此本文不再标定测距乘常数。
测距加常数是指因电路信号延迟、仪器偏心等综合影响而构成的附加常数。当扫描角度固定后,该误差在水平和竖直方向上的影响往往存在着较大的差异,如图 1所示。图 1中,以激光发射器i为例,A、B分别为竖直和水平约束平面;Ri为测量距离;Div、Dih均为测距加常数误差。
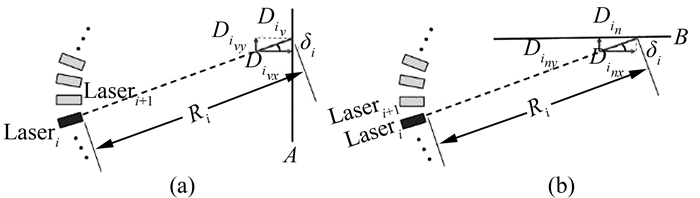 |
| 图 1 测距加常数误差 Fig.1 Distance Offset Error |
对Div按水平和竖直方向进行投影分解:
| $ {D_{{i_{vx}}}} = {D_{{i_v}}} \times \cos \left( {{\delta _i}} \right) $ | (1) |
| $ {D_{{i_{vy}}}} = {D_{{i_v}}} \times \sin \left( {{\delta _i}} \right) $ | (2) |
对Dih按水平和竖直方向进行投影分解:
| $ {D_{{i_{hx}}}} = {D_{{i_h}}} \times \cos \left( {{\delta _i}} \right) $ | (3) |
| $ {D_{{i_{hy}}}} = {D_{{i_h}}} \times \sin \left( {{\delta _i}} \right) $ | (4) |
式中,Divy、Dihx分量会导致目标点在对应平面内发生偏移,而Divx、Dihy分量对点云厚度有较大影响。本文以“目标点到约束平面距离残差值最小”为原则,对约束平面两侧目标点进行点位调整。理论上,目标点离约束平面越远,调整波动越大,效果越好。因此,下面将重点分析对厚度影响较大的分量,即Divx、Dihy。
由于仪器竖直角范围为-15°~15°,故Divx>Dihy。因此,相对于水平方向而言,测距加常数误差在竖直方向的影响更为显著。
1.2 测量角度理想情况下,仪器的竖直轴、水平轴、视准轴均互相垂直,且正交于某个公共点[12],但实际使用时,由于系统误差的存在,原本正交的轴会出现偏移、倾斜,包括竖直轴误差、视准轴误差。下面将仪器水平放置,从这两方面分析测量角度的系统误差。
1.2.1 竖直轴误差仪器的竖直轴与水平轴之间的非正交产生竖直轴旋转误差,如图 2所示。
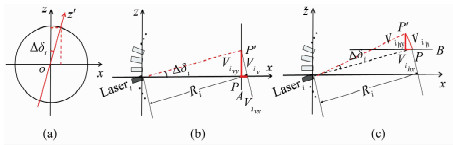 |
| 图 2 竖直轴旋转误差 Fig.2 Vertical Axis Rotation Error |
图 2中,Δδi为竖直角旋转改正误差;P为目标点;P′为实际观测点;Viv、Vih分别为Δδi在竖直和水平面内引起的点位坐标的偏移量。其他变量的指代见上文,下同。
对Viv按水平和竖直方向进行投影分解:
| $ {V_{{i_{vx}}}} = {R_i} \times \left[ {1 - \cos \left( {\Delta {\delta _i}} \right)} \right] $ | (5) |
| $ {V_{{i_{vy}}}} = {R_i} \times \sin \left( {\Delta {\delta _i}} \right) $ | (6) |
对Vih按水平和竖直方向进行投影分解:
| $ {V_{{i_{hx}}}} = {V_{{i_h}}} \times \sin \left( {\frac{1}{2}\Delta {\delta _i}} \right) = {R_i} \times \left[ {1 - \cos \left( {\Delta {\delta _i}} \right)} \right] $ | (7) |
| $ {V_{{i_{hy}}}} = {V_{{i_h}}} \times \cos \left( {\frac{1}{2}\Delta {\delta _i}} \right) = {R_i} \times \sin \left( {\Delta {\delta _i}} \right) $ | (8) |
其中,Vivy、Vihx分量会导致目标点在对应平面内发生偏移,而Vivx、Vihy分量对点云厚度的影响更大。因此,本文重点分析后者。
当Δδi≈0时,若距离Ri相等,则Vihy≫Vihx。而竖直角的范围为-15°~15°,相比于Ri而言,竖直角非常小,使得Δδi也很小。因此,相对于水平方向而言,该误差对点云厚度的影响并不明显。
仪器竖直轴与视准轴的交点在竖直方向发生偏移产生竖直轴偏移误差,如图 3所示。图 3中,ΔV为竖直轴偏移量。竖直轴偏移误差会导致整体点云在竖直方向上发生平移,水平方向无变化。
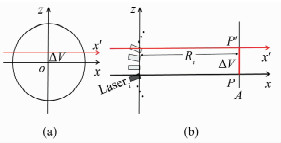 |
| 图 3 竖直轴偏移误差 Fig.3 Vertical Axis Offset Error |
1.2.2 视准轴误差
仪器的视准轴与水平轴之间的非正交产生视准轴旋转误差,如图 4所示。图 4中Δεi为视准轴旋转误差;Hivx、Hih均为Δεi引起的点位坐标的偏移量。Hivy=0,Δεi对竖直面A点云数据在竖直方向上没有影响。对水平方向分量Hivx投影分解:
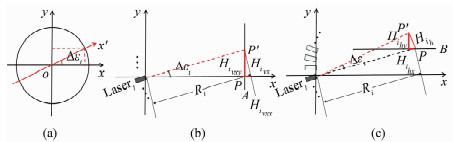 |
| 图 4 视准轴旋转误差 Fig.4 Collomation Axis Rotation Error |
| $ {H_{{i_{uxx}}}} = {R_i} \times \left[ {1 - \cos \left( {\Delta {\varepsilon _i}} \right)} \right] $ | (9) |
| $ {H_{{i_{vxy}}}} = {R_i} \times \sin \left( {\Delta {\varepsilon _i}} \right) $ | (10) |
对Hih按水平和竖直方向进行投影分解:
| $ {H_{{i_{hx}}}} = {H_{{i_h}}} \times \sin \left( {\frac{1}{2}\Delta {\varepsilon _i}} \right) = {R_i} \times \left[ {1 - \cos \left( {\Delta {\varepsilon _i}} \right)} \right] $ | (11) |
| $ {H_{{i_{hy}}}} = {H_{{i_h}}} \times \cos \left( {\frac{1}{2}\Delta {\varepsilon _i}} \right) = {R_i} \times \sin \left( {\Delta {\varepsilon _i}} \right) $ | (12) |
其中,Hivxy、Hihx会导致点云在水平面内发生偏移。而Hivxx、Hihy对点云厚度影响更大。因此,本文将重点分析Hivxx、Hihy。
当Δεi≈0时,若距离Ri相等,则Hihy≫Hivxx,即水平方向的点云对厚度影响更为显著。
仪器的视准轴与水平轴的交点发生偏移产生视准轴偏移误差,如图 5所示。其中,ΔH为视准轴偏移量。视准轴偏移误差会导致整体点云在水平方向上发生平移,竖直方向无变化。
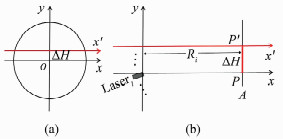 |
| 图 5 视准轴偏移误差 Fig.5 Collomation Axis Offset Error |
综上所述,单独采用水平、竖直、或倾斜方向上的单个数据层,均无法实现准确而有效的标定。因此,在设计标定实验方案时,可采取基于多个数据层的方法,如增加倾斜设站、采用倾斜标定板、多站数据联合标定等。
1.3 多线地面激光扫描仪自标定扫描仪坐标系下的目标点坐标为(Ri, αi, βi)。为统一计算,本文将其转换到笛卡尔直角坐标系下进行优化求解:
| $ \left\{ {\begin{array}{*{20}{l}} {x = {R_i}\cos {\alpha _i}\cos {\beta _i}}\\ {y = {R_i}\cos {\alpha _i}\sin {\beta _i}}\\ {z = {R_i}\sin {\beta _i}} \end{array}} \right. $ | (13) |
式中,i为激光发射器编号,Ri为测量距离,αi为竖直角度值,βi为水平旋转角,(x, y, z)为目标点的笛卡尔坐标。
本文采用以下模型对测距加常数Di、竖直轴旋转误差δi及视准轴旋转误差εi(简称内参)进行标定。测距乘常数不标定原因在上文已说明。实验过程中,仪器倾斜了15°,但该角度大小只是相对于水平地面而言,对于整个标定系统,还不足以完全分离角度误差和偏移误差之间的影响。因此本文不再标定这两个参数。
| $ \left\{ \begin{array}{l} x = \left( {{R_i} + {D_i}} \right) \times \cos \left( {{\alpha _i} + {\delta _i}} \right) \times \left[ {\sin \left( {{\beta _i}} \right) \times } \right.\\ \;\;\;\;\;\;\left. {\cos \left( {{\varepsilon _i}} \right) - \cos \left( {{\beta _i}} \right) \times \sin \left( {{\varepsilon _i}} \right)} \right]\\ y = \left( {{R_i} + {D_i}} \right) \times \cos \left( {{\alpha _i} + {\delta _i}} \right) \times \left[ {\cos \left( {{\beta _i}} \right) \times } \right.\\ \;\;\;\;\;\;\left. {\cos \left( {{\varepsilon _i}} \right) + \sin \left( {{\beta _i}} \right) \times \sin \left( {{\varepsilon _i}} \right)} \right]\\ z = \left( {{R_i} + {D_i}} \right) \times \sin \left( {{\alpha _i} + {\delta _i}} \right) \end{array} \right. $ | (14) |
由于系统误差的存在,目标点均分布在某一平面上或平面两侧。因此,本文将“共面”作为约束条件,对目标点位置进行调整。其中,gk=[g1, g2, g3, g4]T为点云所在平面k的先验未知平面参数值,r=(x, y, z)为物方空间直角坐标系下的点云坐标。
| $ \left( {{\mathit{\boldsymbol{g}}_k},\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{r}}\\ 1 \end{array}} \right]} \right) = 0 $ | (15) |
在静态标定场景中,所有测站点云不在同一坐标系统下。本文采用非线性Gauss Helmert模型实现坐标转换,该模型能够有效避免系数矩阵固定列的影响[13-18]。以站点1为基准,依次将第j站(j=2, 3, 4…)的扫描仪站点坐标i转换到该坐标系下:
| $ \mathit{\boldsymbol{r}} = \mathit{\boldsymbol{R}}(\omega ,\varphi ,\kappa ){\mathit{\boldsymbol{I}}_{ij}} + {\mathit{\boldsymbol{t}}_j} $ | (16) |
式中,R(ω, φ, κ)为旋转变换矩阵,ω、φ、κ分别为绕X、Y、Z轴的旋转角; Iij为点i在扫描仪空间j下的坐标; tj为平移矩阵。R、Iij、tj简称为外参。
2 多线地面激光扫描仪标定实验本文采用控制变量法利用正态分布随机生成点云,利用不同场景获取的多组点云数据进行自标定模拟实验,分析系统误差的影响。模拟标定场大小为10 m×6 m×3 m(长×宽×高)如图 6(a)、6(c)所示。
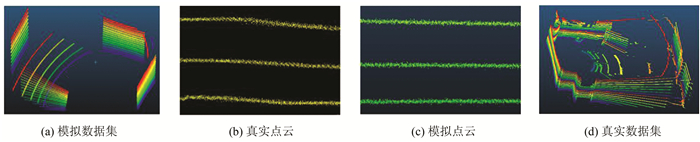 |
| 图 6 实验数据集 Fig.6 Experimental Datasets |
本文选用真实房间作为标定场地以进行实测验证,如图 6(b)、6(d)所示。房间大小为12 m×6 m×3.3 m(长×宽×高),且房间内布设一定数量的倾斜白板,依次将扫描仪架设在房间内不同位置采集数据。假定扫描仪在任一位置均近似水平,分别将仪器绕其竖直轴旋转两次,完成水平0°、180°方向扫描。然后,再将仪器倾斜15°进行二次扫描。
2.1 模拟实验1) 定性分析。模拟实验结果如图 7所示,其中横坐标表示点号,纵坐标表示点到平面的距离,上组图和下组图分别由竖直面内、水平面内的点云计算得到。可以看出,测距加常数在竖直面内分量较水平面大,竖直轴旋转误差、视准轴旋转误差在竖直面内影响较水平面内小,该现象验证了前文误差分析部分的结论。
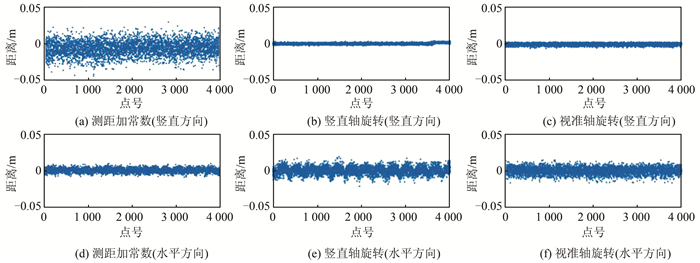 |
| 图 7 系统误差影响对比 Fig.7 Comparison of Systematic Error Effects |
根据上述实验结果及经验,本文总结出了一套较好的多线地面三维激光扫描仪的自标定实验方案,并依据此方案进行了VLP-16扫描仪自标定模拟实验。
2) 定量分析。以仪器内参为例,表 1统计了模拟实验标定前系统误差参数的真值及标定后的优化求解值,并计算两者的差值,可以发现其差值与零非常接近,进一步说明了该方案的有效性。
| 表 1 标定前后内参差值 Tab.1 Difference of Internal Orientation Parameters Before and After Calibration |
 |
2.2 实测验证
(1) 定性分析。图 8统计了实测验证中每个激光发射器在所有约束平面上的扫描点数。在实测验证中,16个激光发射器扫描的点云都参与了标定,且每个激光发射器扫描到的点数均在4万左右,这表明大约有4万组方程用于最优目标函数的求解。
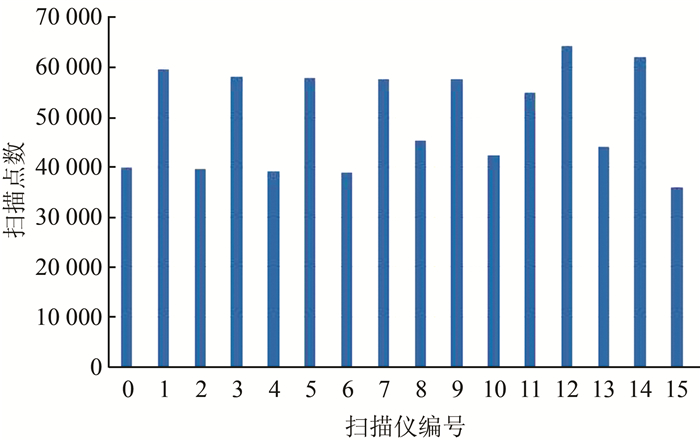 |
| 图 8 扫描点数统计 Fig.8 Number of Points Captured by Each Laser |
(2) 定量分析。VLP-16系统误差参数的优化求解结果中,内参为VLP-16扫描仪16个激光发射器系统误差的均值,平面参数为3组实验数据平面参数的均值。
内参为:
| $ {D_{均值}} = 0.014\;7{\rm{m}} $ |
| $ {\delta _{均值}} = 0.125\;{4^ \circ } $ |
| $ {\varepsilon _{均值}} = 0.053\;{2^ \circ } $ |
外参为:
| $ {\mathit{\boldsymbol{R}}_1} = \left[ {\begin{array}{*{20}{l}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right];{\mathit{\boldsymbol{t}}_1} = \left[ {\begin{array}{*{20}{l}} 0\\ 0\\ 0 \end{array}} \right]; $ |
| $ {\mathit{\boldsymbol{R}}_2} = \left[ {\begin{array}{*{20}{c}} { - 0.998}&0&0\\ 0&{ - 0.999}&0\\ 0&0&{0.998} \end{array}} \right];{\mathit{\boldsymbol{t}}_2} = \left[ {\begin{array}{*{20}{c}} { - 0.007}\\ {0.003}\\ {0.006} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{R}}_3} = \left[ {\begin{array}{*{20}{c}} {0.797}&{ - 0.516}&{0.313}\\ {0.533}&{0.845}&{0.037}\\ { - 0.284}&{0.137}&{0.949} \end{array}} \right];{\mathit{\boldsymbol{t}}_3} = \left[ {\begin{array}{*{20}{c}} { - 0.154}\\ { - 0.036}\\ {0.049} \end{array}} \right] $ |
平面参数为:
| $ {\mathit{\boldsymbol{g}}_{k1}} = {\left[ {\begin{array}{*{20}{c}} { - 0.983}&{ - 0.185}&{ - 0.006}&{1.589} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{g}}_{k2}} = {\left[ {\begin{array}{*{20}{c}} { - 0.187}&{0.982}&{ - 0.008}&{2.452} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{g}}_{k3}} = {\left[ {\begin{array}{*{20}{l}} {0.193}&{ - 0.981}&{ - 0.001}&{2.788} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{g}}_{k4}} = {\left[ {\begin{array}{*{20}{c}} {0.981}&{0.192}&{ - 0.012}&{6.175} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{g}}_{k5}} = {\left[ {\begin{array}{*{20}{c}} {0.332}&{0.918}&{0.218}&{2.471} \end{array}} \right]^{\rm{T}}} $ |
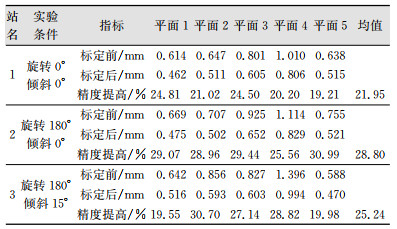
本文采用点到面距离的均方根误差(root mean square error,RMSE)来衡量观测值与真值的偏差。为确保结果的差异完全来自于VLP-16内部的系统误差,本文使用相同测站、相同约束平面,分别计算了所有平面标定前后的RMSE值,并进行对比分析,如表 2所示。可以看出,标定前平面RMSE很大,但经过标定后,RMSE变小,更加接近于0,说明点云所在平面的厚度变薄,VLP-16的系统误差几乎被完全消除,点云数据的质量得到明显改善。
| 表 2 标定前后RMSE对比 Tab.2 Comparison of RMSE Before and After Calibration |
 |
由于扫描仪系统误差的存在,点云并非分布在某一平面上,而是零散的分布在约束平面的两侧,且点到面距离总体呈正态分布。理论上,点到约束平面的距离越小,平面越薄。表 3统计了标定前后点到平面距离的最小值、最大值及均值。
| 表 3 标定前后距离统计/cm Tab.3 Distance Statistics Before and After Calibration/cm |
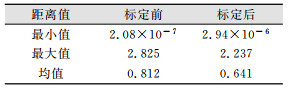 |
表 3表明目标点到约束平面的距离整体缩小约30%。更直观地,本文将标定前后的距离值以散点图(图 9(a))、直方图(图 9(b))的形式进行了可视化。
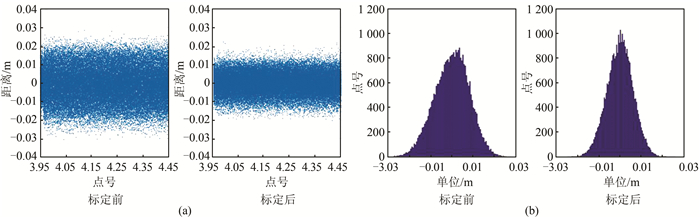 |
| 图 9 标定前后距离可视化结果 Fig.9 Distance Visualization Results Before and After Calibration |
从图 9中可以看出,标定前后所有点均分布在拟合平面的两侧,且点到约束平面的距离在3 cm以内,这与VLP-16的标称测距精度3 cm是相符的。图 9(a)表明,标定后点到约束平面的距离明显变小。图 9(b)表明,经过标定,点云的分布与拟合平面更加接近,距离的变化范围从-3~3 cm缩小到-2~2 cm。这一现象说明,本文所采用的基于平面约束的非线性最小二乘自标定模型是非常有效的。同时,点到面距离呈正态分布在图 9(b)中得到了验证。
3 结束语本文从多线地面激光扫描仪的构造及工作原理出发,详细分析了多线扫描仪的误差来源,并采用基于平面约束的非线性最小二乘静态自标定模型对仪器的系统误差进行标定。该模型适用于现有的绝大多数多线地面激光扫描仪,具有一定的普遍性。本文以多线扫描仪VLP-16为例,采用该标定模型分别进行了自标定的模拟实验及实测验证。实验结果表明,通过标定,扫描仪所采集的点云到约束平面距离变化范围从-3~3 cm缩小为-2~2 cm。相对于厂家的标称精度3 cm而言,精度提高了30%以上。此外,本文方法使得标定后整体估计的RMSE提高了20%~30%。在未来工作中,将对多线激光扫描仪的系统误差项进行更为细致的分析,旨在尽可能地消除扫描仪的所有系统误差。
| [1] |
Toth C, Józków G. Remote Sensing Platforms and Sensors:A survey[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2016, 115: 22-36. |
| [2] |
袁长征, 滕德贵, 胡波, 等. 三维激光扫描技术在地铁隧道变形监测中的应用[J]. 测绘通报, 2017(9): 160-161. |
| [3] |
赵峻松, 尹志春, 朱文战, 等. 激光扫描仪在动车组开闭罩外形曲面检测中的应用[J]. 广东科技, 2017(4): 83-85. DOI:10.3969/j.issn.1006-5423.2017.04.025 |
| [4] |
Laefer D F, Truong-Hong L, Carr H, et al. Crack Detection Limits in Unit Based Masonry with Terrestrial Laser Scanning[J]. NDT&E International, 2014, 62(2): 66-76. |
| [5] |
Lichti D D. Terrestrial Laser Scanner Self-Calibration:Correlation Sources and Their Mitigation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(1): 93-102. DOI:10.1016/j.isprsjprs.2009.09.002 |
| [6] |
Lichti D D. Error Modelling, Calibration and Analysis of an AM-CW Terrestrial Laser Scanner System[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2007, 61(5): 307-324. DOI:10.1016/j.isprsjprs.2006.10.004 |
| [7] |
Rietdorf A, Gielsdorf F, Gruendig L.A Concept for the Calibration of Terrestrial Laser Scanners[C].Proceedings FIG Working Week (on CD-ROM), International Federation of Surveyors, Athens, Greece, 2004
|
| [8] |
Chan T O, Lichti D D. Automatic in Situ Calibration of a Spinning Beam LiDAR System in Static and Kinematic Modes[J]. Remote Sensing, 2015, 7(8): 10480-10500. DOI:10.3390/rs70810480 |
| [9] |
官云兰, 程效军, 詹新武, 等. 地面三维激光扫描仪系统误差标定[J]. 测绘学报, 2014, 43(7): 731-738. |
| [10] |
Chow J C K, Lichti D D, Glennie C. Point-Based Versus Plane-Based Self-Calibration of Static Terrestrial Laser Scanners[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2011, 38(5/12): 121-126. |
| [11] |
Glennie C, Lichti D D. Static Calibration and Analysis of the Velodyne HDL-64E S2 for High Accuracy Mobile Scanning[J]. Remote Sensing, 2010, 2(6): 1610-1624. DOI:10.3390/rs2061610 |
| [12] |
Lichti D D. A Review of Geometric Models and Self-Calibration Methods for Terrestrial Laser Scanners[J]. Boletim de Ciencias Geodesicas, 2010, 16(1): 3-19. |
| [13] |
刘春阳.三维坐标转换的Gauss-Helmert模型及其抗差解法[D].合肥: 安徽理工大学, 2016
|
| [14] |
刘超, 王彬, 赵兴旺, 等. 三维坐标转换的高斯-赫尔默特模型及其抗差解法[J]. 武汉大学学报·信息科学版, 2018, 43(9): 1320-1327. |
| [15] |
刘春阳, 刘超. 三维坐标转换的非线性Gauss-Helmert模型及其解法[J]. 测绘科学, 2017(5): 122-127. |
| [16] |
曾文宪, 陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报·信息科学版, 2003, 28(5): 566-568. |
| [17] |
邱德超, 鲁铁定. 基于Partial EIV模型的三维坐标转换参数求解方法[J]. 江西科学, 2017(3): 355-359. |
| [18] |
王东阁, 邱卫宁, 王刘准, 等. 基于partial-EIV模型的WTLS算法在三维坐标变换中的应用[J]. 测绘地理信息, 2015, 40(5): 8-12. |
 2019, Vol. 44
2019, Vol. 44


