| 北斗卫星多路径系统偏差改正的研究 |
2. 武汉大学测绘学院,湖北 武汉,430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
北斗卫星导航系统(BeiDou navigation satellite system,BDS)是中国自主研发独立运行的卫星导航系统,为各类用户提供高精度高质量的服务,并能向拥有更高要求的授权用户提供进一步的服务。从2000年北斗卫星导航实验系统建成至今,北斗卫星导航定位系统已经实现亚太地区的全面覆盖,独立为亚太地区提供导航、定位授时等服务,并计划在2020年完成北斗卫星全球定位系统的构建。
北斗卫星多路径系统偏差由Hauschild等首次提出,他发现这种仅存在于北斗卫星导航系统中的系统偏差导致伪距观测值与载波相位观测值之间的差异超过1 m[1]。同年,Perello等相继发现了北斗多路径系统偏差的存在,发现该偏差的大小与卫星高度角相关[2]。文献[3, 4]在研究北斗卫星区域导航系统和国际GNSS服务中再次证明了北斗多路径系统偏差,发现北斗多路径系统偏差被证明是高度角相关系统误差,不同频率下的多路径系统偏差有显著区别,并确认这种误差源来自于北斗卫星内部的多路径效应[3]。Wanninger等利用20 d的观测数据建立了北斗卫星多路径系统偏差改正的分段线性经验公式[5],本文在此基础上,选择多项式拟合的方法,通过2015年半年的数据对北斗卫星伪距多路径偏差建立多项式改正模型,增大了数据量,并精简了改正模型,最终通过MP(multipath combination)序列系统偏差的改正效果以及SPP(single point positioning)的结果验证其有效性。
1 北斗卫星多路径系统偏差在GNSS测量过程中,来自卫星的直射信号与经过测站附近物体的反射信号在接收机天线相位中心产生干涉,从而使观测值偏离真值,这种误差称为多路径误差[6]。利用载波相位观测值和伪距观测值联立变换可以得到伪距多路径误差MP组合公式如下:
| $ \left\{ \begin{array}{l} {M_{p{\rm{1}}}} = {p_1} - \frac{{{f_1}^2 + {f_2}^2}}{{{f_1}^2 - {f_2}^2}}{\phi _1} + \frac{{2{f_2}^2}}{{{f_1}^2 - {f_2}^2}}{\phi _2}\\ {M_{p{\rm{2}}}} = {p_2} - \frac{{2{f_1}^2}}{{{f_1}^2 - {f_2}^2}}{\phi _1} + \frac{{{f_1}^2 + {f_2}^2}}{{{f_1}^2 - {f_2}^2}}{\phi _2} \end{array}\right. $ | (1) |
式中,f1、f2为载波相位观测值的频率; ϕ1、ϕ2为载波相位观测值;Mp1、Mp2为一个历元的伪距多路径误差值。由式(1)知,多路径误差的值是由伪距观测值和载波相位观测值(包括整周模糊度)所决定的。通过逐历元处理伪距观测值和载波相位观测值,可以得到每个历元的多路径误差值,由于此时多路径误差值包含模糊度信息,因此求取一个完整弧段的多路径误差的均值,再分别用各个历元的多路径误差减去该均值,最终得到不包含模糊度信息的平滑后的MP值,多个历元的MP值组成了MP序列[7, 8]。
MP组合消除了卫地几何距离、电离层、对流层、钟差等因素的影响,仅受测量噪声和多路径误差的影响。对于GNSS不同系统中的MEO(medium earth orbit)卫星,以同一天的0点作为起点,取第一个弧段的观测数据,得到卫星的高度角和MP序列。图 1根据2015-03-01 JFNG测站的数据计算了GNSS 4个系统MEO卫星的MP序列与高度角的关系,测站接收机类型是Trimble Net R9接收机。可以看出,与GNSS其他卫星系统有别,北斗卫星导航系统MEO卫星的多路径序列(MP序列)中存在系统偏差,该系统偏差与高度角相关,其大小随着高度角的增大而减小。图 2进一步给出了北斗三类卫星的MP序列。事实上,除了GEO卫星的高度角变化不明显,无法看出该系统偏差的存在,IGSO(inclined geosynchronous satellite orbit)卫星的MP序列也存在与高度角相关的系统偏差。根据北斗IGSO卫星和MEO卫星与高度角的关系,考虑用多项式拟合的方法建立MP序列与高度角的多项式模型,达到根据高度角信息改正多路径系统偏差的目的。
 |
| 图 1 GNSS系统MEO卫星的多路径误差与高度角关系对比 Figure 1 Relationship Comparison of Multipath Deviation and Elevation for MEO Satellite of GNSS |
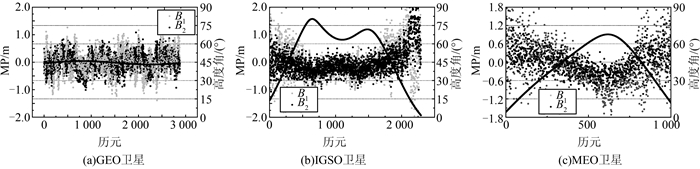 |
| 图 2 不同频率上的北斗卫星多路径误差序列与高度角序列 Figure 2 BDS MP Series and Elevation Series on Different Frequencies |
2 数据设置
实验中所有的数据都是由MGEX提供的,截至2015年,MGEX提供了全球大约70个可以接收北斗信号的GNSS接收机,大部分测站配备了可以接收北斗三频信号的Trimble Net R9接收机,少数测站的接收机只提供双频数据的Septentrio PolaRx4接收机。根据MEO卫星和IGSO卫星的星下点轨迹,选择15个测站2015年1-6月的观测数据(年积日1~180天),这些测站均使用Trimble Net R9接收机,数据采样率是30 s,在数据处理之前已对观测数据中的周跳进行了探测和修复。
本文选择用于建模的15个测站都可以收集MEO卫星所有高度角范围内的观测值数据,由于IGSO卫星的轨道是倾斜的,所以只有在东亚地区和澳大利亚才可以观察到较高高度角的北斗卫星观测数据,因此,实际15个测站仅有部分测站对模型建立有直接影响。考虑到MP组合观测值需要用到一种频率的伪距观测值和两种频率的载波相位观测值,针对北斗3种频率的数据可以有三种组合方式,本文仅对B1/B2频率下的观测值数据进行建模分析。
3 北斗卫星多路径系统偏差的改正基于北斗卫星伪距多路径系统偏差随着高度角的增大而减小的特性,建立北斗卫星多路径系统偏差与高度角的关系模型,采用多项式拟合的方法进行建模。一元多次多项式回归方程为:
| $ \hat y = {b_0} + {b_1}x + {b_2}{x^2} + \cdots + {b_m}{x^m} $ | (2) |
选择多项式拟合的方法是由于多项式回归可以处理非线性问题,当不清楚自变量和因变量的数学关系时,总可以用多项式回归进行分析,是回归分析中经常采用的拟合模型。
统计了北斗所有MEO卫星和IGSO卫星连续6个月的高度角信息和B1/B2频率上的伪距MP序列,通过程序实现拟合方法,分别得到每颗卫星(C06~C12和C14)B1/B2频率上的多项式参数b0、b1、b2,最后对所有IGSO、MEO卫星的参数求平均值,得到IGSO、MEO卫星B1/B2频率下的多路径系统偏差改正模型(表 1),IGSO卫星和MEO卫星B1/B2频率下的伪距改正值与高度角的关系如图 3所示。
| 表 1 基于多项式拟合的系统偏差改正模型 Table 1 Correction Model for Code Bias by Polynomial Fitting |
 |
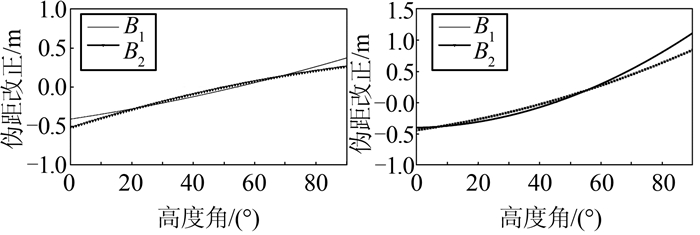 |
| 图 3 多项式模型下IGSO和MEO卫星伪距改正值 Figure 3 Pseudorange Correction of IGSO and MEO Satellites by Polynomial Model |
4 结果与分析
通过采用多项式拟合的方法对MP序列进行处理,得到北斗卫星多路径系统偏差的改正模型。为了验证改正模型的有效性,首先分析改正模型对MP序列系统偏差的改正效果,并进一步通过SPP定位精度检验经验公式的有效性。
4.1 MP序列改正结果由于原始的北斗MP序列观测值中包含了多路径系统偏差,比较改正前后MP组合观测值的特征以及MP组合观测值与高度角的关系,可以有效地验证伪距改正模型是否对多路径系统偏差进行了有效的改正。图 4给出了IGSO卫星改正前后的多路径误差与高度角的关系,可以看出,多路径系统偏差基本被消除,残余的多路径误差满足随机误差的特性。MEO卫星的改正效果与之一致。从图 4可以发现, 卫星高度角较低时,改正效果相对较弱,因为与其他时段比较,高度角较低时接收到卫星的数据有限,数据量的多少决定建模的稳定性。因此,低卫星高度角的改正效果相比其他卫星高度角时段要弱一些。
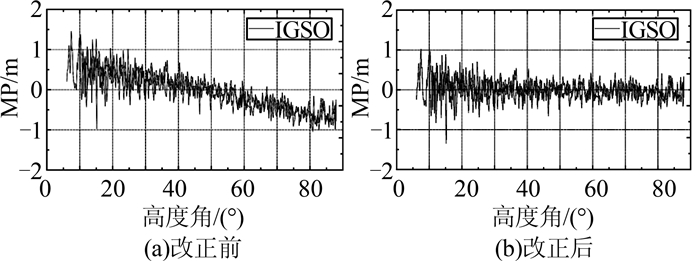 |
| 图 4 伪距多路径偏差改正前后MP组合观测值特征 Figure 4 MP Series Before and After Deviation Correction |
4.2 SPP定位效果
BDS精密单点定位是利用单台双频接收机的实测数据,结合精密的卫星轨道和卫星钟差产品对影响定位精度的各种误差进行模型改正或估计,得到接收机在地固坐标系中精确的位置和速度信息[9]。
本文选择了观测北斗卫星较多的CUT0、JFNG、GMSD、SIN1、NNOR、CUBJ、CUTB、CUTA、CUT2和CUT3共10个测站2015-05-02的数据,采用以下两种策略分别进行SPP处理:①不改正北斗卫星多路径系统偏差;②对北斗卫星的多路径系统偏差进行改正。然后分别计算伪距改正前后各个测站的定位精度, 并进行对比分析,定位精度通常根据E、N、U等3个方向坐标偏差的均方根值(root mean square, RMS)进行衡量[10-12]。对比分析结果如表 2所示。
| 表 2 SPP坐标偏差RMS对比分析/m Table 2 RMS Values Before and After Correction of SPP Result/m |
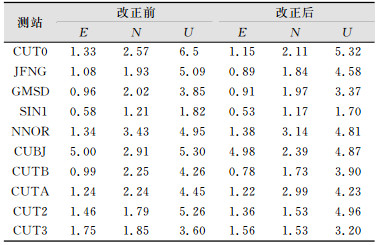 |
根据表 2给出的10个IGS站单天数据分析可知,改正伪距多路径可以使双频无电离层组合模型的SPP结果在E方向上平均提高0.1 m,N方向上平均提高0.28 m,U方向平均提高0.41 m,U方向上的提高最为明显。图 5给出了10个测站U方向上的精度比较。
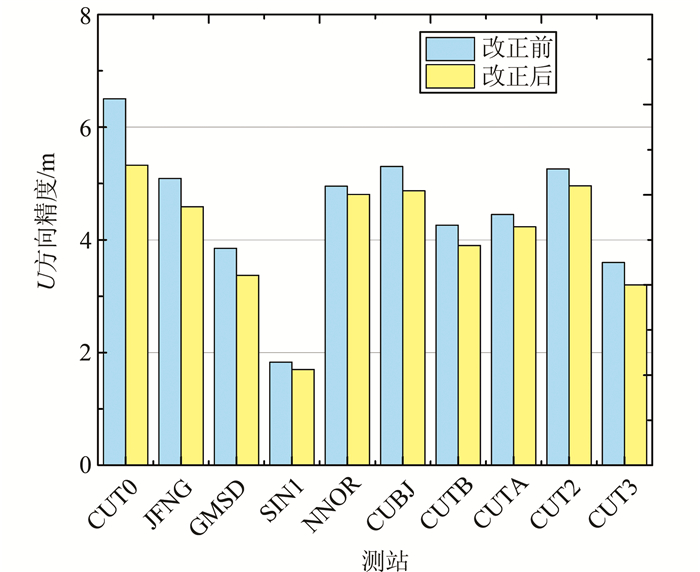 |
| 图 5 10个测站多路径系统偏差改正前后U方向的精度比较 Figure 5 Comparison of SPP's RMS in U Direction at 10 Stations |
5 结束语
对GNSS数据而言,多路径效应的影响与高度角有一定的关系,低高度角时,多路径误差的影响剧烈,随着高度角的增加,多路径效应的影响会有一种减弱的趋势,然而与GPS、GALILEO、GLONASS的多路径误差显著不同,随着高度角的减小,BDS的多路径误差数值有明显的近似线性的减小趋势,这是由于BDS的多路径误差中包含了卫星端多路径,根据此特征,本文选择2015年1~6月的数据建立了北斗MEO卫星和IGSO卫星在B1/B2频率上的伪距多路径偏差与高度角相关的多项式改正模型。
经过多项式模型改正后,北斗卫星多路径组合序列的系统误差基本得到消除,SPP的定位精度得到提升,E、N、U方向分别提高了0.1 m、0.28 m和0.41 m,其中U方向提升最大。由于GEO卫星的高度角变化较为稳定,难以确定多路径系统偏差与高度角的关系,因此针对GEO卫星多路径系统偏差的改正将是下一步研究的重点。
| [1] | Hauschild A, Montenbruck O, Sleewaegen J M, et al. Characterization of Compass M-1 Signals[J]. GPS Solutions, 2012, 16(1): 117–126 DOI: 10.1007/s10291-011-0210-3 |
| [2] | Perello G J V, Batzilis N, Risueño G L, et al. GNSS Payload and Signal Characterization Using a 3 m Dish Antenna[C]. ION GNSS 2012, Nashville, 2012 |
| [3] | Montenbruck O, Rizos C, Weber R, et al. Getting a Grip on Multi-GNSS-The International GNSS Service MGEX Campaign[J]. GPS World, 2013, 24(7): 44–49 |
| [4] | Zhang X H, Xiyang H E. BDS Triple-Frequency Carrier-Phase Linear Combination Models and Their Characteristics[J]. Science China: Earth Sciences, 2015, 58(6): 896–905 DOI: 10.1007/s11430-014-5027-9 |
| [5] | Wanninger L, Beer S. BeiDou Satellite-Induced Code Pseudorange Variations: Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639–648 DOI: 10.1007/s10291-014-0423-3 |
| [6] | 李征航. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010 |
| [7] | 张小红, 丁乐乐. 北斗二代观测值质量分析及随机模型精化[J]. 武汉大学学报·信息科学版, 2013, 38(7): 832–835 |
| [8] | Cazals F, Pouget M. Estimating Differential Quantities Using Polynomial Fitting of Osculating Jets[J]. Computer Aided Geometric Design, 2005, 22(2): 121–146 DOI: 10.1016/j.cagd.2004.09.004 |
| [9] | 侯超钧, 曾艳姗, 吴东庆, 等. 全局连续的分段最小二乘曲线拟合方法[J]. 重庆师范大学学报(自然科学版), 2011, 28(6): 44–48 |
| [10] | 王爱生, 欧吉坤. 无几何距离组合联合MW组合探测周跳的改进算法[J]. 数据采集与处理, 2007, 22(4): 468–474 |
| [11] | 潘树国, 王庆, 彭慧. 基于伪距宽巷组合的GPS模糊度固定方法[J]. 中国惯性技术学报, 2009, 16(6): 699–702 |
| [12] |
叶世榕. GPS非差相位精密单点定位理论与实现[D]. 武汉: 武汉大学, 2002 |
 2018, Vol. 43
2018, Vol. 43

