| 一种基于自学习的单像超分辨率方法 |
图像超分辨率概念最早由Tsai和Huang提出[1],之后引起众多学者的关注和研究,成为图像处理领域的研究热点之一。图像超分辨率是指由一幅低分辨率图像或图像序列恢复出高分辨率图像,从整体上可以分为两大类,即多幅图像超分辨率方法和单幅图像超分辨率方法。在高清数字电视、遥感应用、医学成像和安全监控等领域都具有十分重要的应用。
单幅图像超分辨率方法是指从单幅低分辨率的图像中恢复出由于图像获取时丢失的信息(主要是指高频信息)的过程。主要可以分为两类,一是没有训练样本的基于插值的单像超分辨率方法,二是有训练样本的基于学习的单像超分辨率方法。单像超分辨率方法最早由Goodman于20世纪60年代提出[2],其算法的主要思想是:对低分辨率图像采取规则插值。常见的规则插值方法有最邻近插值、双线性插值、双三次插值、样条插值等。在这类常见的规则插值方法中,未知像素的灰度值由其领域一定数目的像素值来估计计算,未考虑到图像自身的结构信息,容易造成边缘模糊。由于人类对图像中的边缘信息比较敏感,而边缘的清晰度往往与图像的整体质量息息相关,因此有关研究人员提出了基于边缘的插值算法。Li和Orchard提出了一种基于边缘导向的插值方法[3],通过低分辨率图像的局部协方差系数来估计高分辨率图像的协方差,达到修改高分辨率图像的结果。在基于边缘导向的插值方法的基础上,Andrea等提出了一种基于曲率的迭代插值算法[4]。基于插值的超分辨率方法简单易行,运算速度快,应用广泛。但是,低分辨率图像在下采样过程中,大量高频信息和细节丢失,在恢复高分辨率图像时,得到的高分辨率图像结果往往不太理想,图像质量差。基于学习的单像超分辨率问题是近年来的研究热点,通过机器学习方法从训练样本集中提取所需的高频信息,以达到提高图像分辨率的目的,大部分的基于学习的单像超分辨率方法都是基于图像分块的,将目标图像分割为多个子图像块,通过计算低分辨率图像块所对应的高分辨率图像块,得到高分辨率图像结果。与基于插值的单像超分辨率方法相比,基于学习的单像超分辨率方法速度相对较慢,需要大量的训练数据,可以较好地恢复图像的纹理信息[5-13]。然而,基于学习的单像超分辨率方法高度取决于训练集图像和原始低分辨率图像之间的一致性。
为了减少训练集中高频细节不兼容所带来的影响,本文提出了一种基于自学习的单像超分辨率方法。在基于图像自身相似性的基础上,不引入额外信息,充分发掘低分辨率图像本身的冗余性,建立图像重构模型,逐步提高原始低分辨率图像的分辨率,实现单幅图像的超分辨率。
1 基于自学习的单像超分辨率方法基于自学习的单像超分辨率方法的核心思想在于不引入额外信息,建立低分辨率图像与高分辨率图像之间的映射关系。由于自然图像中包含大量结构相似或相同的图像块,Glasner进行的图像相似性的验证实验[5]表明,不同尺度的图像中都能找到一定数量的原始图像块的相似子块,故原始低分辨率图像本身也可以提供很多有用的信息,这也是本文基于自学习的超分辨率方法的基础。
如图 1所示,在基于自学习的单像超分辨率方法中,给定原始低分辨率图像X、待重构高分辨率图像Y,设采样因子为s,经下采样再上采样得到较低分辨率图像Q,经上采样得到较高分辨率图像P。
 |
| 图 1 基于自学习的单像超分辨率方法 Figure 1 Single Image Super-Resolution Based on Self-Learning |
根据图像的自相似性原理,对于图像Q中的图像块(图 1(c)中的框),寻找图像P中的与其相似的图像块(图 1(d)中的框),计算图像Q中的图像块与图像P中与其相似的图像块两者之间的相似度和空间变换关系,建立两者之间的映射关系。同样,对于待重建高分辨率图像Y中的图像块(图 1(b)中的框),原始低分辨率图像X中一定存在与其相似的图像块(图 1(a)中的框)。因此,根据图像Q中的图像块与图像P中与其相似的图像块两者之间的映射关系,从而完成待重构高分辨率图像Y中的图像块的超分辨率重建,进而完成整个高分辨率图像的超分辨率重建。
将较高分辨率图像P的原始灰度图像分割成n像素×n像素大小的图像块,相邻图像块之间有一定的重叠度,则在较高分辨率图像P自身内存在着多个相似的图形子块,这些相似子块可以看做从同一高分辨率图像对应的低分辨率图像中获得。将由较高分辨率图像P分割的这些n像素×n像素大小的图像块作为较低分辨率测试数据集{Pk},k=1,2,…,K,其中K为低分辨率测试图像的分块总数。进行如下操作:
1) 将图像块Pk旋转,得到其旋转特征矢量集{Pki},i=0,1,2,3。其中,旋转特征矢量Pki由图像块Pk顺时针旋转90°×i,对应旋转矩阵为Hi,i=0,1,2,3。如图 2所示。
 |
| 图 2 图像块及其旋转特征矢量 Figure 2 Image Block and Its Rotation Characteristic Vector |
2) 在图像Q中遍历图像块,针对每一个图像块,计算该图像块与P中图像块Pk的旋转特征集{Pki}的欧氏距离,取最小值为该图像块的相似距离。寻找m个相似距离最小的图像块作为最相似的图像子块{Qkm},其对应的最小距离为min{Dkm}i,与图像块Pk的空间约束关系矩阵则为Hi-1。
3) 计算相似子块Qkm的重构权值ωkm,使重构误差最小,即
| $ {\varepsilon ^q} = {\left\| {\mathit{\boldsymbol{P}}_k^i - \sum \mathit{\boldsymbol{Q}}_k^m\cdot\omega _k^m} \right\|^2} = {\rm{min}} $ | (1) |
式中,Pki为图像子块{Qkm}对应满足最小相似距离的特征向量,并满足约束条件∑ωkm=1。
相似权重计算采用相似距离的负指数归一化,即
| $ \omega _k^m = \frac{{{{\rm{e}}^{ - {\rm{min}}{{\left\{ {D_k^m} \right\}}_i}}}}}{{\sum {{\rm{e}}^{ - {\rm{min}}{{\left\{ {D_k^m} \right\}}_i}}}}} $ | (2) |
4) 为了确定待重构高分辨率图像与原始低分辨率图像之间的映射关系,利用由较高分辨率图像P中图像块Pk与其相似的图像子块{Qkm}之间的映射关系,在原始低分辨率图像X中寻找与相似的图像子块{Qkm }一一对应的相似图像子块{Xkm},保持权值ωkm不变,重构待重建高分辨率图像Y中的图像块Yk为:
| $ {Y_k} = \sum \mathit{\boldsymbol{X}}_k^m\cdot\mathit{\boldsymbol{H}}_i^{ - 1}\cdot\omega _k^m $ | (3) |
5) 对每一个图像块Pk,根据这种基于自学习的单像超分辨率方法,得到对应重构待重建高分辨率图像Y中的图像块Yk,将这些图像块组成图像块数据集{Yk},并将这些图像块合并,则得到一幅比原始低分辨率图像分辨率高的高分辨率图像Y。
重复上述步骤1)~5),将重建的高分辨率图像Y作为低分辨率图像,再次重构高分辨率图像,每次放大s倍,放大循环次数n=lgS/lgs,其中S为最终放大次数,直至生成的高分辨率图像的分辨率满足所需要求。本文方法整体流程如图 3所示。
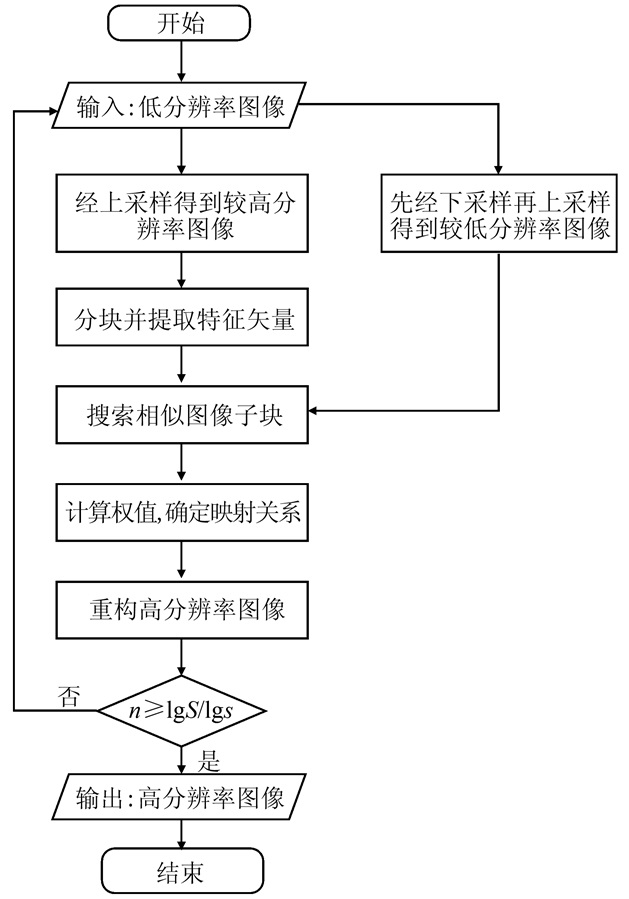 |
| 图 3 基于自学习的单像超分辨率方法流程图 Figure 3 Flow Chart of Single Image Super-Resolution Based on Self-Learning |
2 实验结果与分析
下面通过一系列实验验证文中基于自学习的单像超分辨率方法的有效性,并与最邻近插值法、双线性插值法以及双三次插值法进行比较,分别从超分辨率重建图像的视觉效果与真实高分辨率图像之间的均方差(mean squared error, MSE)、峰值信噪比(peak signl to noise ratios, PSNR)和结构相似性指标(structural similarity index method, SSIM)度量值来评价算法的性能。
在本实验中,较高分辨率图像P中的图像块大小为3像素×3像素,相邻图像之间重叠两个像素。在较低分辨率图像中寻找9个最相似的子图像块。本文基于自学习的单像超分辨率重建算法与其他几种方法的对比实验结果如图 4所示,各子图像右上角显示了图中实线框内区域的局部放大,以便更好地展示细节。
 |
| 图 4 不同方法的实验结果 Figure 4 Results of Different Methods |
从图 4可见,最邻近算法运算简单,运算量小,有明显马赛克现象;双线性插值具有低通滤波器的性质,图形轮廓模糊,细节退化;双三次插值法对影像的结构信息考虑较少,容易造成边缘模糊;本文提出的方法能恢复部分高频信息,得到较好的重建效果,边缘更锐利,纹理细节更丰富。
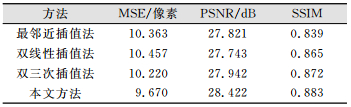
为定量地评估本文方法重建的高分辨率图像的质量,表 1给出了各种算法得到的高分辨率图像与真实高分辨率图像之间的MSE、PSNR、SSIM。可以看出,基于自学习的单像超分辨率方法优于其他算法。
| 表 1 不同方法重建图像质量比较 Table 1 Quality Comparison of Reconstruction Images by Different Methods |
 |
实验中图像块的大小对重建的高分辨率图像的性能有一定的影响,改变分割原始图像时的图像块大小,图像块大小分别为3像素×3像素、5像素×5像素、7像素×7像素、9像素×9像素、11像素×11像素,相邻图像之间重叠像素个数分别为2个、4个、6个、8个、10个,在较低分辨率图像中寻找9个最相似的子图像,实验结果如图 5所示。从图 5可见,随着图像块大小的增加,重建速度变快。当图像块较小时,重建的高分辨率图像质量变化不大;当图像块较大时,重建的高分辨率图像质量明显下降。产生这种现象的原因在于,当图像块的大小越大时,寻找到的与之相似的图像子块的相似度越差,因此,生成的高分辨率图像的质量也就越差。
 |
| 图 5 不同图像块大小的实验结果 Figure 5 Results of Different Image Blocks |
3 结束语
针对单幅图像的超分辨率重建,本文通过对原始低分辨率图像进行处理,得到较高分辨率的测试数据和较低分辨率的学习数据,在原始低分辨率图像中寻找测试数据中相似子区域的对应子区域,应用测试数据和学习数据间的映射关系,重建高分辨率图像,逐步提高原始低分辨率图像的分辨率。通过与最邻近插值法、双线性插值法以及双三次插值法进行比较,证实本文所提出的方法能有效提高原始低分辨率图像的分辨率,完成单幅图像的超分辨率。下一步工作将考虑图像块的大小,针对不同类型的图像,寻找合适的图像块大小对原始图像进行分割,在保证重建图像质量的同时,提高算法效率。
| [1] | Tsai R Y, Huang T S. Multiframe Image Restoration and Registration[C].Advances in Computer Vision and Image Processing, Greenwich, UK, 1984 |
| [2] | Goodman J W. Introduction to Fourier Optics[M]. New York: McGraw-Hill, 1968 |
| [3] | Li X, Orchard M T. New Edge-Directed Interpolation[J]. IEEE Transactions on Image Processing, 2001, 10(10): 1521–1527 DOI: 10.1109/83.951537 |
| [4] | Andrea G, Nicola A. Fast Artifacts-Free Image Interpolation[C]. Arquivos De Gastroenterologia, 2008, 47 (4):388-392 |
| [5] | Glasner D, Bagon S, Irani M. Super-Resolution from a Single Image[C]. IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 2009 |
| [6] | Zhang K, Gao X, Tao D, et al. Single Image Super-Resolution with Multiscale Similarity Learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(10): 1648–1659 DOI: 10.1109/TNNLS.2013.2262001 |
| [7] | Chang H, Yeung D Y, Xiong Y. Super-Resolution Through Neighbor Embedding[J]. Proceddings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004, (1): 275–282 |
| [8] | Roweis S T, Saul L K. Nonlinear Dimensionality Reduction by Locally Linear Embedding[J]. Science, 2000, 290(5500): 2323–2326 DOI: 10.1126/science.290.5500.2323 |
| [9] | Freeman W T, Jones T R, Pasztor E C. Example-Based Super-Resolution[J]. IEEE Computer Graphics and Applications, 2002, 22(2): 56–65 DOI: 10.1109/38.988747 |
| [10] | Sun J, Zheng N N, Tao H, et al. Image Hallucination with Primal Sketch Priors[C]. Proceddings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2003, 2(2):729-736 |
| [11] | 浦剑, 张军平, 黄华. 超分辨率算法研究综述[J]. 山东大学学报(工学版), 2009, 39(1): 27–32 |
| [12] | 苏衡, 周杰, 张志浩. 超分辨率图像重建方法综述[J]. 自动化学报, 2013, 39(8): 1202–1213 |
| [13] | 韩华, 王洪剑, 彭思龙. 基于局部结构相似性的单幅图像超分辨率算法[J]. 计算机辅助设计与图形学学报, 2005, 17(5): 941–947 |
 2017, Vol. 42
2017, Vol. 42

