| Galileo导航系统观测值的质量分析 |
2. 武汉大学导航定位技术研究中心,湖北 武汉,430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
Galileo导航系统是由欧洲设计并建造的全球卫星导航系统[1],截止2016年11月17日,在轨卫星总数已达到18颗。随着欧洲委员会在2016年12月15日正式宣布Galileo导航系统初始服务启动[2],GNSS正式进入4大系统融合的新时代,引起了国内外的广泛关注。
GNSS数据质量是影响导航定位性能和数据融合的关键因素,自然而然成为Galileo导航系统初始服务启动后人们关注的热点。因此有必要对Galileo系统观测值的数据质量进行分析。当前,对GPS和BDS的数据质量分析较多,主要体现在信噪比、多路径、残差等方面[3-9],而针对Galileo导航系统的观测数据质量分析较少。文献[10-13]针对早期Galileo导航系统的GIOVE-A和GIOVE-B试验卫星从信噪比、多路径、零基线和短基线残差等方面进行了分析,但两颗试验卫星已于2012年停止工作。文献[14]首次对IOV-1/2卫星E5信号的信噪比同GIOVE-A/B卫星进行了对比,表明在相同条件下,IOV卫星信噪比要高于GIOVE-A/B。文献[15-18]主要针对4颗Galileo IOV卫星从信噪比、多路径和双差残差等方面评估了其数据质量,结果表明Galileo E5信噪比最高,多路径最小。
在Galileo导航系统提供初始服务后,现已经能接收到至少13颗Galileo导航系统的观测值,这使得对现今Galileo导航系统观测数据进行较为系统全面的质量分析变得可行,而且十分必要。因此,本文采用了最新的GNSS观测数据,对所收集的Galileo导航系统观测值开展了多方面的质量分析,并与GPS和BDS的数据质量进行了对比分析,以期为Galileo导航系统的应用及其与其它系统的融合提供参考。
1 观测数据质量分析方案 1.1 信噪比信噪比是指信号功率PS与噪声功率PN的比值[19], 可以用来衡量测距信号质量的好坏:
| $ \mathrm{SNR}=\frac{P_{S}}{P_{N}} $ | (1) |
一般来说,信噪比越高,观测值的质量越好。在定位测量中,测量型GNSS接收机通常会记录信噪比数据,利用该数据能够较好地分析各卫星系统的各个频率上的信号质量。
1.2 伪距多路径利用伪距和相位观测值可以组成一种线性的无电离层和无几何距离组合,简称MP组合,它可以用来提取各频点的伪距多路径误差,其表达式为[20]:
| $ \mathrm{MP}_{j}=-\frac{f_{j}^{2}+f_{i}^{2}}{f_{j}^{2}-f_{i}^{2}} \lambda_{j} \varphi_{j}+\frac{2 f_{i}^{2}}{f_{j}^{2}-f_{i}^{2}} \lambda_{i} \varphi_{i}+P_{j}-B_{i j} $ | (2) |
式中, i和j (i ≠ j)代表不同频率;MPj为频率j上的多路径组合, 单位为m;λi和λi为不同频率载波波长;fi和fj代表不同频率;φi和φj为不同频率相位观测值;Pj为伪距观测值;Bij为包括模糊度项和硬件延迟项的组合,在无周跳的情况下认为是常数,通过多历元求平均得到MP序列均值,最后将MP序列减去该均值得到每个频率上的伪距多路径效应变化情况。
1.3 单差残差对于零基线,由于信号传播路径相同,采用站间单差可以消除卫星钟差、对流层延迟、电离层延迟以及多路径效应等误差[21]。零基线站间单差观测方程可以简写为:
| $ \Delta P_{r b}^{j}=\Delta o_{r b}^{j}+c \times \Delta \mathrm{d} t r+\Delta \varepsilon_{P}\\ \lambda \times \Delta \varphi_{r b}^{j}=\Delta \rho_{r b}^{i}+c \times \Delta \mathrm{d} t r+\lambda \Delta N_{r b}^{j}+\Delta \varepsilon_{\varphi} $ | (3) |
式中,上标和下标分别代表卫星和测站;Δ表示单差算子;P和φ分别为伪距观测值和载波相位观测值;ρ为卫星到测站间的几何距离;c为真空光速;dtr为接收机钟差;λ和N分别为载波相位的波长和整周模糊度;εP和εφ分别为伪距观测噪声和载波相位观测噪声。
载波相位单差模糊度可表示为:
| $ \Delta N_{r b}^{j}=\nabla \Delta N_{r b}^{i j}+\Delta N_{r b}^{i} $ | (4) |
式中,
| $ \Delta P_{r b}^{j}=\Delta o_{r b}^{j}+c \times \Delta \mathrm{d} t r+\Delta \varepsilon_{P}\\ \lambda \times \Delta \varphi_{r b}^{j}=\Delta \rho_{r b}^{j}+c \times \Delta \mathrm{d} t r+\lambda\left(\nabla \Delta N_{r b}^{i j}+\Delta N_{r b}^{i}\right)+\Delta \varepsilon_{\varphi} $ | (5) |
零基线中,双差模糊度
对于零基线,伪距单差残差ΔεP和载波单差残差Δεφ仅包含两台接收机的观测噪声。
假设零基线两端接收机的观测值精度相同,则根据误差传播定律可将单差观测值精度除以2,从而得到非差观测值的精度。
2 数据处理及结果分析 2.1 数据说明及卫星跟踪情况本文采用澳大利亚科廷大学CUT0和CUT2站初始服务启动前后的14 d的静态零基线观测数据分别对Galileo、GPS和BDS系统各频率的观测值进行信噪比、多路径和单差残差分析,在此过程中,GPS仅选择最新的12颗BLOCK IIF卫星进行分析。数据如下:接收机类型为Trimble NetR9;天线类型为Trimble 59800.00 SCIS;信号类型(括号内表示接收机通道)分别为GPS: L1(C)、L2(X)、L5(X);GAL: E1(X)、E5a(X)、E5b(X)、E5(X);BeiDou: B1I、B2I、B3I;采样间隔为30 s观测时间为2016年12月14日00:00:00~2016年12月27日23:59:30。CUT0站2016年12月14日当天内可跟踪的Galileo卫星颗数达到13颗,某一时刻跟踪的Galileo卫星多为4~6颗,能满足基本的定位要求。
2.2 信噪比分析图 1为Galileo导航系统、GPS和BDS各频率上的信噪比随高度角变化情况,可知,对于不同的卫星导航系统,各频率上的信噪比基本都是随高度角增大而增大,在卫星高度角较低时(10°以内),信噪比均在30 dB·HZ以上,在大于60°时,信噪比变化不明显,基本达到最大值。对于Galileo导航系统,E5信噪比最高,从40~58 dB·Hz,而E1、E5a、E5b信噪比基本一致,无明显区别,变化范围从36~52 dB·Hz。对于GPS,L5呈现最高信噪比,从40~57 dB·Hz,与Galileo E5几乎相同。GPS L1和L2频率上信噪比无明显差别,范围为33~52 dB·Hz,在20°高度角以内,低于Galileo E1、E5a和E5b,而高于20°时,与Galileo E1、E5a和E5b几乎相同。对于BDS,信噪比的变化范围为32~53 dB·Hz,B1I的信噪比在高度角小于55°时,基本低于B2I和B3I,而B3I的信噪比略高于B2I。在高度角小于60°时,BDS B1、B2、B3信噪比均低于Galileo E1、E5a、E5b和GPS L1、L2,在高度角高于60°时,基本相当,但仍低于Galileo E5和GPS L5。
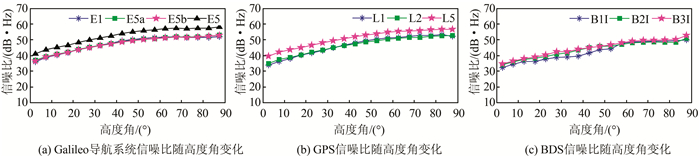 |
| 图 1 Galileo、GPS和BDS信噪比随高度角变化情况 Fig.1 SNR Changes with Elevation for Galileo System, GPS and BDS |
2.3 伪距多路径分析
图 2为Galileo导航系统、GPS和BDS各卫星各频率上的伪距多路径RMS。从图 2中可知,对于Galileo导航系统,不同卫星间差异不大,E1频点多路径最大,其次为E5b和E5a,而E5频点多路径最小。对于GPS,除个别卫星外,多路径大小基本L1频点最大,其次为L2频点,而L5频点多路径最小。对于BDS,B1I频点多路径最大,B3I频点多路径最小。
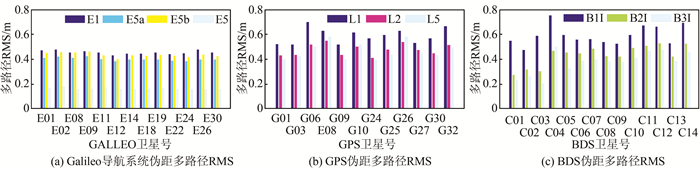 |
| 图 2 Galileo、GPS和BDS伪距多路径RMS Fig.2 RMS of Pseudorange Multipath for Galileo System, GPS and BDS |
统计Galileo导航系统、GPS和BDS所有卫星各个频率上的多路径RMS并求均值,结果见表 1,可见Galileo E5频点呈现最小多路径,而BDS B1I频点呈现最大多路径,Galileo导航系统4个频点多路径RMS值均小于GPS,而BDS B2I、B3I频点多路径小于GPS L2和L5频点。
| 表 1 Galileo, GPS和BDS伪距多路径RMS/m Tab.1 RMS of Pseudorange Multipath for Galileo System, GPS and BDS/m |
 |
为分析3个系统伪距多路径效应随高度角的关系,选取了E01、G10和C13、C14分别作为Galileo导航系统、GPS和BDS的代表。由于BDS GEO卫星高度角变化范围较小,一般在4°范围内变化,故图 3中未给出GEO卫星的情况, 而给出C13 (IGSO)和C14(MEO)的结果。
 |
| 图 3 E01、G10、C13和C14伪距多路径随高度角变化情况 Fig.3 Multipath Changes with Elevation for E01, G10, C13 and C14 |
从图 3可知,Galileo导航系统、GPS和BDS伪距多路径变化范围基本为±2 m,且随着高度角的增大而减小。在低高度角时,伪距多路径较大。同时,可以发现C14卫星伪距多路径不同于E01、G10和C13,其在高度角较高时存在一定的偏差,偏向负半轴,该偏差曾被Wanninger[22]等人发现并分析建模。
2.4 单差残差分析选取了Galileo E01、GPS G10分别作为代表来分析Galileo导航系统、GPS和BDS观测值单差残差结果,而对于BDS系统,由于BDS系统的卫星星座由GEO、IGSO和MEO 3种不同类型轨道卫星构成,便选取C01、C13和C14作为代表。
图 4(a)、图 4(b)分别为Galileo E01和GPS G10卫星单差相位残差和单差伪距残差时序图,可知E01和G10单差相位残差大多在±4 mm内,E01、G10单差伪距残差基本在±0.3 m和±0.5 m内,且E01的4个频率单差相位残差和单差伪距残差随高度角变化不明显,G10单差伪距残差在低高度角时较大。
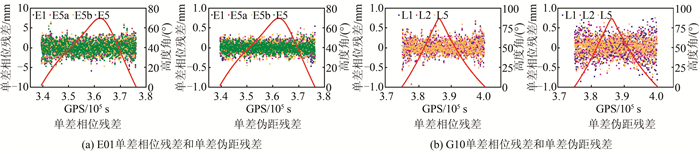 |
| 图 4 E01和G10单差相位残差和单差伪距残差 Fig.4 Single Difference Phase Residual and Code Residual for E01 and G10 |
图 5为BDS C01、C13和C14卫星单差相位残差和单差伪距残差时序图,从图中可知,C01卫星高度角变化范围为3°,其单差相位残差和单差伪距残差分布较均匀,分别在±5 mm和±0.5 m内变化。C13和C14卫星在低高度角时均呈现较大的残差,且可以看出单差伪距残差B1频点相对较大。
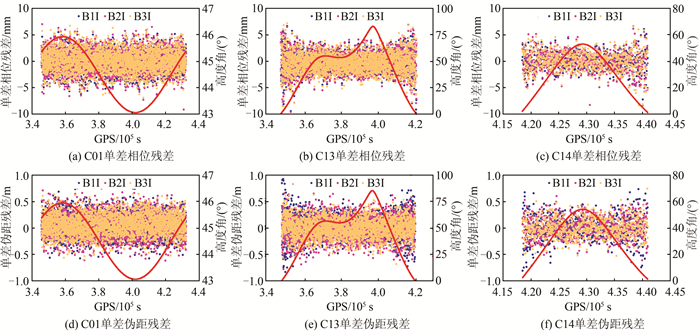 |
| 图 5 C01、C13和C14单差相位残差和单差伪距残差 Fig.5 Single Difference Phase Residual and Code Residual for C01, C13 and C14 |
表 2统计了Galileo、GPS和BDS系统的非差相位观测值和非差伪距观测值的精度。对于BDS系统,分GEO、IGSO和MEO 3种轨道卫星分别统计,表中数值为多颗卫星的均值。从表 2可知,对于Galileo系统,相位观测值精度E1最高,而E5a、E5b和E5相当,而伪距观测值精度E5最高,E5b最差。对于GPS系统,相位观测值精度与Galileo基本相当,而伪距观测值精度明显较Galileo导航系统差,其中L1伪距精度最差,L5伪距精度最高。对于BDS系统,GEO、IGSO和MEO观测值精度有所差异,其中观测值精度IGSO最高,其次为MEO卫星,而GEO卫星最差。Galileo导航系统、GPS和BDS 3系统对比分析可知,BDS相位观测值精度最差,而伪距观测值精度优于GPS,但较Galileo导航系统差。
| 表 2 Galileo、GPS和BDS零基线非差相位和非差伪距观测值精度/mm Tab.2 Precision of Un-differenced Phase and Code Observations of Zero Baseline for Galileo, GPS and BDS/mm |
 |
2.5 单点定位结果分析
为了评估Galileo伪距观测值的基本定位性能,利用武汉大学测绘学院研制的高精度GNSS动态定位测速与定姿软件KinPOS分别计算Galileo、GPS、BDS、Galileo/GPS、Galileo/BDS和Galileo/GPS/BDS组合系统的单点定位结果,并将计算结果与参考真值作差后转换到测站坐标东(E)、北(N)、上(U)3个方向。所用的数据为澳大利亚Curtin大学CUT0站2016-12-14至2016-12-27共14 d的观测数据,单点定位时采用单频观测值和广播星历,电离层和对流层均采用模型改正,卫星截止高度角为10°。
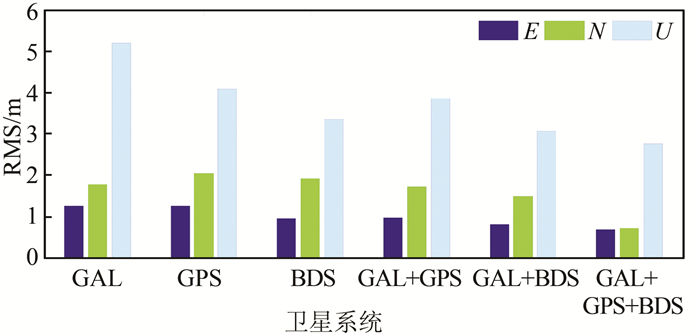
图 6为单系统和组合系统单点定位误差在E、N、U方向的RMS统计情况,可知,无论是单系统还是组合系统,单点定位E方向的误差最小,而U方向最大。对于Galileo导航系统,E、N、U 3个方向位置误差RMS分别为1.268 m、1.790 m、5.200 m;与GPS和BDS单点定位结果对比可知,Galileo导航系统单点定位U方向误差较GPS和BDS大,但E方向和N方向3系统差异不大。Galileo/GPS、Galileo/BDS组合系统单点定位结果较单系统在E、N、U 3个方向上定位精度均有所提高,而Galileo/GPS/BDS 3系统组合单点定位精度最高,这是由于卫星数较多且分布更均匀,PDOP值得到了显著的改善。
 |
| 图 6 不同GNSS系统的单点定位位置误差RMS统计 Fig.6 RMS of the SPP Position Errors for Different GNSS System |
3 结束语
本文主要从观测值的信噪比、伪距多路径效应、单差残差和非差观测值精度等方面深入分析了Galileo导航系统初始服务初期的观测数据质量,同时与GPS和BDS系统的观测数据质量进行了对比,最后给出了Galileo导航系统以及组合系统单点定位精度。
1) Galileo导航系统各频率上的信噪比均呈现出随高度角增大而增大的趋势,其中E5信噪比最高,E1、E5a和E5b次之且基本相当。整体而言,Galileo的信噪比最高,其次为GPS,而BDS信噪比最低。
2) Galileo导航系统各频率上的伪距多路径均呈现出随高度角增大而减小的趋势,其中E1频点伪距多路径最大,其次为E5b和E5a, 而E5最小;Galileo导航系统4个频率上的伪距多路径均小于GPS L1、L2和L5以及BDS B1I频率上的伪距多路径。
3) Galileo导航系统各频率上单差相位残差均在±4 mm内,单差伪距残差均在±0.3 m内。
4) Galileo导航系统相位观测值精度E1最高,E5a、E5b和E5次之且基本相当;而伪距观测值精度E5最高,E5b最差;Galileo导航系统相位观测值和伪距观测值精度均优于GPS和BDS的相位和伪距观测值精度。
5) Galileo导航系统水平精度约为2.2 m,与GPS和BDS的水平精度差异不大,而高程精度约为5.2 m,与GPS和BDS有一定的差距;Galileo/GPS、Galileo/BDS组合系统单点定位精度较单系统在E、N、U 3个方向上均有所提高,而Galileo/GPS/BDS组合定位精度最高。
| [1] |
EU. European GNSS (Galileo) Open Service Signal in Space Interface Control Document (OS-SIS-ICD)[R]. European Union, Issue 1.3, Brussel, The Kingdom of Belgium, 2016
|
| [2] |
EU. European GNSS (Galileo) Initial Services Open Service Service Definition Document (OS-SDD) [R]. European Union, Issue 1.0, Brussel, The Kingdom of Belgium, 2016
|
| [3] |
范士杰, 郭际明, 彭秀英. TEQC在GPS数据预处理中的应用与分析[J]. 测绘信息与工程, 2004, 29(2): 33-35. DOI:10.3969/j.issn.1007-3817.2004.02.014 |
| [4] |
张小红, 丁乐乐. 北斗二代观测值质量分析及随机模型精化[J]. 武汉大学学报·信息科学版, 2013, 38(7): 832-836. |
| [5] |
潘林, 蔡昌盛, 戴吾蛟, 等. 北斗与GPS数据质量对比分析[J]. 全球定位系统, 2013, 38(2): 23-26. DOI:10.3969/j.issn.1008-9268.2013.02.005 |
| [6] |
白征东, 吴刚祥, 任常. 北斗观测数据的质量检查与分析[J]. 测绘通报, 2014(6): 10-13. |
| [7] |
范晓燕, 周乾. TEQC在GPS数据分析及多路径效应中的应用研究[J]. 测绘信息与工程, 2011, 36(3): 16-19. |
| [8] |
Shi C, Zhao Q, Hu Z, et al. Precise Relative Positioning Using Real Tracking Data from COMPASS GEO and IGSO Satellites[J]. GPS Solutions, 2013, 17(1): 103-119. DOI:10.1007/s10291-012-0264-x |
| [9] |
Yang Y, Li J, Wang A, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China:Earth Sciences, 2014, 57(1): 144-152. DOI:10.1007/s11430-013-4769-0 |
| [10] |
Simsky A, Mertens D, Sleewaegen J M, et al. Experimental Results for the Multipath Performance of Galileo Signals Transmitted by GIOVE-A Satellite[J]. International Journal of Navigation & Observation, 2008. DOI:10.1155/2008/416380 |
| [11] |
Simsky A, Mertens D, Sleewaegen J M, et al. Multipath and Tracking Performance of Galileo Ranging Signals Transmitted by GIOVE-B[C].ION GNSS'08, Savannah, USA, 2008
|
| [12] |
Montenbruck O, Hauschild A, Hessels U. Characterization of GPS/GIOVE Sensor Stations in the CONGO Network[J]. GPS Solutions, 2011, 15(3): 193-205. DOI:10.1007/s10291-010-0182-8 |
| [13] |
Bakker P F D, Tiberius C C J M, Marel H V D, et al. Short and Zero Baseline Analysis of GPS L1 C/A, L5Q, GIOVE E1B, and E5aQ Signals[J]. GPS Solutions, 2012, 16(1): 53-64. DOI:10.1007/s10291-011-0202-3 |
| [14] |
Margaria D, Fantino M, Musumeci L. Acquisition and Tracking of Galileo IOV E5 Signals: Experimental Results and Performance Evaluation[J]. Annual of Navigation, 2012, 19(1): 105-120. DOI:10.2478/v10367-012-0009-5 |
| [15] |
Cai C, Luo X, Xiao Z L Q. Galileo Signal and Positioning Performance Analysis Based on Four IOV Satellites[J]. Journal of Navigation, 2014, 67(5): 810-824. DOI:10.1017/S037346331400023X |
| [16] |
Cai C, He C, Santerre R, et al. A Comparative Analysis of Measurement Noise and Multipath for Four Constellations: GPS, BeiDou, GLONASS and Galileo[J]. Empire Survey Review, 2015, 48(349): 287-295. |
| [17] |
Quan Y, Lau L, Roberts G W, et al. Measurement Signal Quality Assessment on all Available and New Signals of Multi-GNSS (GPS, GLONASS, Galileo, BDS, and QZSS) with Real Data[J]. Journal of Navigation, 2015, 69(2): 313-334. |
| [18] |
Nadarajah N, Khodabandeh A, Teunissen P J G. Assessing the IRNSS L5-Signal in Combination with GPS, Galileo, and QZSS L5/E5a-Signals for Positioning and Navigation[J]. GPS Solutions, 2016, 20(2): 289-297. DOI:10.1007/s10291-015-0450-8 |
| [19] |
Hranac R, Currivan B. Digital Transmission: Carrier-to-Noise Ratio, Signal-to-Noise Ratio, and Modulation Error Ratio[R]. White Paper, Broadcom Corporation and Cisco Systems, Inc, San Diego, USA, 2006
|
| [20] |
Estey L H, Meertens C M. TEQC: The Multi-Purpose Toolkit for GPS/GLONASS Data[J]. GPS Solutions, 1999, 3(1): 42-49. DOI:10.1007/PL00012778 |
| [21] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉大学出版社: 武汉, 2010.
|
| [22] |
Wanninger L, Beer S. BeiDou Satellite-Induced Code Pseudorange Variations: Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639-648. DOI:10.1007/s10291-014-0423-3 |
 2019, Vol. 44
2019, Vol. 44


