| 一种空间面数据宽窄特征判断方法 |
面状数据是地理目标中的重要几何类型,其千奇百态的形状在面状数据处理上有着重要的作用[1]。为了剖析面状数据的边界、结点等结构,许多学者在面状数据上建立了Delaunay三角网,进行了如面状数据的化简[2]与合并[3]、Voronoi图建立[4]、道路[5]或河网[6]中心线提取、注记自动配置[7]等研究。Delaunay三角网[8]的基本算法有逐点插入法、生长法、分治法,很多学者对其进行了优化[9-17]。其中,约束Delaunay三角网[18]是一种针对线状或面状目标(面状数据),防止三角网的边穿越线状或面状目标而加入一些相关限制条件来建网的方法。在地理信息系统、地学分析、计算机图形等领域,无论是二维平面还是三维角度,Delaunay三角网都是一种不可或缺的分析手段。因此,本文用其进行面状数据宽窄特征的分析及判断。
面状数据的宽窄判断是模拟人类对形状的认知规律的一个例子,在判断过程中多依赖于人眼对面状数据的形状特征的视觉感知模式。不同于现有面状数据形状分析方法[19],本文不对面状数据的宽窄特征进行定量描述,而是从面状数据的数据特征出发,从全局到局部提出了面状数据宽窄特征的判断方法,保留宽面部分,以便改善后续的制图视觉效果以及进行结构分析,并通过可视化分析实验对该方法的有效性进行检验。
1 面状数据宽窄特征判断方法面状数据常存在一些因为生产质量或者本身具有的狭小细节,在一定可忽略条件下,可视这些细节为可省略的部分。针对如何判断面状数据的宽窄部分,本文提出一种空间面数据宽窄特征判断方法,包括全局式宽窄特征判断和局部式宽窄特征判断两部分。首先整体判断面状数据的面积是否符合狭窄面特征;然后利用最小外接矩形进一步分析面状数据的形状;最后利用Delaunay三角网分析原始面数据内部的宽窄细节,得到面状数据的宽窄形状特征判断结果。
1.1 全局式宽窄特征判断1)面积直接判定。设定宽度阈值σ,将面积小于σ2的面状数据直接判断为狭窄面。即如果其本身具有狭小的特征,直接判断为狭窄面状数据。
2)利用最小外接矩形判定。对于面状数据目标而言,用其外接矩形来近似描述其形状是地理信息系统和图形学领域的一种常用方法。
如果其最小外接矩形面积和其本身面积相差较大,则以面积比率ε(取值0. 85)衡量,大于该比率,则继续比较面状数据的长宽值之和(如果面状数据有内边界或洞,长宽值包括内边界的长宽)的一半与最小外接矩形宽度的比例,大于宽度阈值σ的则认定为宽面,反之认为该面状数据是狭窄面状数据;若小于等于ε,则直接认定其为狭窄面状数据。
3)判断窄小三角形占比。在无法通过面状数据本身初步判断宽窄特征时,对面状数据建立约束Delaunay三角网,按式(1)三角形宽窄特征式与邻接关系聚类所有窄小三角形和宽三角形。
| $ {T_{{\rm{shape }}}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{ 窄, }}\exists {L_S} > \alpha \times \sigma }\\ {{\rm{ 宽, }}\forall {L_S} \le \alpha \times \sigma } \end{array}} \right. $ | (1) |
式中,LS为三角形的边长;α为权重,取值为1. 13,可根据实际情况设置不同的值,权重值越大,面状数据窄小性质的判断程度越低,得到的窄小三角形个数相应较少。若三角形的3个边的边长都在α权重的宽度阈值σ范围内,则为宽三角形;其余情况下则为窄三角形。如果三角网中的窄小三角形在三角网中占了较大比例,则直接判断该面状数据为狭窄面状数据。该比例设定为0. 9,值越小,越容易将面状数据划定为狭窄面状数据。
1.2 局部式宽窄特征判断若无法从全局的角度对面状数据的宽窄特征进行判断,则基于第3种全局式宽窄定性方法得到的宽窄三角形聚类结果,对所有三角形进行分类处理。
根据面状数据三角网内的宽窄三角形聚类情况,从局部的角度对宽窄三角形进行调整,并对各类调整情况进行了分类描述以及调整方法的介绍,具体如下:
1)单独宽或窄三角形成类的调整。宽窄三角形特征聚类时,可能出现对应的三角形周围无邻接且同特征的三角形的情况,导致其被单独划分为一类。
① 独立宽三角形成类。单个宽三角自成一类时,直接将该宽三角形合并至左右邻接的窄小三角形中,并重新根据式(1)聚类此处的窄小三角形。
② 单个窄三角形成类。根据窄小三角形的角度和边长特征,以窄小三角形某内角大于一定阈值的拐点以及该内角相对边大于一定长度为条件来进行调整。具体方法如图 1所示,如果与该独立窄小三角形与宽三角形的公共边se首尾点关联的三角形外边界(如sa、ss'和ea、ee')两边界不平行,形成的外角大于一定拐角阈值λ,则认为对应的公共边首尾点是拐点。只要存在一个拐点(s或e),就能获取窄小三角形中该拐点相对边(ae或as),计算拐点相对边长与公共边长的比例,如果不小于一定边长比例阈值δ,则认定独立三角形相对邻接的宽三角形过于狭窄,不调整此处的窄小三角形。
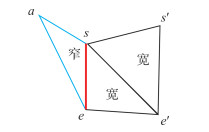 |
| 图 1 单独窄三角形的调整模式 Fig.1 Adjustment Mode of a Single Narrow Triangle |
2)“细颈”部分的窄小三角形判断。若某类窄小三角形呈现狭长形状且面积非常小,则以此类窄小三角形的骨架线长度与平均宽度的比例判断狭长性质,大于长宽比阈值κ的认定其狭长,表现为“细颈”特征,如图 2所示,这类窄小三角形不再参与调整。
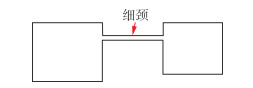 |
| 图 2 “细颈”特征 Fig.2 Characteristic of"Thin Neck" |
平均宽度计算公式如下:
| $ {M_A} = \frac{{\sum\limits_{i = 0}^n {{L_i}} {A_i}}}{{\sum\limits_{i = 0}^n {{A_i}} }} $ | (2) |
式中,Ai表示三角形的面积;Li表示“细颈”中每个三角形的长度,该长度根据图 3所示的三角形类型获取,Ⅰ类三角形的长度为次长边相对点的垂距,Ⅱ类三角形的长度为非公共边相对点的垂距,Ⅲ类三角形的长度为三条边上对应的最长垂距。
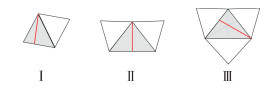 |
| 图 3 三角形宽度 Fig.3 Width of Triangles |
面积判断方法如下:窄小三角形的总面积小于预设权重倍数下的三角网总面积,则权重设为0. 05。
3)末端窄小三角形处理。当少于指定数量的窄小三角形聚类且邻接的宽三角形只有一类时,这类三角形为末端窄小三角形。本文指定个数限制为5个。
如果末端窄小三角形无狭长末端,则将其归并为宽面三角形。判断狭长末端的方法如下:如果该分类下的Ⅰ类三角形的边界长度差异小(如图 4中Ⅰ类三角形的边界s1 e1和s2 e1),以及Ⅱ类三角形的边界和Ⅰ类三角形的较长边界不平行(如图 4中较长边s1e1和Ⅱ类边界s2e2),则认定该处不是狭长末端;如果该分类下的Ⅰ类三角形的边界长度差异大,则认定该处为狭长末端,其中差异上限设定为2倍,此处的边界指面状数据部分轮廓。
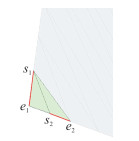 |
| 图 4 末端窄小三角形处理 Fig.4 Process of a Narrow Triangle at the End |
4)末端宽三角形调整。当与宽三角形邻接的窄小三角形只有一类时,这类宽三角形为末端宽三角形。若末端宽三角形的平均宽度与邻接的窄小三角形平均宽度之比不大于2,则将其归并为窄小三角形。
5)窄小“细颈”调整。如果某处具有“细颈”特征,但其骨架线长度小于一定阈值,且该长度与其平均宽度的比例不超过长宽比阈值κ,则需要调整该处的窄小“细颈”。
如果这类窄小三角形的平均宽度大于预设权重倍数下的分割宽度阈值σ,权重设为0. 85,直接将其归属为宽三角形。不大于该阈值时,与邻接的宽三角形的平均宽度的比例只要存在不大于1. 5的情况,且窄小三角形个数比邻接的宽三角形个数少,则将该处窄小三角形调整为宽三角形,并与邻接的宽三角形合并成一类。
6)末端窄小三角形调整。末端窄小三角形个数比邻接的宽三角形数量少时,若末端窄小三角形的骨架线长度与平均宽度的比例不大于末梢窄面保留的长宽比阈值ρ,且邻接的宽三角形平均宽度与末端窄小三角形的平均宽度的比例小于等于2,则将其归并为宽三角形;若宽度比例大于2,无狭长末端的该类窄小三角形骨架线长度小于阈值ω时,则将其转化为宽三角形。
7)末端小窄面再调整。如果窄小三角形与宽三角形的邻接边的边长在分割宽度阈值σ内,邻接边中点与末端窄小三角形中Ⅰ类三角形的边界点的距离的最大值小于σ,且小于邻接边长,或者邻接边与最大距离的比例大于1. 2,则这类窄小三角形被定义为小窄面,直接将其并入邻接的宽三角形。
2 实验与分析 2.1 实验数据与环境为检验本文方法的有效性,依托中国测绘科学研究院研制的WJ-Ⅲ地图工作站,嵌入一种基于Delaunay三角网的面状数据宽窄判断方法,在C++环境下运行算法。实验数据取自贵州省某区域图斑数据,该区域的面状数据细节特征具有代表性,涵盖了以上提出的多种局部调整场景,系统运行环境为Windows 7 64位操作系统,中央处理器(central processing unit,CPU)为Intel Core I7-4790,单机8核8线程,主频3. 6 GHz,内存8 GB,固态硬盘1 024 GB。实验中使用了3块不同的面状数据进行宽窄特征判断,其面积分别为1 357.35 km2、1 204.28 km2和1 049.50 km2。方法中所涉及的阈值中,分割宽度阈值σ设为30 m,拐点判断阈值λ设为π/9,长宽比阈值κ设为50,末梢窄面长度较短时转化为宽面的阈值ω设为60 m,末梢窄面保留的长宽比阈值ρ设为3。预设阈值根据实验区域特征调整,具体受经验、人眼视觉、制图要求等影响。
2.2 可视化实验分析图 5展示了实验数据局部的宽窄分割结果。在全局角度上,利用本文方法能从实验区域图斑成功判断出狭窄面状数据;在局部角度上,利用本文方法能成功分割出狭窄细节,包括“细颈”、狭长末端和处于图斑之间的其他狭窄细节。表 1展示了宽窄面的判断结果,3个实验区域分别有28、22、34个窄面,分别占原始面个数的43. 08%、32. 84%、30. 63%。这些细节是各种各样图斑中常见的呈窄小、尖角特征的面要素,常处于面状数据末梢或周围。在一定条件下,这类细节通常是制图综合任务中需要化简的面状数据细节,对该类图斑细节进行判断并删除后,更便于对图斑结构进行剖析,在制图任务中得到更好的制图效果或分析结果。
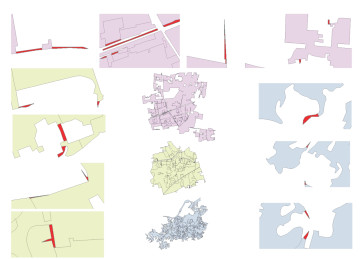 |
| 图 5 宽窄判断结果 Fig.5 Results of the Width and Narrowness Identification |
| 表 1 宽窄面个数统计 Tab.1 Statistics of the Numbers of Wide and Narrow Polygons |
 |
在统计结果中会出现宽面个数大于原始面个数的情况,其原因是在局部式的宽窄特征判断过程中,会分割出多个原始面内部的较宽部分,最终重构成多个宽面。
3 结束语本文通过分析面状数据的形状特征,设计了3种宽窄面判定方法,从全局角度判断面状数据的宽窄特征,再从局部角度利用Delaunay三角网,通过7种模式进行面状数据细节调整,得到宽和窄两种面状数据分割细节,进而得到面状数据的宽窄特征判断结果。实验结果表明,该方法适用于面状数据去尖端、去狭长等空间面数据处理场景或地图制图、图形分析等应用场景。需要指出的是,算法受多项人工指定的参数限制,主要是受不同的面状数据宽窄判断场景影响,会有不同人眼主观阈值,如何自适应判断面状数据的宽窄是值得研究的方向。
| [1] |
艾廷华, 郭仁忠, 陈晓东. Delaunay三角网支持下的多边形化简与合并[J]. 中国图象图形学报, 2001, 6(7): 703-709. DOI:10.3969/j.issn.1006-8961.2001.07.017 |
| [2] |
郭仁忠, 艾廷华. 制图综合中建筑物多边形的合并与化简[J]. 武汉测绘科技大学学报, 2000, 25(1): 25-30. |
| [3] |
黄继风. 基于Delaunay三角网的城市多边形合并算法[J]. 计算机工程与设计, 2004, 25(7): 1 220-1 222. DOI:10.16208/j.issn1000-7024.2004.07.060 |
| [4] |
艾廷华. Delaunay三角网支持下的空间场表达[J]. 测绘学报, 2006, 35(1): 71-76. DOI:10.3321/j.issn:1001-1595.2006.01.014 |
| [5] |
艾廷华, 郭仁忠. 基于约束Delaunay结构的街道中轴线提取及网络模型建立[J]. 测绘学报, 2000, 29(4): 348-354. DOI:10.3321/j.issn:1001-1595.2000.04.012 |
| [6] |
张立锋, 程钢, 白鸿起. 基于Delaunay三角网的河流中线提取方法[J]. 测绘与空间地理信息, 2006, 29(4): 80-82. DOI:10.3969/j.issn.1672-5867.2006.04.024 |
| [7] |
余代俊, 耿留勇, 兰燕. Delaunay三角形法实现面状要素自动注记初探[J]. 测绘科学, 2007, 32(4): 81-82. |
| [8] |
邵春丽, 胡鹏, 黄承义, 等. Delaunay三角网的算法详述及其应用发展前景[J]. 测绘科学, 2004, 29(6): 68-71. |
| [9] |
贺全兵, 黎贵友, 文进, 等. 生成Delaunay三角网的改进算法[J]. 计算机与数字工程, 2006, 34(5): 50-52. |
| [10] |
汤泉, 牛铮. 构建Delaunay三角网的改进算法[J]. 计算机应用, 2007, 27(S1): 158-159. |
| [11] |
高莉. 改进的Delaunay三角剖分算法研究[D]. 兰州: 兰州交通大学, 2015
|
| [12] |
徐道柱, 刘海砚. 大量约束边条件下Delaunay三角网的快速生成[J]. 测绘工程, 2007, 16(3): 6-10. |
| [13] |
郭兆胜, 张登荣. 一种改进的高效Delaunay三角网的生成算法[J]. 遥感信息, 2005, 20(1): 15-17. |
| [14] |
何俊, 戴浩, 谢永强, 等. 一种改进的快速Delaunay三角剖分算法[J]. 系统仿真学报, 2006, 18(11): 3 055-3 057. |
| [15] |
余代俊, 蒲朝旭, 朱逍贤. 一种Delaunay三角剖分的改进算法[J]. 测绘通报, 2014(6): 51-54. |
| [16] |
周婷, 彭正洪, 密新武. Delaunay三角网生长算法改进与实现[J]. 图学学报, 2013, 34(5): 12-15. |
| [17] |
青文星, 陈伟. Delaunay三角网生成的改进算法[J]. 计算机科学, 2019, 46(S1): 226-229. |
| [18] |
毛建华, 郭庆胜, 闫浩文, 等. 限制性Delaunay三角网的剖分算法[J]. 兰州铁道学院学报, 2002, 21(3): 73-75. |
| [19] |
刘鹏程. 形状识别在地图综合中的应用研究[D]. 武汉: 武汉大学, 2009
|
 2023, Vol. 48
2023, Vol. 48


