| 宝兰高铁某标段CPI复测数据处理与稳定性分析 |
2. 兰州交通大学测绘与地理信息学院,甘肃 兰州,730070
2. School of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China
高速铁路对于精度的要求极高,因此它的测量方法也跟普通铁路有所不同,控制网复测过程中要有完整、高效而且严密的测量系统和数据处理方法[1-4],这就需要有高精度的测量设备及技术来支持[5]。近年来,使用较为普遍的是GPS技术,其方便使用、测站之间无需通视、全天候作业、平面测量精度高等特点,成为了高速铁路平面控制网测量的最佳方法[6-8]。CPI平面控制网复测是在原测基础上进行复测检查,为判断CPI网点是否发生变化提供依据,通过检查来确保CPI控制网的精度达到足够高的要求,为后期逐级加密的控制网提供高精度基准来控制高速铁路的建设,使高速铁路达到规范要求,确保轨道的平顺性以及列车高速运行过程中的舒适性和安全性。
1 复测技术方案 1.1 CPI复测作业方法及精度指标CPI控制网测量主要采用二等GPS测量,采用边联式进行构网,由三角形或者大地四边形构成带状网形,外业观测换站时,要始终保证有一条边不动,采用边联式进行推进测量。具体网形如图 1所示。
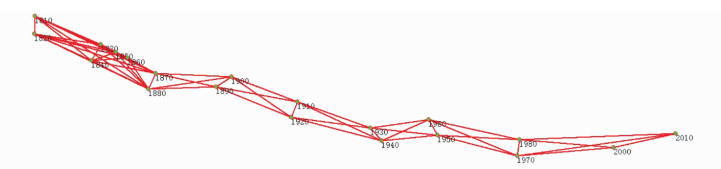 |
| 图 1 CPI测量网形示意图 Fig.1 Diagram of CPI Measurement Network |
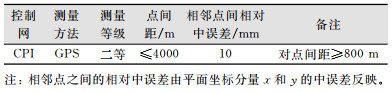
| 表 1 高速铁路CPI控制网复测等级要求 Tab.1 Requirements for Retest Level of CPI Control Network of High Speed Railway |
 |
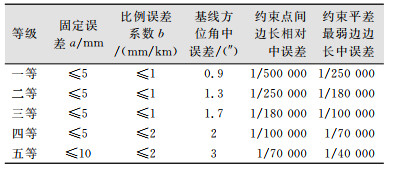
| 表 2 GPS控制网测量(复测)精度要求 Tab.2 Accuracy Requirement of GPS Control Network Survey (Retest) |
 |
1.2 控制网现状
在复测开始之前对精测网控制桩现状进行了调查,见表 3。
| 表 3 控制网现状调查表 Tab.3 Questionnaire on Current Situation of Control Network |
 |
由表 3可知,CPI控制点没有被破坏,故可以直接应用于CPI控制网的复测。明确相关作业规定、网形设计原则以及CPI控制点布设方法后,可根据实际情况对组织人员原测网形进行复测,安排外业人员进行外业数据采集,CPI控制网复测时需要联测邻近标段的控制点。
2 基线向量解算 2.1 基线向量解算时应遵守的规则1) 基线向量解算时,卫星星历统一采用广播星历,卫星高度截止角采用20°;
2) 同一时段观测值的数据剔除率不得大于10%,否则需要重新测量;
3) 任一时段同步观测时间,CPI复测网不得小于90 min,任一时段有效卫星数不得少于4颗;
4) 基线向量满足验收标准后,按最小闭合环原则对全网的基线向量进行闭合环搜索,并且对闭合环的闭合差进行计算检验、独立观测边闭合环的各坐标分量闭合差应该符合式(1)规定:
| $ \left\{ \begin{array}{l} {W_x} \le 3\sqrt n \cdot \sigma \\ {W_y} \le 3\sqrt n \cdot \sigma \\ {W_z} \le 3\sqrt n \cdot \sigma \\ {W_s} \le 3\sqrt n \cdot \sigma \end{array} \right. $ | (1) |
式中,n为闭合环的边数;
5) 同一基线不同时段的重复观测基线较差应该满足式(2)规定。如果观测数据不能满足要求时,应该对成果进行全面分析,必要时进行补测或重测[9]。
| $ {\rm{d}}s \le 2\sqrt {2\sigma } $ | (2) |
数据加载好之后利用南方测绘GNSS平差处理软件对观测数据进行平差处理,基线解算之前应先对基线解算参数进行设置,参数设置完之后点击“基线解算——全部解算”进行基线向量解算。基线解算完成后点击“重复基线”“闭合环”进行查看数据解算是否合格。对于重复基线,要满足“相对较差<相对限差”“相对误差<标称精度”(标称精度为接收机的基线长度标称精度,双频接收机为5±1×10-6×D(mm),D为基线长度(km)),当满足这两点后重复基线才能合格,如果有不合格的基线要进行基线处理。对于闭合环,要满足“边长闭合差<闭合限差”“X、Y、Z坐标分量闭合差<坐标分量限差”(分量限差和闭合限差的计算按式(1)计算),当满足这两点后闭合环才会合格,如果有不合格的闭合环需要继续处理,使之合格为止。
基线解算后如有不合格重复基线和闭合环应进行处理后再解算。基线处理方法有如下几条:
1) 确定合适的历元间隔。
基线不合格时可以改变历元间隔来处理基线,点击重复基线,在相应基线部位右击鼠标,然后在弹出的“基线情况”中进行修改调整,多次改变历元间隔试验解算,直到基线解算合格。例如18201143-18301143这条基线,从图 2可以看出该基线约有3.3 km而同步观测时间97 min,如果使用历元间隔30 s来解算则共有194个历元的数据参与解算。从图 2可以看出,解算后的方差比为7.7,虽然达到了成为合格固定双差解的条件,但基线还是不合格,由于该基线较短,而参与解算的历元的数据较多,这就会使有些信号不好的数据参加解算,这就需要增大历元间隔来重新解算,将该基线的历元间隔设为60 s,则共有97个历元的数据参与解算。从图 3可以看出,解算后的方差比为23.7,方差比大大增加,进行解算后该基线合格,经过历元间隔的调整得出一个调整历元间隔的原则:对基线同步观测时间较短的,可缩小历元间隔, 让更多的数据参与解算。当同步观测时间较长时,应增加历元间隔,以减少数据参与计算的次数; 当数据周期跳跃次数较多时,应增加历元间隔,以便可以跳过中断的数据,继续计算。
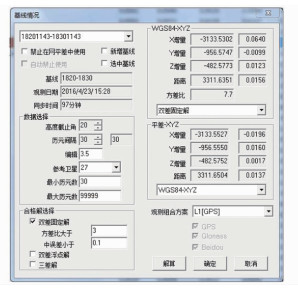 |
| 图 2 历元间隔为30 s Fig.2 The Epoch Interval Is 30 s |
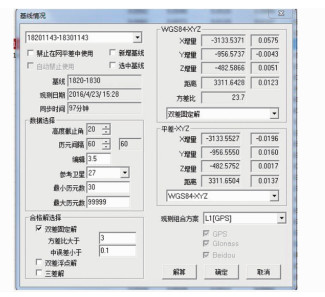 |
| 图 3 历元间隔为60 s Fig.3 The Epoch Interval Is 60 s |
虽然该实例证明改变历元间隔可以使基线解算合格,但有些基线经过调整历元间隔仍不能使基线合格,这就需要通过调整其他参数来处理不合格基线。
2) 确定合适的卫星高度截止角。
如果通过改变历元间隔不能提高方差比,则可以通过调整卫星高度的截止角来实验。当卫星高度截止角低的时候,虽然参与解算的卫星数增多,但低空卫星的信号容易被干扰且信号较弱,当卫星高度截止角大的时候,虽然参与解算的卫星数减少,但高空卫星的信号不容易被干扰而且高空卫星质量好的数据较多,这就说明卫星高度截止角不是越高越好。同样,也不是说参与解算的卫星数目越多越好,有时参与解算的卫星数少但信号质量好,解算结果反而更好,但有时因为参与解算的卫星数目太少而使解算结果反而更差,因此这就需要调整卫星高度截止角来寻找基线解算的最佳角度,使基线解算达到合格。
以18401144-18701143这条基线为例,如图 4所示将高度角设为15°时方差比为8.0,进行基线解算,该基线不合格。因此改变卫星高度截止角使之增大,如图 5所示,将高度截止角设为20°时方差比为9.2,进行基线解算,虽然高度截止角增大使得方差比增大了,但解算完后该基线还是不合格,这就需要考虑对该基线对应的卫星信号进行检查并且处理了。通过对卫星高度截止角的调整处理基线可以得出高度截止角的调整原则:当基线详解中查看到卫星数目足够多,则可以适当增大高度截止角,尽量让高空信号好的卫星参与解算; 当基线详解中查看到卫星数目不多(≥4),则可以适当减小高度截止角,让尽可能多的卫星参与解算。
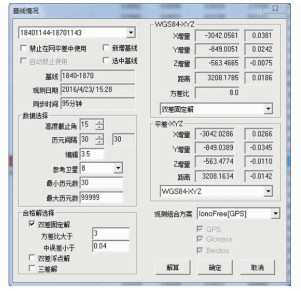 |
| 图 4 高度截止角为15° Fig.4 The High Cut-off Angle Is 15° |
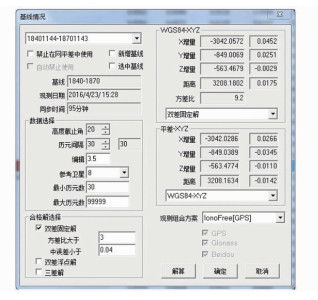 |
| 图 5 高度截止角为20° Fig.5 The High Cut-off Angle Is 20° |
3) 编辑和剔除卫星信号。如果通过改变高度截止角和历元间隔还不能够使基线解算合格,则可以找基线对应点,点击“观测数据文件”找到对应基线点,查看对应点的卫星信号情况,如果有残缺、中断的卫星信号,可以在相应卫星上面右击选择“数据编辑”,在弹出的数据编辑对话框中点击“×”对卫星信号进行选择禁止操作,对中断或者残缺的数据框起来禁止参加基线解算。在这项操作完成后点击对处理过的基线进行解算,再看重复基线是否合格。
以上3种方法应该灵活结合使用来处理基线,在用第3种方法调整的时候要注意,同一时段的数据剔除率不能大于10%,如果上面3种方法都不能使基线合格的话就需要对该点进行重测了。
闭合环不合格处理方法:闭合环超限表明有粗差的基线存在,可以先检验造成最多环不合格的基线,查阅残差图,找到原因,看是周条问题、多路径问题还是天边卫星信号问题,找到原因采取相应措施来处理存在粗差的基线,如果确实是质量问题,可以删掉该基线,再对闭合环进行解算,但需要注意的是在适当删除基线的时候不能对整个控制网造成太大的影响。在闭合环中查找影响较大的基线时,如果逐个环查找比较麻烦,这时也可以直接做无约束平差,在平差结果中找到改正数大的基线,查找原因。在进行约束网平差之前必须剔除所有包含粗差的基线,否则约束网平差结果将不正确。
通过残差图找出相应基线存在的问题,然后用处理基线的办法对相应基线进行处理,周跳问题可以通过调整高度截止角和历元间隔来处理,卫星信号问题可以通过编辑卫星信号来处理,直到合格为止,实际发现,用处理基线的3种方法并不能使所有闭合环达到合格。因此对这3种方法不能使之合格的基线可以采用删除影响较多基线的办法,使闭合环合格。
基线粗差剔除完成,闭合环解算合格后就可以进行约束网平差计算了。
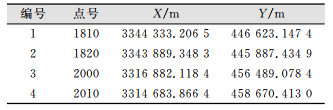
3 网平差计算结果与分析 3.1 统计分析在CPI控制网络中,共观察到38条重复基线和35个异步回路。据相关计算,所有结果均满足高速铁路规范二等GPS的限差要求。108条三维无约束平差基线分量的改正数满足规范及限差的要求。本网选取1810、1820、2000及2100这4个CPI点的平面成果作为起算点,对CPI网进行二维约束平差计算,其结果如表 4所示。
| 表 4 已知坐标(X, Y) Tab.4 Known Coordinate(X, Y) |
 |
二维约束平差最弱点平面坐标(X, Y)及精度如表 5所示,二维约束平差最弱边平面边长、方位角及其相对精度如表 6所示。
| 表 5 最弱点平面坐标(X, Y)及精度 Tab.5 Plane Coordinate (X, Y) and Accuacy of the Weakest Point |
 |
| 表 6 最弱边平面边长、方位角及其相对精度 Tab.6 Side Length, Azimuth And Relative Accuracy of the Weakest Side Plane |
 |
3.2 平差成果
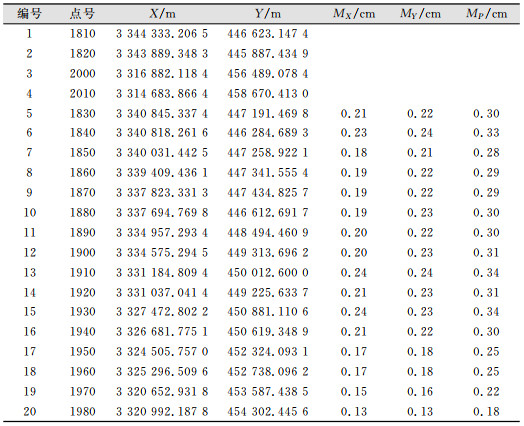
通过4个已知点1810、1820、2000、2010将采集的数据坐标进行约束平差,在GNSS数据处理软件中进行二维平差处理,平差后能够得到CPI各点的坐标值如表 7所示。
| 表 7 约束平差后各点坐标值 Tab.7 Coordinate Value of Each Point After Constrined Adjustment |
 |
3.3 复测成果分析
1) 复测与原测坐标较差限差。
根据相关规范:平面控制网复测坐标与原测坐标成果X、Y坐标分量较差的限差应小于20 mm。
CPI复测与原测相邻点间坐标差之差的相对精度按式(3)计算:
| $ \frac{{{d_s}}}{S} = \frac{{\sqrt {\Delta X_{ij}^2 + \Delta Y_{ij}^2 + \Delta Z_{ij}^2} }}{S} $ | (3) |
其中,
| $ \left\{ \begin{array}{l} \Delta {X_{ij}} = {\left( {{X_j} - {X_i}} \right)_{复}} - {\left( {{X_j} - {X_i}} \right)_{原}}\\ \Delta {Y_{ij}} = {\left( {{Y_j} - {Y_i}} \right)_{复}} - {\left( {{Y_j} - {Y_i}} \right)_{原}}\\ \Delta {Z_{ij}} = {\left( {{Z_j} - {Z_i}} \right)_{复}} - {\left( {{Z_j} - {Z_i}} \right)_{原}} \end{array} \right. $ |
式中,S为相邻点间的二维平面距离或三维空间距离; ΔXij、ΔYij分别为相邻点i与j间二维坐标差之差; ΔZij为相邻点i与j之间Z方向坐标差的差值,当只计算二维坐标差之差的相对精度时该值为零。
2) CPI的复测成果与设计成果对比。
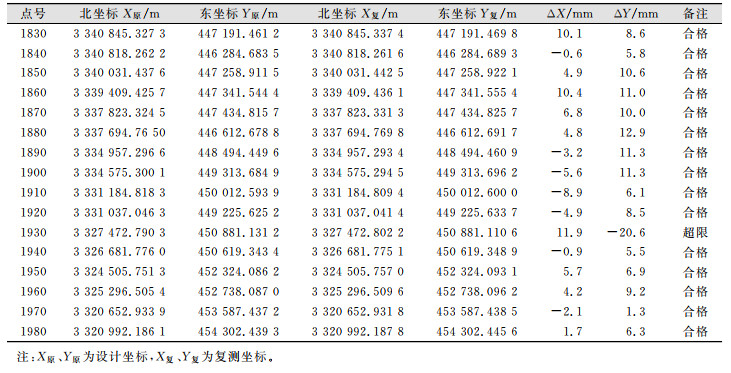
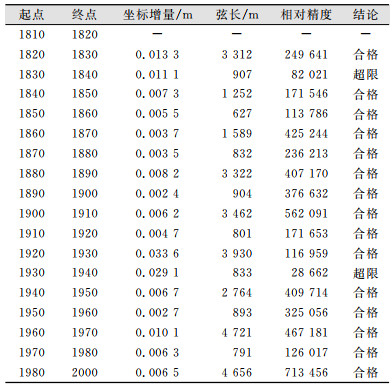
将CPI的复测成果与设计成果对比,结果如表 8所示,坐标增量的相对精度统计如表 9所示。
| 表 8 CPI复测坐标对比表 Tab.8 Comparison of CPI Retest Coordinates |
 |
| 表 9 CPI复测坐标增量相对精度统计表 Tab.9 Statistics of CPI Retest Coordinate Increment Relative Accuracy |
 |
经现场检查确认,本标段范围内单位所提供的原测CPI平面控制网桩点均保持完好,点位中心标志清晰完好,经复测和对比分析可知:
1) CPI网中除1930点外,复测坐标与原坐标的差值满足规范的要求;
2) CPI网中除1830及1930相邻点间复测与原测坐标差之差的相对精度均达到规定的限差要求; 综合分析认为1830点由于边长短导致坐标差较差超限,1930点发生位移。由此得出建议:对该网再次进行复测,看是该次复测结果不正确还是原测坐标发生位移,如果第二次复测结果还是1930点超限,则该点坐标用复测坐标; 如果第二次复测该点没超限则要检查两次复测数据和过程看是哪次复测错误再做结论。
4 结束语本文介绍了CPI控制网复测的意义,通过对控制网的概述,了解到了CPI控制网在整个工程建设中的重要性,由它的重要性可见对CPI控制网进行复测是非常有必要的,通过对原测CPI控制网网形分析,制定了作业方法,并选择仪器设备,组织调度人员对CPI网进行外业数据采集。最后用南方GNSS数据处理软件将外业采集的数据进行了数据处理,得出复测CPI网点的坐标并与原测坐标进行对比分析。结果表明CPI控制点1830点由于边长短导致坐标差较差超限,1930点发生位移,需对该网再次进行复测再做结论。取得的主要成果如下:
1) 严格按照国家GPS二等测量规范以及CPI控制网复测规范对本测区的CPI控制网进行了复测,在复测工作中选取了合适的仪器及有效的的组织人员对CPI控制网进行了外业的数据采集工作;
2) 利用南方GNSS数据处理软件严格的对采集得到的数据进行了平差处理,将平差结果与国家规范要求进行对比直到平差结果合格之后又与原测CPI控制网坐标数据进行对比得出结论,判断出了CPI控制点是否发生位移,并且给出了相应建议与结论,为后续的工程建设提供了可靠的基准控制网点。
需进一步改进的问题:本次复测采用的是6台南方S82双频接收机,选择两个时段进行测量,在数据处理过程中发现有些卫星信号非常差,因此在以后的复测过程中可以多使用几台更高精度的接收机,增加时段数来弥补这个不足之处,使得精密控制网复测数据精度更高更可靠,为高速铁路的建设提供更加准确可靠的控制网。
| [1] |
吴波, 黄博, 安江雷. 高铁CPI数据处理及控制点稳定性分析[J]. 导航定位学报, 2019, 7(1): 112-116. |
| [2] |
宣伟, 花向红, 邹进贵, 等. 成贵高铁控制网复测数据处理与稳定性分析[J]. 测绘地理信息, 2016, 41(2): 77-80+94. |
| [3] |
严丽, 黄丁发, 朱东伟. 一种高精度北斗基线解算软件的研制与性能分析[J]. 武汉大学学报·信息科学版, 2017, 42(12): 1 785-1 791. |
| [4] |
高小兵. 高速铁路基础平面控制网(CPI)复测数据处理研究[J]. 勘察科学技术, 2015(4): 19-22. |
| [5] |
吴维军, 朱洪涛, 曹娟华, 等. 高速铁路无砟轨道精调测量方法探索[J]. 铁道学报, 2018, 40(7): 136-141. |
| [6] |
李猛. 基于GPS RTK技术在高速铁路工程测量中的实践探讨[J]. 建材与装饰, 2018(19): 224-225. DOI:10.3969/j.issn.1673-0038.2018.19.184 |
| [7] |
王忠义. GPS技术与坐标转换方法在广深港高速铁路建设中的应用[J]. 铁道建筑技术, 2013(2): 92-94. |
| [8] |
姚文斌. GPS在高速铁路勘测中的应用[J]. 甘肃科技纵横, 2012, 41(4): 15-16. |
| [9] |
冯上朝. 铁路客运专线GPS首级控制网复测设计要点[J]. 山西建筑, 2010, 36(18): 356-357. |
 2021, Vol. 46
2021, Vol. 46


