| 电磁波测距三角高程代替四等水准的精度分析 |
水准测量是进行高程测量的重要手段,中国的高程控制网就是采用水准测量的方式进行的,按精度等级可以划分为一、二、三、四等水准测量[1]。在实际工程应用中,四等水准测量能满足大部分工程的高程精度要求,但四等水准测量的观测条件要求较高,如前后视距差不得大于3 m,这在工程实践中有时难以满足。三角高差测量比较灵活,因此, 用三角高程测量的方式代替四等水准测量就显得比较实用,目前,已经有部分教材和规范对该问题进行了一定的阐述。《国家三、四等水准测量规范》中对电磁波测距高程导线测量有部分阐述[2],却未明确表示可代替四等水准测量;《大地测量学基础》中概略说明了三角高程可以代替四等水准测量[3],还有少量文献采用改进的三角高程测量同等级水准进行了比较[4-9],但是适合普通工程实践的三角高程测量代替四等水准测量的精度分析,以及实际观测采用何种精度的仪器却很少有相关文献说明,这给实际应用造成了一定困惑。本文对三角高程测量误差进行了分析,并提出三角高差测量代替四等水准测量的条件。
1 高程测量误差三角高程测量通过测角和测距来间接测量出高差[10],如图 1所示。
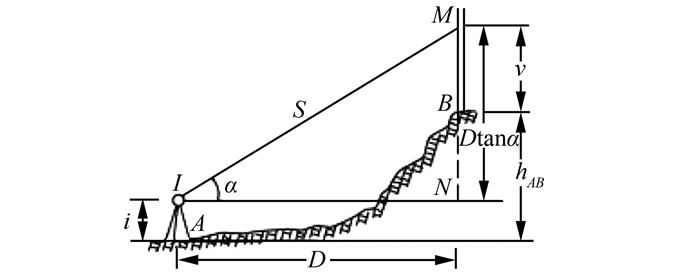 |
| 图 1 三角高程测量原理 Fig.1 Principle of Trigonometric Leveling |
A、B两点间的高差公式为:
| $ h_{A B}=S \times \sin \alpha+(1-K) \frac{S^{2}}{2 R} \cos ^{2} \alpha+i-v $ | (1) |
式中,hAB为测站与棱角之间的高差; α为竖角; S为经气象改正后的斜距; K为大气折光系数; R为地球半径; i为仪器水平轴到地面点的高度; v为反光镜瞄准中心到地面的高度。
式(1)为单向观测高差公式,其中,大气折光引起的误差和水准面不平行可以通过双向观测基本消除,简写为:
| $ m_{h}^{2}=\left(S \times \cos \alpha \times m_{\alpha}\right)^{2}+\left(\sin \alpha \times m_{s}\right)^{2}+m_{1}^{2}+m_{v}^{2} $ | (2) |
式中,mh表示整个测量高差的中误差;mα为角度测量中误差;ms为距离测量中误差。
对式(2)进行全微分,根据误差传播定律可得:
| $ m_{h}^{2}=\left(S \times \cos \alpha \times m_{\alpha}\right)^{2}+\left(\sin \alpha \times m_{s}\right)^{2}+m_{i}^{2}+m_{v}^{2} $ | (3) |
式中,mi表示仪器高测量中误差;mv表示棱角高中误差。
对向观测的误差为单向观测的
| $ \;\;\;\;\;\;\;\;\;\;\;m_{h}=\\ \sqrt{1 / 2\left(\left[\left(S \times \cos \alpha \times m_{\alpha}\right)^{2}+\left(\sin \alpha \times m_{s}\right)^{2}+2 m_{q}^{2}\right]\right)^{2}} $ | (4) |
从式(4)可以看出,测量的高差误差与视线长度、垂直角大小、仪器测角测距精度、仪器和棱角高量测精度相关。
2 精度计算分析 2.1 高差中误差计算式(4)中各项误差特点如下:
1) 当前电磁波的测距精度普遍能达到2+2×10-6 mm。
2) 相关文献对仪器高的测量进行了一些有益的研究[11],但是实际操作中限制较多。目前在测量实践中,可以通过多次测量将仪器和棱角高的测量中误差控制在2 mm。
从以上分析可知,仪器和棱角高的测量误差可以通过先验误差确定,高差的测距中误差的变量因素主要有视线长度、测角中误差和视线垂直角。分别对不同的视线长度、垂直角和测角中误差进行计算,进而计算出高差中误差mh。
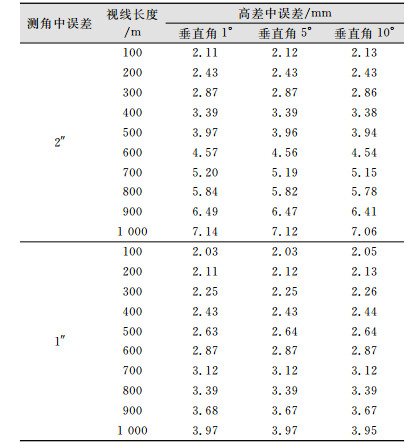
当测角中误差为2″和1″时,根据式(4)对不同的视线长度和垂直角进行计算,结果如表 1所示。
| 表 1 按测角中误差为2″和1″计算的高差中误差 Tab.1 2″ and 1″ Angle Error to Calculate Middle Error |
 |
2.2 高差中误差统计分析
通过高差中误差的来源和实际计算分析,可以得出以下结论:
1) 垂直角大小对高差中误差的影响很小。从表 1可以看出,当仪器的测角中误差和视线长度一致,实际测量中的垂直角改变时,高差中误差的变动很小,可以忽略不计。
2) 高差中误差随视线长度增大而增大。从表 1可以看出,当视线长度增大时,高差中误差逐渐增大,并且增大幅度在加快。
3) 仪器测角中误差越小,高差中误差越小。从表 1可以看出,当视线长度和垂直角大小一样时,仪器的测角中误差小,则高差中误差小;当视线长度较大时,仪器测角中误差对高差中误差的影响更为明显。
4) 当视线长度较小时,仪器和棱角高的量测误差对高差中误差影响较大。从表 1可以看出,当视线长度小于300 m时,高差中误差都小于3 mm,其中主要误差是仪器和棱角高的2 mm测量误差。
综上所述,高差中误差主要和仪器测角精度、视线长度、仪器高和棱角高的量测精度有关,和垂直角大小基本无关,结合表 1数据用图 2表示。
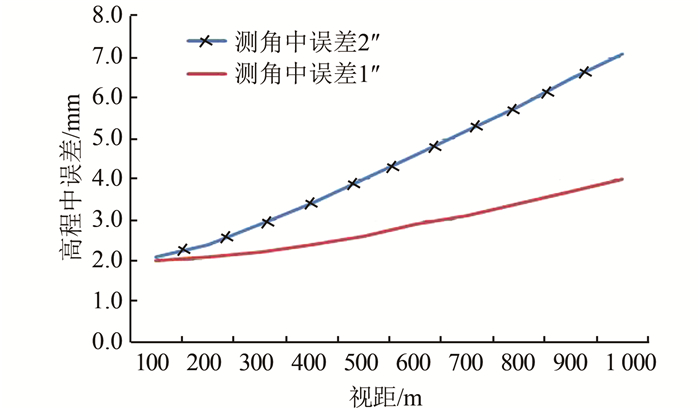 |
| 图 2 视线长度、测角中误差和高差中误差关系 Fig.2 Relation Between the Sight Length, Angle and Height Middle Error |
《国家三、四等水准测量规范》中规定四等水准测量的每km偶然中误差为5 mm,由图 2可以看出,测角中误差为2″的仪器在视距长度较大时不能满足要求,测角中误差为1″时可以满足要求。因此,当采用测角中误差为1″或更高精度的仪器时,采用对向观测,则可用电测波三角高程测量代替四等水准测量。
3 结束语根据三角高程测量的误差传播特点,本文分析了三角高程测量的误差来源和精度,并进行了数据分析。计算结果显示,垂直角在一定范围内,对高差中误差的影响可以忽略不计,高差中误差主要和仪器测角精度、视线长度和仪器量测精度有关,当采用测角中误差为1″或更高精度的仪器,通过对向观测、认真测量仪高等手段,可用三角高程测量代替四等水准测量。该研究对今后的三角高程测量代替四等水准测量工程实践具有一定的参考价值。
| [1] |
国家测绘局.国家大地测量基本技术规定: GB 22021-2008[S].北京: 中国标准出版社, 2008
|
| [2] |
国家测绘局测绘标准化研究所.国家三、四等水准测量规范: GB/T 12898-2009[S].北京: 中国标准出版社, 2009
|
| [3] |
孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2006.
|
| [4] |
卢群, 邱卫宁, 范玉磊, 等. 长距离跨海高程传递测量方法研究与工程实践[J]. 测绘地理信息, 2016, 41(1): 70-73. |
| [5] |
刘冠兰, 杨川, 崔国立. 高原地区精密三角高程测量实践[J]. 测绘地理信息, 2016, 41(5): 12-16. |
| [6] |
杜宁, 王莉. 连续中间法三角高程测量权的探讨[J]. 测绘科学, 2012(3): 142-143. |
| [7] |
吴迪军, 许提多, 罗苏. 关于三角高程跨河水准测量限差的探讨[J]. 地理空间信息, 2012, 10(5): 105-107. |
| [8] |
方明, 武威. 跨海高程传递三角高程数据处理及质量分析[J]. 海洋测绘, 2012, 32(5): 53-55. DOI:10.3969/j.issn.1671-3044.2012.05.016 |
| [9] |
黄保存. 水电站高程控制测量方法的分析与探讨[J]. 云南水利发电, 2015, 31(5): 135-138. |
| [10] |
潘正风, 杨正尧, 程效军, 等. 数字测图原理与方法[M]. 武汉: 武汉大学出版社, 2004.
|
| [11] |
王涛, 田林亚, 魏玉明, 等. 高精度仪器高量取方法研究[J]. 测绘通报, 2017(1): 144-146. |
 2020, Vol. 45
2020, Vol. 45

