| 附加主方向判定的PCA点云数据初始配准算法 |
2. 青海省地理信息中心,青海 西宁,810001;
3. 青海地理信息产业发展有限公司,青海 西宁,810000
2. Provincial Geomatics Center of Qinghai, Xining 810001, China;
3. Qinghai Geographic Information Industry Development Co., Ltd., Xining 810000, China
近年来,地面三维激光扫描技术在数字城市、逆向建模、文物保护、交通规划乃至新兴的3D打印技术等领域具有重大应用前景[1],点云数据处理是三维激光扫描技术的核心,而点云数据配准[2]作为点云数据处理的重要环节直接影响后续三维建模等其他应用环节的精度。对此,国内外专家学者进行大量研究,相继提出了多种配准方法[3-6],取得了丰富的研究成果,但各类算法依然存在一定的不足与局限,严重制约了三维激光扫描技术在精密建模和变形监测等领域的拓展应用[7]。目前,三维激光扫描数据初始配准主要分为手动配准和自动配准两种方式,手动初始配准是指采用人机交互的方式提取扫描数据的公共点,该方法自动化程度低,且操作人员应具有一定的专业基础,配准精度完全取决于公共点的精度。自动初始配准是指通过检测两片点云的公共特征来完成的,自动初始配准方法又可以分为两类[8]:①通过计算点云的法矢和曲率等高阶微分信息检测公共特征,该类方法计算量大且对噪声比较敏感,只针对某些少数类型的数据有效; ②将三维点云数据转换成二维数字图像,在二维数字图像上采用特征检测算子检测公共特征,该类方法算法实现比较复杂。
主成分分析(principal component analysis,PCA)是指通过降维的方法将数据的多重指标转换为少数几个主要的综合性指标,进而利用几个较少的变量研究整个数据集,实现化繁为简的一种数据处理算法[9-11]。主成分分析算法具有概念简单、计算简洁、易于编程实现等优点和特点,被广泛用于统计学、数学建模、数量地理学和分子动力学等各学科领域,该算法需要先构建数据集的协方差矩阵,再由协方差矩阵的特征值及其特征向量确定各个成分量,然后在总方差不变的前提下进行数学变换,最后以具有最大方差的变量作为第一主成分,以方差第二大的变量作为第二主成分,以此类推至方差第n大的变量作为第n主成分。本文将PCA算法引入三维激光扫描数据的初始配准,并以三维空间向量数量积为基础对标准主成分分析算法配准的主轴向量指向判定问题进行研究,提出一种附加主方向判定条件的PCA点云数据初始配准算法。
1 附加主方向判定的PCA初始配准算法标准主成分分析配准算法是先计算两片点云数据的重心坐标和协方差矩阵,再分别计算协方差矩阵的特征值及其特征向量,将特征值从大到小进行排序,以重心坐标作为新坐标系的原点,最大特征值对应的特征向量作为第一主方向X轴,次最大特征值对应的特征向量作为第二主方向Y轴,以X和Y进行叉乘处理得到Z轴,建立O-XYZ右手坐标系。最后通过两片点云数据计算新旧坐标系之间的旋转矩阵和平移参数。基于主成分分析算法的点云初始配准的具体步骤如下:
1) 将两片点云数据集P ={P1, P2, …, Pi}和Q ={Q1, Q2, …, Qi}进行坐标重心化:
| $ \left\{ \begin{array}{l} {O_P} = \frac{1}{i}\sum\limits_{m = 1}^i {{P_m}} \\ {O_Q} = \frac{1}{j}\sum\limits_{m = 1}^i {{Q_m}} \end{array} \right. $ | (1) |
式中,OP 为(OPx,OPy,OPz),OQ 为(OQx,OQy,OQz)。
2) 构造数据集P、Q的协方差矩阵RP 和RQ 分别为:
| $ {\boldsymbol{R}_\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{m = 1}^i {{{({x_m} - {O_{Px}})}^2}} }&{\sum\limits_{m = 1}^i {({x_m} - {O_{Px}})({y_m} - {O_{Py}})} }&{\sum\limits_{m = 1}^i {({x_m} - {O_{Px}})({z_m} - {O_{Pz}})} }\\ {\sum\limits_{m = 1}^i {({y_m} - {O_{Py}})({x_m} - {O_{Px}})} }&{\sum\limits_{m = 1}^i {{{({y_m} - {O_{Py}})}^2}} }&{\sum\limits_{m = 1}^i {({y_m} - {O_{Py}})({z_m} - {O_{Pz}})} }\\ {\sum\limits_{m = 1}^i {({z_m} - {O_{Pz}})({x_m} - {O_{Px}})} }&{\sum\limits_{m = 1}^i {({z_m} - {O_{Pz}})({y_m} - {O_{Py}})} }&{\sum\limits_{m = 1}^i {{{({z_m} - {O_{Pz}})}^2}} } \end{array}} \right] $ | (2) |
| $ {\boldsymbol{R}_\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{m = 1}^j {{{({x_m} - {O_{Qx}})}^2}} }&{\sum\limits_{m = 1}^j {({x_m} - {O_{Qx}})({y_m} - {O_{Qy}})} }&{\sum\limits_{m = 1}^j {({x_m} - {O_{Qx}})({z_m} - {O_{Qz}})} }\\ {\sum\limits_{m = 1}^j {({y_m} - {O_{Qy}})({x_m} - {O_{Px}})} }&{\sum\limits_{m = 1}^j {{{({y_m} - {O_{Qy}})}^2}} }&{\sum\limits_{m = 1}^j {({y_m} - {O_{Qy}})({z_m} - {O_{Qz}})} }\\ {\sum\limits_{m = 1}^j {({z_m} - {O_{Qz}})({x_m} - {O_{Qx}})} }&{\sum\limits_{m = 1}^j {({z_m} - {O_{Qz}})({y_m} - {O_{Qy}})} }&{\sum\limits_{m = 1}^j {{{({z_m} - {O_{Qz}})}^2}} } \end{array}} \right] $ | (3) |
3) 计算协方差矩阵对应的特征值及其特征向量,将两个矩阵的特征值从大到小排列,即VP1、VP2、VP3和VQ1、VQ2、VQ3。令VPx=VP1、VPy=VP2、VPz=VP1×VP2、VQx=VQ1、VQy=VQ2、VQz=VQ1×VQ2,再分别以OP和OQ作为坐标系原点,以VPx、VPy、VPz及VQx、VQy、VQz作为坐标轴,建立两个点集新的坐标系OP-VPxVPyVPz、OQ-VQxVQyVQz。
4) 通过新构建的坐标系解算两片点云的坐标旋转矩阵,先将两个坐标系的坐标轴单位化,得到其主成分矩阵分别为:
| $ {\boldsymbol{M}_\boldsymbol{P}} = {\left[ {\begin{array}{*{20}{c}} {\frac{{{V_{Px}}}}{{\left\| {{V_{Px}}} \right\|}}}&{\frac{{{V_{Py}}}}{{\left\| {{V_{Py}}} \right\|}}}&{\frac{{{V_{Py}}}}{{\left\| {{V_{Py}}} \right\|}}} \end{array}} \right]^{\rm{T}}} $ | (4) |
| $ {\boldsymbol{M}_\boldsymbol{Q}} = {\left[ {\begin{array}{*{20}{c}} {\frac{{{V_{Qx}}}}{{\left\| {{V_{Qx}}} \right\|}}}&{\frac{{{V_{Qy}}}}{{\left\| {{V_{Qy}}} \right\|}}}&{\frac{{{V_{Qy}}}}{{\left\| {{V_{Qy}}} \right\|}}} \end{array}} \right]^{\rm{T}}} $ | (5) |
由两个点集之间的变换关系可知:
| $ {\boldsymbol{M}_\boldsymbol{Q}} = {\boldsymbol{M}_\boldsymbol{P}} \cdot \boldsymbol{R} $ | (6) |
其中,
| $ \boldsymbol{R} = \boldsymbol{M}_\boldsymbol{P}^{ - 1} \cdot {\boldsymbol{M}_\boldsymbol{Q}} $ |
5) 利用计算的旋转矩阵通过式(7)计算平移矩阵T。
| $ \boldsymbol{T} = {\boldsymbol{O}_\boldsymbol{Q}} - {\boldsymbol{O}_\boldsymbol{P}} \cdot \boldsymbol{R} $ | (7) |
尽管标准主成分分析配准算法原理简单、易于实现,其核心思想是将两片点云数据的主轴坐标系直接对齐,进而实现点云数据的配准,此时两片点云的主轴分别对应在数据集的相同部位,但该算法并未顾及协方差矩阵计算的特征向量存在正、负两个方向的现象,也未顾及初始配准时两个点云数据集间存在大旋转角偏差的现象,若未对主方向进行判定和调整,配准时会对应到点云数据的相反部位,造成配准结果失真。
设第一片点云的第一主方向X1和第二主方Y1组成的坐标系为O-X1Y1,第二片点云的第一主方向X2和第二主方向Y2组成的坐标系为O-X2Y2,若两片点云的第一主方向相反、第二主方向指向一致,则分别对两个主方向的向量进行叉乘运算,得到第三个主方向Z1和Z2,如图 1所示。
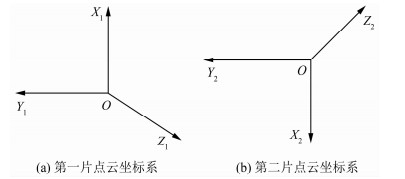 |
| 图 1 3方向主轴坐标系图 Fig.1 Three-Direction Spindle Coordinate System |
分析图 1可知,主轴(Y1与Y2)指向了数据集中的相同位置,但第一主方向(X1与X2)和第三主方向轴(Z1与Z2)完全指向了相反的方向。因此配准结果失真,必须对主轴的方向进行判断和调整。
在空间解析几何中,向量的数量积是用于判定两个空间向量指向的评价指标,如果两个向量的数量积大于零,则说明他们的方向一致或者相近; 如果两个向量的数量积小于零则说明他们的方向相反或者相差较大。为了对主轴的方向进行判断和调整,以三维空间向量的数量积[12]为基础,在计算两片点云数据的第一主方向(VP1、VQ1)和第二主方向(VP2、VQ2)基础上,分别判定VP1与VQ1、VP2与VQ2的方向一致性,根据数量积的正负将目标点集P的两个主方向调整到与参考点集Q的两个主方向相互一致的方向(即若VP1·VQ1<0,则令VP1=-VP1,反之VP1保持不变; 若VP2·VQ2<0,则令VP2=-VP2,反之VP2保持不变),再用经过判定和调整后的第一和第二主方向计算第三主方向(即VP3=VP1×VP2、VQ3=VQ1×VQ2),组成新的主轴坐标系参与配准参数的解算。
2 实例应用与分析为了验证附加主方向判定的主成分分析初始配准算法的应用效果,采用Trimble SX10地面激光扫描仪对某工业构件进行扫描,共获得54 139个点云数据,其初始配准后的三维显示效果如图 2所示。对原始数据进行一组固定大角度旋转和平移操作,具体为将原始点云分别绕X、Y、Z轴旋转120°、108°、150°,X、Y、Z方向分别平移5 m、6 m、7 m,旋转和平移后的三维显示效果如图 3所示。
 |
| 图 2 构件三维点云显示图 Fig.2 Component 3D Point Cloud Display |
 |
| 图 3 原始点集P与变换后的点集Q Fig.3 Original Point Set P and Transformed Point Set Q |
设原始点云数据集为P,旋转平移变换后的点云数据集为Q,分别采用标准PCA配准算法和本文提出的附加主方向判定的PCA配准算法将点集P配准到点集Q。由大角度旋转矩阵公式解算的旋转矩阵R与T分别为:
| $ \begin{array}{l} \boldsymbol{R} = \left[ {\begin{array}{*{20}{c}} {0.2676}&{0.1545}&{0.9511}\\ { - 0.4633}&{0.8448}&{0.2676}\\ {0.8448}&{0.5122}&{0.1545} \end{array}} \right];\\ \boldsymbol{T} = {\left[ {\begin{array}{*{20}{c}} {5.0000}&{6.0000}&{7.0000} \end{array}} \right]^{\rm{T}}} \end{array} $ |
根据式(1)计算两片点云的重心坐标分别为OP=(-21.900 0,-79.474 1,-32.947 3)和OQ=(42.753 3,-42.179 4,-57.302 2)。根据式(2)、式(3)计算的两片点云的协方差矩阵分别为:
| $ \begin{array}{l} {\boldsymbol{R}_P} = 1 \times {10^8} \times \left[ {\begin{array}{*{20}{c}} {2.0206}&{0.0041}&{0.0332}\\ {0.0041}&{2.0179}&{0.0203}\\ {0.0332}&{0.0203}&{1.1099} \end{array}} \right];\\ {\boldsymbol{R}_Q} = 1 \times {10^8} \times \left[ {\begin{array}{*{20}{c}} {1.1855}&{ - 0.2335}&{0.0984}\\ { - 0.2335}&{1.9493}&{0.0284}\\ {0.0984}&{0.0284}&{2.0136} \end{array}} \right] \end{array} $ |
分别计算两个协方差矩阵的特征值及其特征向量,将特征值从小到大排列,对应的特征向量按式(4)、式(5)分别构建主轴特征向量矩阵:
| $ \begin{array}{l} {\boldsymbol{M}_P} = {\left[ {\begin{array}{*{20}{c}} {{V_{P1}}}&{{V_{P2}}}&{{V_{P3}}} \end{array}} \right]^{\rm{T}}} = \\ \left[ {\begin{array}{*{20}{c}} { - 0.8188}&{ - 0.5730}&{0.0363}\\ { - 0.5726}&{0.8195}&{0.0222}\\ { - 0.0424}&{ - 0.0026}&{ - 0.9991} \end{array}} \right];\\ {\boldsymbol{M}_\boldsymbol{Q}} = {\left[ {\begin{array}{*{20}{c}} {{V_{Q1}}}&{{V_{Q2}}}&{{V_{Q3}}} \end{array}} \right]^{\rm{T}}} = \\ \left[ {\begin{array}{*{20}{c}} {0.0903}&{ - 0.2775}&{ - 0.9565}\\ {0.0931}&{0.9586}&{ - 0.2693}\\ {0.9916}&{ - 0.0647}&{0.1124} \end{array}} \right] \end{array} $ |
将两片点云的3个主成分轴分别展示在各自的点云数据中,如图 4所示。
 |
| 图 4 主成分轴显示图 Fig.4 Principal Component Axis Display |
按标准主成分分析配准算法将主轴(VP1,VP2,VP3)与(VQ1,VQ2,VQ3)对齐,计算坐标系OP-VP1VP2VP3与OQ-VQ1VQ2VQ3之间的旋转矩阵R和平移向量T:
| $ \begin{array}{c} \boldsymbol{R} = \boldsymbol{M}_P^{ - 1} \cdot {\boldsymbol{M}_Q} = \\ \left[ {\begin{array}{*{20}{c}} {0.0504}&{ - 0.3003}&{0.9525}\\ { - 0.6352}&{0.7263}&{0.2626}\\ { - 0.7707}&{ - 0.6183}&{ - 0.1542} \end{array}} \right];\\ \boldsymbol{T} = {\boldsymbol{O}_\boldsymbol{Q}} - \boldsymbol{R} \cdot {\boldsymbol{O}_\boldsymbol{P}} = \\ {\left[ {\begin{array}{*{20}{c}} {51.3730}&{10.2860}&{ - 128.3960} \end{array}} \right]^{\rm{T}}} \end{array} $ |
可以看出旋转矩阵R与平移向量T的计算结果与设置的旋转平移参数式相差很大,将计算的旋转矩阵和平移参数应用于点集P,效果如图 5所示。
 |
| 图 5 基于传统PCA算法的点云配准结果 Fig.5 Point Cloud Registration Result Based on Traditional PCA Algorithm |
分析图 5可知,基于标准PCA的配准结果出现了明显的错误现象,两片点云的第一主方向存在较大差异,第二主方向差异不大。因此,根据上文对第一和第二主方向的判定方法,分别对计算的两片点云数据所对应的第一和第二主成分方向向量的数量积正负进行判断,即VP1=-VP1=-0.169 0<0、VP2·VQ2=0.944 0>0,令VP1=-VP1,VP2保持不变,重新计算VP3,将经过判定和调整后的主轴方向展示到各自的点云图上,效果如图 6所示。
 |
| 图 6 调整后的主成分轴显示图 Fig.6 Adjusted Principal Component Axis Display |
分析图 6可知,经过调整后的两个点集的主轴方向都分别对应了各自相同的部位,且计算的旋转矩阵和平移参数结果表明与开始设置的参数在数值上保持一致,将计算的转换参数应用于点集P,如图 7所示。
 |
| 图 7 调整主轴后的配准效果 Fig.7 Adjust the Registration Effect After the Spindle |
分析图 7可知,两片点云数据完全融合,说明运用主轴调整后的PCA配准算法可以达到很好的配准效果,可以为后期的精确配准提供良好的初始位置。
3 结束语三维激光扫描数据配准要保证其正确性与准确性,本文针对海量三维激光扫描数据的配准,在分析基于标准PCA的点云初始配准算法原理及其处理流程的基础上,指出了标准PCA算法由于在大角度情况下对主轴方向缺少判断和调整致使配准产生错误,对此提出了附加主方向判定条件的改进PCA配准算法。利用Matlab编程将所提算法程序化,以Trimble SX10地面激光扫描仪对某大型工业构件扫描的数据作为研究对象,验证了附加主方向判定的PCA初始配准算法能实现较好的配准效果,可以为后续精确配准提供良好的初始位置。
| [1] |
花向红, 赵不钒, 陈西江, 等. 地面三维激光扫描点云质量评价技术研究与展望[J]. 地理空间信息, 2018, 16(8): 1-7. DOI:10.3969/j.issn.1672-4623.2018.08.001 |
| [2] |
盛庆红, 张斌, 肖晖, 等. 直线簇约束下的地面LiDAR点云配准方法[J]. 武汉大学学报·信息科学版, 2018, 43(3): 406-412. |
| [3] |
唐志荣, 刘明哲, 蒋悦, 等. 基于典型相关分析的点云配准算法[J]. 中国激光, 2019, 46(1): 17-19. |
| [4] |
张谦, 李梦瑶, 成晓强. 几何刚性何法向量采样一致性的点云配准算法[J]. 测绘科学, 2019, 42(1): 112-117. |
| [5] |
李仁忠, 杨曼, 田瑜, 等. 基于ISS特征点结合改进ICP的点云配准算法[J]. 激光与光电子学进展, 2017, 48(11): 312-319. |
| [6] |
刘美菊, 王旭东, 李凌燕, 等. 改进的RANSAC算法在三维点云配准中的应用[J]. 激光与光电子学进展, 2018, 47(5): 165-171. |
| [7] |
朱曙光, 何宽, 周建郑. 徕卡三维激光扫描系统在建筑物精细建模中的应用[J]. 测绘通报, 2018, 64(2): 154-156. |
| [8] |
熊风光. 三维点云配准技术研究[D]. 太原: 中北大学, 2018
|
| [9] |
丁鸽, 赵若鹏, 卞磊, 等. 基于离群点探测准则和主成分分析的点云平面拟合效果研究[J]. 测绘地理信息, 2017, 42(03): 25-28. |
| [10] |
李志学, 莫文波, 周松林, 等. 空间主成分分析的城市生活便利度指数研究——以长沙市为例[J]. 测绘地理信息, 2021, 46(2): 110-115. |
| [11] |
丁鸽, 赵若鹏, 卞磊, 等. 基于离群点探测准则和主成分分析的点云平面拟合效果研究[J]. 测绘地理信息, 2017, 42(3): 25-28. |
| [12] |
黄延祝, 成孝予. 线性代数与空间解析几何(第二版)[M]. 北京: 高等教育出版社, 2003: 74-75.
|
 2021, Vol. 46
2021, Vol. 46

