| GPS与InSAR形变结果融合分析 |
在合成孔径雷达干涉测量(interferometric synthetic aperture radar, InSAR)数据处理中,目前已经发展了多类InSAR技术,这些InSAR技术已广泛应用于各种大面积的变形监测中,如火山、地震、地面沉降、地裂缝和滑坡等。InSAR技术获取的仅是雷达到地面视线方向的一维形变信息,而很多灾害大多表现为二维甚至三维形变,为真实反映地表形变的实际情况,需要研究融合多源数据的二三维形变反演。InSAR技术的时间分辨率较低,对ENVISAT卫星而言,重复周期为35 d,在监测过程中会丢失许多形变和位移信息,因而对对象的认识不够完整,导致测绘工作者难以抉择或者做出错误的判断。InSAR容易受到大气层延迟(对流层延迟、电离层延迟)、卫星轨道误差和地表状况的影响,导致图像解释错误,以及地面散射去相关和时变去相关,同时过多的相位噪声会大大降低干涉结果的可靠性,并增加干涉相位解缠难度[1]。
全球定位系统(global positioning system,GPS)技术发展至今,在定位导航领域中已经相当成熟,定位结果可精确至毫米级,能精确地确定电离层和对流层参数并可实时监测,具有较高的时间分辨率,采样率为10~20 Hz。GPS技术为应用最广泛的空间大地测量手段,已经应用于建筑物、大坝等重要工程的变形监测以及车辆、飞机等动态目标的实时寻址。GPS定位可以高精度获取三维形变信息,但其空间分辨率很低,可能是几十或几百公里,为离散点定位,得不到连续的定位结果,以至于丢失诸多空间信息[2]。
星载合成孔径雷达(synthetic aperture radar, SAR)获取的图像虽然经过永久散射体(permanent sca-tterers, PS)和小基线技术处理方法提高了干涉对之间的相干性,以及大面积获取图像能力提高了空间分辨率,但是最终结果只是参考点间的相对形变量;GPS技术虽然可实时监测地表变化,提高了时间相干性,但是最终结果只是稀疏点的绝对坐标[3]。为了综合这两种技术的优势,并获得大面积高相干点较为可靠的形变,有必要将GPS的监测结果与InSAR的监测结果相融合进行网平差解算[4, 5]。
1 GPS与InSAR融合网平差原理因为InSAR一维形变监测中缺少参考基准,所以笔者引入同期GPS观测结果,以提供高精度的三维形变信息,用研究区内多个GPS形变信息来约束InSAR视线方向的形变,最终获得InSAR三维形变结果。假设在第m个干涉图中,像素坐标为(i,j)的点解缠相位φi, jm为:
| $ \varphi _{i,j}^m = \varphi _{{\rm{topo}},i,j}^m + \varphi _{{\rm{def}},i,j}^m + \varphi _{{\rm{atm,}}i,j}^m + \varphi _{{\rm{orb}},i,j}^m + \varphi _{{\rm{noi}},i,j}^m $ | (1) |
式中, φtopo, i, jm表示与地形有关的相位误差;φdef, i, jm表示地表形变相位;φatm, i, jm表示与大气延迟有关的相位误差;φorb, i, jm为由轨道误差引起的相位;φnoi, i, jm包含了热噪声、失相干等误差。
在第m个干涉组合网点中,相邻两点(i,j)和(k,l)的相位差可表示为:
| $ \Delta \varphi _{(i,j)\left( {k,l} \right)}^m = \alpha _{i,j}^m\Delta {h_{(i,j)\left( {k,l} \right)}} + {\beta ^m}\Delta {v_{(i,j)\left( {k,l} \right)}} + \omega _{(i,j)\left( {k,l} \right)}^m $ | (2) |
式中,Δh(i, j)(k, l)为相邻两点的高程误差的差值;Δv(i, j)(k, l)为相邻两点的形变量的差值;αi, jm为高程误差系数;βm为形变量系数;ω(i, j)(k, l)m包含噪声误差、轨道误差与大气延迟误差。在空间上,轨道误差和大气延迟误差具有强相关性,因此笔者根据一定的距离构建的相邻点之间的轨道误差和大气延迟误差非常小,甚至可以忽略不计。同时,对相干性很高的点来说,噪声误差也比较小,因此,笔者将ω(i, j)(k, l)m看做均值为0的随机函数[1, 6]。
如果所研究区域一共有M景影像,利用相应的短基线规则生成了n组干涉组合,那么可知相邻两点之间的相位差为:
| $ \Delta {\varphi _{(i,j)\left( {k,l} \right)}} = \mathit{\boldsymbol{A}}\left[ \begin{array}{l} \Delta {h_{(i,j)\left( {k,l} \right)}}\\ \Delta {v_{(i,j)\left( {k,l} \right)}} \end{array} \right] + {\omega _{(i,j)\left( {k,l} \right)}} $ | (3) |
式中,A =[αi, jm βm]。
对于采用选定的点所组成的三角网来说,三角网中的每条边都可以建立式(3)的相位差方程,从而采用最小二乘平差求得基线参数Δh和Δv[7, 8]为:
| $ \left[ \begin{array}{l} \Delta h\\ \Delta v \end{array} \right] = {\left( {{\mathit{\boldsymbol{A}}^{\rm T}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}\Delta \mathit{\boldsymbol{\varphi }} $ | (4) |
式中,P为观测值权矩阵;Δh为任意两点高程误差的差值;Δv为任意两点形变量的差值。
如果通过式(4)计算由选定点所组成的三角网的基线参数,必须在一定的基准条件下进行网平差,即从已知的参考点出发对整个网平差,得到各个点的形变速率和高程改正。设整个网中一共有Q个点,组合形成N条基线,网中各点的参数矩阵为X,基线与点的关系矩阵为G,G中的每行代表一条基线,则函数关系式变为:
| $ \mathit{\boldsymbol{L = }}\left[ {\Delta \mathit{\boldsymbol{V}}\;\;\;\;\Delta \mathit{\boldsymbol{H}}} \right] = \mathit{\boldsymbol{GX}} $ | (5) |
式中,ΔV =[Δv1 Δv2 … ΔvN]T; ΔH =[Δh1 Δh2 … ΔhN]T。
将有GPS先验信息的点作为平差的参考点,其在G矩阵中对应的列是si,令LL= L-sixi,去掉与GPS参考点相关的si、xi后形成的矩阵表示为GG、XX,则有:
| $ {\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{L}}}{\rm{ = }}{\mathit{\boldsymbol{G}}_\mathit{\boldsymbol{G}}}{\mathit{\boldsymbol{X}}_\mathit{\boldsymbol{X}}} $ | (6) |
当GPS参考点的个数Y>1时,可在观测方程中增加约束条件:
| $ \mathit{\boldsymbol{CX}} = {\mathit{\boldsymbol{W}}^{\rm{T}}} = 0 $ | (7) |
式中,C表示剩下Y-1个GPS参考点的基线设计矩阵;WT为先验信息,可以通过已知的地面观测数据获得。则经过约束点的最小二乘解为[9-11]:
| $ \mathit{\boldsymbol{X}} = (\mathit{\boldsymbol{N}}_\mathit{\boldsymbol{G}}^{ - 1} - \mathit{\boldsymbol{N}}_\mathit{\boldsymbol{G}}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N}}_\mathit{\boldsymbol{C}}^{ - 1}\mathit{\boldsymbol{CN}}_\mathit{\boldsymbol{G}}^{ - 1})\mathit{\boldsymbol{Z}} + \mathit{\boldsymbol{N}}_\mathit{\boldsymbol{G}}^{ - 1}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{N}}_\mathit{\boldsymbol{C}}^{ - 1}{\mathit{\boldsymbol{W}}^{\rm{T}}} $ | (8) |
式中,NG = GGTPPGG,其中PP = ATPA;Z = GGTPPLL;NC= CNG-1CT。
2 实验分析 2.1 资料介绍已有数据为西安地区2009-05-2010-06一年时间跨度的33张解缠图以及2009-06和2010-05测算的4个GPS绝对高程。
干涉图位于SAR坐标系下,相位值已经经过解缠、去除趋势项减弱轨道误差,经过滤波处理弱化大气效应的影响。干涉图的命名格式为:时间1_时间2,如090523_090627。干涉对的时间跨度最短为34 d,最长为384 d。因GPS点位于地理坐标系,需要地理编码进行坐标系的统一。
处理目标:得出一年内稳定PS点间的相对形变速率,结合已有GPS点的绝对形变量,网平差得出各PS点的绝对形变量,即一年内的年形变速率。
处理流程:输入一定数量的解缠图与相干图,对PS点进行识别与提取,构建三角网,解算形变速率与高程误差,求解PS点之间的相对形变,采用GPS数据做约束求解各个PS点的绝对形变。以不同时间作为主影像的InSAR形变时间序列,结果如图 1所示,GPS点分布如图 2所示,图中黄色点显示了4个GPS点的位置,黑红色点为InSAR相干点,共包含7 092个点。GPS点与InSAR相干点通过插值方法选择为同一点。
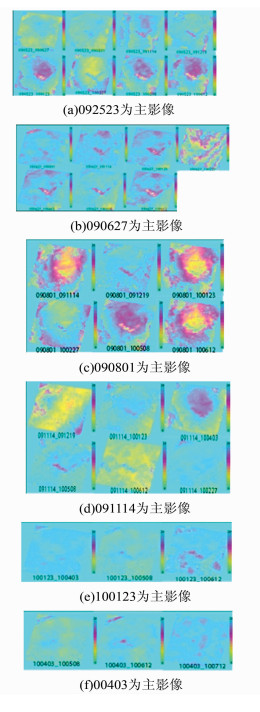 |
| 图 1 不同时间作为主影像的相位解缠图 Figure 1 Phase Unwrapping Maps of Different Main Images |
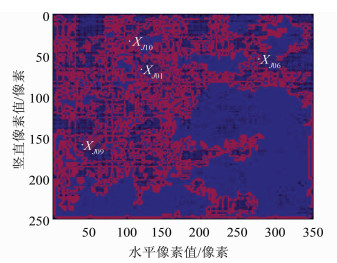 |
| 图 2 GPS点分布图 Figure 2 GPS Points Distribution |
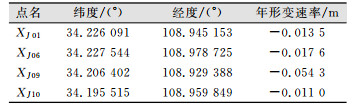
实验数据为7 092个PS点、21 064个弧段以及4个GPS控制点。控制点数据具体如表 1所示。
| 表 1 控制点的经纬度及其年形变速率 Table 1 Latitude and Longitude of the Control Points and Its Deformation Rate |
 |
2.2 实际数据实验
在用模拟数据成功调试程序的基础上,用实测数据在具有不同数量GPS点约束下分别进行实验,将不同约束个数解算所得的已知GPS点形变速率与其已知形变速率进行比较,作为解算好坏程度的一个指标。
当分别以1个点XJ01、2个点XJ01和XJ09、3个点XJ01、XJ09和XJ06做约束时,计算得其他GPS点的形变速率以及形变速率差如表 2所示,解算其他InSAR相干点的形变速率如图 3所示,图 3中横坐标与纵坐标分别表示在SAR坐标系下的行号与列号,图中描绘出了形变速率等值线,并且用不同的灰度值填充整个区域,可以看出,随着形变速率的增加,灰度值也在不断增加。
| 表 2 不同点做约束时解算的形变速率及差值/m Table 2 Deformation Rate and the Difference When Different Points as Constraint/m |
 |
 |
| 图 3 不同点做约束时的形变速率图 Figure 3 Deformation Rate Maps When Different Points as Constraint |
从图 3(a)可以看出,在仅有XJ01做约束的情况下,所画出的形变速率图与其他两个形变速率图差异较大,整幅图的形变速率基本一致,这是因为仅有一个基准,所有相干点的形变速率计算均以其为起算数据,随着相干点与GPS点距离的增加,形变速率误差也在不断增加。图 3(b)中有XJ01与XJ09两点做约束,所展示的效果较好,因为两个GPS点分布在整个网的两边,对形变速率的计算有了很好的约束,且周围有大量的InSAR相干点。图 3(c)中有XJ01、XJ09与XJ063点做约束,可以看出其与图 3(b)没有较大的区别,因为在新增加的约束XJ06周围的相干点并不多,所以该GPS点的约束能力较小,形变速率图并没有较大改变。
3 结束语本文运用西安地区相关InSAR数据与部分具有GPS数据的PS点进行实验,从实验结果中可以看出,融合过程的确对一维形变监测有明显的改正,随着GPS点数量的增加,改正效果也在不断增强,并且在GPS点分布均匀且周围有较多PS点时,改正效果更好。
本文还存在着诸多不足,如笔者在资料搜集和整理方面可能存在不足,同时因为实验区域GPS点的数量较少,在进行融合解算的过程中可选择的约束较少,且解算过程有一定误差,对融合结果有一定影响,这些在今后的研究中有待进一步改进。
| [1] | 廖明生, 林珲. 雷达干涉测量:原理与信号处理基础[M]. 北京: 测绘出版社, 2002 |
| [2] | 刘基余, 李征航, 王跃虎, 等. 全球定位系统原理及其应用[M]. 2版. 北京: 测绘出版社, 1999 |
| [3] | 许才军, 王华, 黄劲松. GPS与InSAR数据融合研究展望[J]. 武汉大学学报·信息科学版, 2003, 32(1): 58–61 |
| [4] | 许才军, 何平, 温扬茂, 等. InSAR技术及应用研究进展[J]. 测绘地理信息, 2015, 40(2): 1–9 |
| [5] | 焦明连. GPS与InSAR数据融合方法及其应用[J]. 全球定位系统, 2010, 35(3): 1–4 |
| [6] | 李振洪, 刘经南, 许才军. InSAR数据处理中的误差分析[J]. 武汉大学学报·信息科学版, 2004, 29(1): 72–76 |
| [7] | 朱武, 张勤, 丁晓利. 多参考点的PS-InSAR变形监测数据处理[J]. 测绘学报, 2012, 41(6): 886–890 |
| [8] | 胡庆东, 毛士艺. 干涉合成孔径雷达基线的估计[J]. 航空学报, 1998, 19(S1): 20–24 |
| [9] |
胡俊. 基于现代测量平差的InSAR三维形变估计理论与方法[D]. 长沙: 中南大学, 2013 |
| [10] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2003 |
| [11] | 崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 武汉: 武汉大学出版社, 2001 |
 2018, Vol. 43
2018, Vol. 43

