| 一种基于点云数据快速生成建筑物断面图的方法 |
2. 武汉大学灾害监测防治研究中心,湖北 武汉, 430079
2. Hazard Monitoring and Prevention Research Center, Wuhan University, Wuhan 430079, China
工程应用中常需要获得建筑物的断面图,传统的建筑物断面图是利用全站仪等设备采集各个独立点的三维坐标,通过软件或人工绘制成图,该方法外业工作量大,效率低且内业处理过程繁琐, 只能获得局部信息[1]。三维激光扫描是近年发展起来的一门新技术,以高精度、海量、快速、无接触测量等优势成为空间三维数据获取的有效手段[2-4],利用三维激光点云数据生成建筑物断面图,对于比较规则的断面,如地铁隧道中的区间断面等,通常按一定间隔采样来获取断面点,再对断面点进行连线并添加其他要素生成断面图。而对于比较复杂的断面,如地铁隧道变截面等,如果直接按一定间隔进行采样来获取断面点,这样生成的断面图会丢失许多重要信息,无法反映出真实的断面形状。因此,针对地铁隧道变截面等复杂断面,需要提取出断面的轮廓,考虑到该类型断面主要由呈线状分布,可首先提取出各条点云线段,然后拟合出高精度的直线参数,进而绘制变截面横断面图。点云数据中常用的直线检测方法有随机采样一致性算法[5-7]和Hough变换[8-9]。直接利用Hough变换进行点云直线检测只能达到有限精度[10],特别是受噪声影响时,如果对精度要求过高可能导致检测失败。最小二乘法[11-12]可获得均方误差意义下的精确直线,但是容易受到噪声点干扰,如果直接进行最小二乘拟合会受到强噪声干扰,达不到获取高精度直线参数的目的[13-20]。为此,本文提出了一种结合改进的Hough变换算法和选权迭代法提取建筑物轮廓线的方法,从而实现建筑物断面图快速精确绘制。
1 方法原理和实现流程基于点云数据快速生成建筑物断面图的方法其基本思想是:首先,利用地面三维激光扫描仪获取建筑物点云数据; 然后,根据需要设计一个一定范围和厚度的裁剪面(该裁剪面通常比目标断面略大,以覆盖目标断面)对目标断面进行截取,得到该断面的边缘点云数据,将此断面的边缘点云数据向XOY面投影,进而得到断面的二维点云数据; 再次,考虑到截取的边缘点云数据多呈线型分布,使用改进的Hough变换算法从边缘点云数据中提取出共线点云,对共线点云进行去噪、分割,找出点数最多的一段作为提取出第一条点云线段,将该点云线段数据从总的数据中剔除; 最后,重复以上的Hough变换提取共线点云、干扰点剔除、共线点云分割步骤提取下一条线段,直至提取出所有的线段。采用选权迭代法拟合提取出的点云线段,找出各条线段端点,对端点进行连线并添加其他要素以绘制断面图。
1.1 断面点云数据的获取该项工作的关键是如何设置一定范围和厚度的裁剪面对该建筑物断面进行截取。其方法如下。
如图 1所示,起始点A(X1, Y1, Z1), 终点B(X2, Y2, Z2)和边缘点C(X3, Y3, Z3)确定一个裁剪面ABC,AB⊥AC,由DEFG-HIJK确定一个裁剪立方体,该裁剪立方体包围目标断面,DHIE和GKJE分别表示前后平面,且与XOY平面垂直。DHKG和EIJF分别表示左右平面且同时垂直于裁剪面和前后平面,DEFG和HIJK分别表示上下平面且分别平行于裁剪面。点C为DH中点,AC长为裁剪宽度B的一半,DH长为裁剪厚度T。
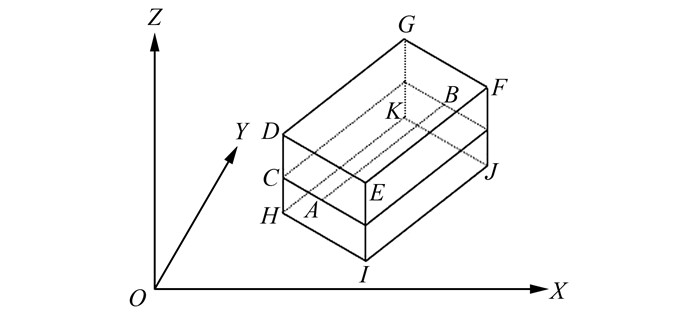 |
| 图 1 裁剪面示意图 Fig.1 A Demonstration of Cutting Surface |
已知
| $ \left\{ \begin{array}{l} \overrightarrow {AB} = \left( {{X_2} - {X_1}, {Y_{\rm{2}}} - {Y_1}, {Z_2} - {Z_1}} \right)\\ \overrightarrow {AC} = \left( {{X_3} - {X_1}, {Y_3} - {Y_1}, {Z_3} - {Z_1}} \right) \end{array} \right. $ |
则裁剪面ABC的法向量
| $ \overrightarrow n = \overrightarrow {AB} \times \overrightarrow {AC} = \left( {{X_0}, {Y_0}, {Z_0}} \right) $ | (1) |
裁剪立方体是由6个平面相交而成的实体,在计算各平面方程时规定法向量朝向立方体内部为正方向。前后平面DHIE和GKJE分别与XOY平面垂直,左右平面DHKG和EIJF指距离裁剪面起点和终点连线半个宽度,且各自平行于该连线的两个平面。上下平面DEFG和HIJK是指位于裁剪面上下半个厚度且平行于裁剪面的平面,上平面与裁剪面法向量相反,下平面与裁剪面法向量一致。分别计算出6个平面的方程。
一个空间平面的方程可表示为:
| $ Ax + By + Cz + D = 0 $ | (2) |
空间一点的坐标为(xp, yp, zp),令
| $ S = A{x_p} + B{y_p} + C{z_p} + D $ | (3) |
规定S>0表示点在正面,S=0表示点平面上,S < 0表示点在背面。将待截取范围内的点云数据逐个代入6个平面的方程中,当点都在6个平面的正方向时,认为该点是要截取的点,存储下来继续计算下一点,直至计算完毕,将此断面的边缘点云数据向XOY面投影,得到断面的二维点云数据Poriginal,从而实现建筑物断面点云数据的获取。
1.2 共线点云的提取在获得断面边缘点云的二维平面数据Poriginal后,需要提取出每条点云线段,本文选择Hough变换算法进行提取。Hough变换的实现是一种投票过程:先将参数平面按一定步长离散化为许多小格; 然后,采用“多对一”映射,计算空间中共线的多个点在参数平面中对应的参数值,若计算结果落在参数平面某一小格内,就使该小格的累加器加1,累积值最大的小格即为空间中直线的参数,把检测到的点从总的数据中剔除; 最后, 进入下一循环继续检测,直到检测出所有直线为止。不同于图像的原点坐标一般在图像边缘,隧道点云数据坐标通常距离原点较远,如果直接进行Hough变化将占用大量内存,大大增加处理时间,有时会超出计算机的处理能力导致崩溃,又由于Hough变换过程中计算极径时需要向上取整,势必会产生较大的误差,这样无法分别出差别较小的直线,因此,在Hough变换之前需要对点云数据进行适当的平移和放大。具体的变换过程如下:
1) 对二维点云集合Poriginal, 先计算出中心位置(Xm,Ym),将点云数据整体平移,使其中心与原点重合,再将点云坐标整体放大1 000倍(作用是在投票过程中精确到小数点后3位,可根据实际情况进行调整),利用转换后坐标算出向上取整后的极径最大值ρmax。
2) 设置两个m×n累加器矩阵,m为将180°等分的个数,n为步骤1)中ρmax取整数。计算每个θi下对应的所有点向上取整后的极径ρij = xjcosθi+ yjsinθi,其中1≤j≤N,N为集合Poriginal点数, 找到θi和ρij所对应的单元,并将该单元的累加器加1。由于平移后计算出的极径值有时为负,所以需要设置两个累加器矩阵。
3) 找出步骤2)中两个累加器中值最大的单元,其所对应的θmax和ρmax即为极坐标系中的角度和极径。设置一个阈值t1,逐点计算角度θmax下点云对应的极径值ρj= xjcosθmax+yjsinθmax(1≤j≤N, N为集合Poriginal点数),如果- t1≤ρj-ρmax≤t1,认为点在该条直线上, 将其存储起来继续计算下一点, 直至计算完毕提取出一条共线点云集合Pline。
1.3 干扰点的剔除在使用Hough变化提取共线点云集合Pline的过程中,由于对极径值ρj设定了阈值t1,相当于对共线点云设置了一定厚度,那么就不可避免地掺杂干扰点,特别集中在两端与其他线段连接处,如果直接进行最小二乘拟合会受到干扰点影响,达不到获取高精度直线参数的目的。而Hough变换对噪声不敏感,基于这一性质,利用前面得到的θmax和ρmax去除部分噪声点,原理如下。
集合Pline所在直线的斜截式方程为:
| $ {y_i} = {a_k}{x_i} + {b_k} $ | (4) |
式中,
逐点计算Pline中点到式(4)确定直线的距离为:
| $ {d_i} = \frac{{\left| {{a_k}{x_i} + {b_k} - {y_i}} \right|}}{{\sqrt {1 + a_k^2} }} $ | (5) |
式中,(xi, yi)∈Pline。
设定一个阈值t2作为点到直线的最远距离(0<t2<t1),如果di≤t2,则有:
| $ \left( {{x_i}, {y_i}} \right) \in {P_{{\rm{denoising}}}} $ | (6) |
将距离直线不大于t2的点存储在Pdenoising中,该过程可有效去除线段连接处的干扰点。
1.4 共线点云的分割集合Pdenoising目前仍旧是一些共线点云,需要对其进行排序和分割,找出点数最多的一段。
1) 利用Hough变换中得到的直线角度θmax对Pdenoising坐标进行排序,如果0°≤θmax≤45°或145°≤θmax<180°, 将x坐标从小到大进行排序,y坐标随之变化; 如果45°<θmax<145°,则将y坐标从小到大进行排序,x坐标随之变化。
2) 逐点计算排序后的两点之间距离Li,设定一个阈值t3作为相邻两点间的最远距离,如果Li≤t3,认为两点在一条线段上,继续计算下一点,如果Li>t3,认为该点与前面点不在一条线段上,把前面点存在一个数组中,从该点继续计算,直到将共线点云分割完毕。
3) 比较步骤2)中分割后各条点云线段的点数,取点数最多的一段作为提取出的第一条点云线段集合Psegment。
4) 将Psegment从集合Poriginal中删除,重复以上的共线点云提取、干扰点剔除、共线点云分割步骤,提取下一条点云线段。设定一个阈值t4作为点云线段的最少点数,当点云线段的点数小于t4时结束循环。至此提取出全部的点云线段。
1.5 点云线段的拟合提取出点云线段后,要想得各条轮廓线最终出图使用,还需对点云线段数据进行分段拟合,由于点云数据量一般较大,又提取出的Psegment已按坐标排好序,可按一定间隔抽稀得到Psubsampling,不仅不会改变其形状,由于数据量的减少还会加快拟合速度。接下来设定一个长度阈值t5,用于对过长的线段进行分割,首先计算Psubsampling点云线段的长度Ls,如果Ls>t5,则以t5为尺度将Ls分成若干段,再对每一小段采用选权迭代法进行精确直线拟合,定权时采用丹麦权,其作用是对中误差过大的点进行降权,以降低其对平差结果的影响,丹麦权有很多形式,这里采用如下一种:
| $ \left\{ \begin{array}{l} v_{{y_i}}^2 = 1, \left| {{v_{{y_i}}}} \right| < 1.5\sigma \\ v_{{y_i}}^2 = v_{{y_i}}^2{e^{1 - }}{\left( {\frac{{v_{{y_i}}^2}}{{1.5\sigma }}} \right)^2}, \left| {{v_{{y_i}}}} \right| \ge 1.5\sigma \\ v_{{y_i}}^2 = 0, \left| {{v_{{y_i}}}} \right| > 5\sigma \end{array} \right. $ | (7) |
如果线段角度小于45°或大于145°,对x和y坐标采用最小二乘法拟合出直线方程,利用两端点的x坐标,代入直线方程求出y坐标; 如果线段角度大于45°且小于145°,对y和x坐标采用最小二乘法拟合出直线方程,利用两端点的y坐标,代入直线方程求出x坐标,最后将得到的端点坐标再平移缩放回去即可。
1.6 断面图的生成求得各条线段的端点坐标后,将其首尾相连,添加内外图廓、站名、单位、测量者、绘制者、检查者等信息, 即可得到相应的断面图。
2 算法实现与工程应用分析为了考察本文提出的基于点云数据快速生成建筑物断面图方法的可行性,编程实现了该方法。并用于武汉地铁2号线一段变截面的横断面测量中。
2.1 算法实现程序设计和调试时,参数大小的选取非常关键。设置累加器矩阵为900×1 000Rmax,即将180°划分成900份,找出中心位置(Xm,Ym),将点云数据整体平移,使其中心与原点重合,再将点云坐标整体放大1 000倍。阈值t1取0.03 m,阈值t2取0.015 m,阈值t3取0.15 m,阈值t4取20,阈值t5取0.5 m,因坐标放大了1 000倍,t1、t2、t3和t5也应放大相应倍数。
2.2 工程应用采用徕卡ScanStation P30三维激光扫描仪对武汉地铁2号线的一段隧道进行分段扫描获取点云数据,然后取一个与隧道设计中心线平行的裁剪面,该裁剪面宽度为15 m(比隧道宽度略大),厚度为0.02 m,长度比变截面要略长,使变截面在该裁剪面之内。图 2给出了截取变截面示意图, 包围了整个变截面,利用本文介绍的方法获取该部分的横断面点云数据,共获得73 272个点。图 3(a)给出了截取的变截面横断面边缘点云数据的平面效果图,可以看出,它与原始变截面轮廓相对应。
 |
| 图 2 截取变截面示意图 Fig.2 Variable Section Interception |
 |
| 图 3 变截面断面线提取 Fig.3 Variable Section Line Extraction |
通过改进的Hough变换算法提取共线点云数据,并经过干扰点的剔除,共线点云的分割得到各条点云线段,为方便区分,对各条点云线段设置了不同的颜色。其结果如图 3(b)所示。经过点云线段的精确拟合,找出各条线段端点,对端点进行连线绘制地铁隧道变截面横断面图,如图 3(c)所示。
由图 3(c)可以看出,成功提取出了大部分线段,各条线段之间的界限清晰,而且自动生成的隧道变截面纵断面图与图 3(a)轮廓相对应,说明该算法既利用了Hough变换在直线提取领域的优势,又有效解决了Hough变换提取直线时精度不够的问题,同时该算法也兼顾了处理效率。如果直接采用最小二乘进行直线拟合,时间约为2 min,但这样会导致部分线段由于受噪声点的影响而拟合不精确,因此为抵抗噪声点的干扰,本文采用选权迭代法进行直线拟合,拟合过程中对点云线段适当做了抽稀处理,从提取点云线段数据到直线拟合全过程约为20 min。
中间过程中干扰点剔除步骤效果如图 4(a)和图 4(b)所示,为方便分析,选取断面的左下角部分进行局部放大,可以看出,由于对极径设定了阈值0.03 m,相当于对共线点云设置了一定厚度,那么在两端与其他线段连接处就不可避免掺杂干扰点,经过干扰点剔除处理后有效去除了部分干扰点,如此可提高直线拟合及提取端点坐标时的精度。
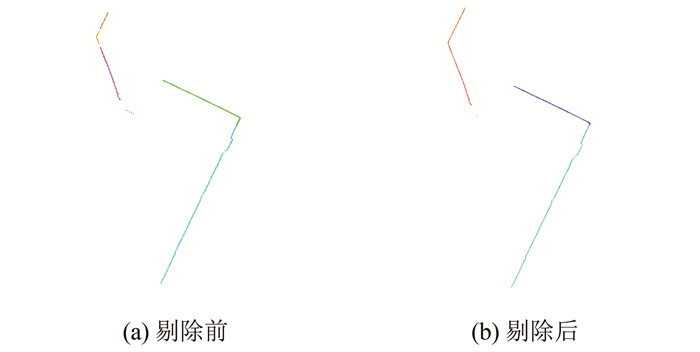 |
| 图 4 干扰点剔除 Fig.4 Noise Point Elimination |
为了进一步考察断面图生成效果,将图 3(c)与图 3(a)进行叠加显示,如图 5所示,为了能清楚地显示效果,图 5(a)、5(c)分别为全局图(图 5(b))的左下角和右下角部分局部放大显示图。
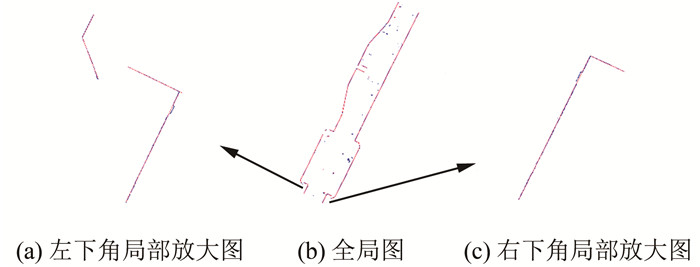 |
| 图 5 叠加显示图 Fig.5 Overlay Chart |
由图 5可以看出, 直线拟合时采用的选权迭代算法具有良好的抗差效果,有效地消除了噪声点的干扰,拟合的直线与原始点云吻合良好。
将该断面图编辑后与其他规则断面进行拼接,添加图廓、站名、单位、测量者、绘制者等信息, 即可得到地铁隧道横断面竣工图,如图 6所示。
 |
| 图 6 地铁隧道横断面图 Fig.6 Subway Tunnel Cross Section |
3 结束语
利用三维激光点云数据,结合改进的Hough变换算法和基于选权迭代的最小二乘法等技术提取建筑物某一断面点云数据进而生成断面图方法,结合工程实例验证了该方法的可靠性和实用性,是一种高效的实现建筑物断面图快速绘制手段。考虑到建筑物形式多种多样,目前该方法主要提取直线要素,后期还可根据需要编程实现圆形、椭圆及其他曲线的提取。
| [1] |
高益健, 高俊强, 赵亚萍. 利用徕卡全站仪机载程序进行隧道断面测量[J]. 测绘工程, 2014, 23(11): 71-73. DOI:10.3969/j.issn.1006-7949.2014.11.016 |
| [2] |
唐琨, 花向红, 魏成, 等. 基于三维激光扫描的建筑物变形监测方法研究[J]. 测绘地理信息, 2013, 38(2): 54-55. |
| [3] |
张荣华, 李俊峰, 林昀. 三维激光扫描技术在土方量算中的应用研究[J]. 测绘地理信息, 2014, 39(6): 47-49. |
| [4] |
艾卫涛.三维激光扫描点云去噪及在建模中的应用[D].西安: 西安科技大学, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10704-1017725587.htm
|
| [5] |
Schnabel R, Wahl R, Klein R. Efficient RANSAC for Point Cloud Shape Detection[J]. Computer Graphics Forum, 2007, 26(2): 214-226. |
| [6] |
Fischler M A, Bolles R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 2011, 24: 381-395. |
| [7] |
Chen D P, Chu X N, Sun X W, et al. A New Product Service System Concept Evaluation Approach Based on Information Axiom in a Fuzzy-Stochastic Environment[J]. International Journal of Computer Integrated Manufacturing, 2015, 28(11): 1123-1141. |
| [8] |
王竞雪, 朱庆, 王伟玺, 等. 结合边缘编组的Hough变换直线提取[J]. 遥感学报, 2014, 18(2): 384-389. |
| [9] |
Camurri M, Vezzani R, Cucchiara R. 3D Hough Transform for Sphere Recognition on Point Clouds[J]. Machine Vision and Applications, 2014, 25(7): 1877-1891. DOI:10.1007/s00138-014-0640-3 |
| [10] |
张采芳, 田岩, 郑毓勇. 基于最优尺度的高分辨率遥感影像道路提取[J]. 测绘通报, 2015(1): 90-94. |
| [11] |
郭斯羽, 翟文娟, 唐求, 等. 结合Hough变换与改进最小二乘法的直线检测[J]. 计算机科学, 2012, 39(4): 196-200. DOI:10.3969/j.issn.1002-137X.2012.04.045 |
| [12] |
邱卫宁, 陶本藻, 姚宜斌, 等. 测量数据处理理论与方法[M]. 武汉: 武汉大学出版社, 2008.
|
| [13] |
马洪滨, 何群, 邵永东, 等. 基于最小二乘的选权迭代抗差拟合模型研究[J]. 沈阳建筑大学学报(自然科学版), 2007, 23(5): 768-771. DOI:10.3969/j.issn.2095-1922.2007.05.015 |
| [14] |
陈盖凯. 基于Hough变换的直线检测[J]. 西安航空技术高等专科学校学报, 2007, 25(3): 34-36. DOI:10.3969/j.issn.1008-9233.2007.03.012 |
| [15] |
张吉玲. 基于Hough变换检测直线的研究[J]. 福建电脑, 2009, 25(4): 89-90. DOI:10.3969/j.issn.1673-2782.2009.04.059 |
| [16] |
朱芳芳, 顾宏斌, 孙瑾. 一种改进的Hough变换直线检测算法[J]. 计算机技术与发展, 2009, 19(5): 19-22. DOI:10.3969/j.issn.1673-629X.2009.05.006 |
| [17] |
李慧鹏, 朱伟伟, 谭朦曦, 等. 基于改进Hough变换的直线检测算法[J]. 半导体光电, 2017, 38(4): 603-608. |
| [18] |
乔寅骐, 肖健华, 黄银和, 等. 基于最小二乘修正的随机Hough变换直线检测[J]. 计算机应用, 2015, 35(11): 3312-3315. |
| [19] |
祁宝英. 运用Hough变换提高直线检测效率[J]. 计算机系统应用, 2012, 21(6): 228-231. DOI:10.3969/j.issn.1003-3254.2012.06.053 |
| [20] |
杨勇喜, 贾东振, 何秀凤. 基于选权迭代法的抗差整体最小二乘及其应用[J]. 测绘工程, 2014, 23(12): 56-59. DOI:10.3969/j.issn.1006-7949.2014.12.014 |
 2020, Vol. 45
2020, Vol. 45


