| 基于小波抗混叠单子带重构改进算法的测量信号特征提取 |
2. 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都, 610031;
3. 成都翰诚科技有限公司,四川 成都,610031
2. State-Province Joint Engineering Laboratory of Spatial Information Technology for High-Speed Railway Safety, Chengdu 610031, China;
3. Chengdu Hancheng Technology Co., Ltd., Chengdu 610031, China
随着测量技术自动化水平的不断提高,越来越多的工程使用各类型的传感器进行自动实时测量,这些测量信号中包含许多非平稳的噪声信号,而小波分析是能够有效分析此类信号的时频分析方法[1]。
Mallat算法是离散小波变换的快速算法,该算法使用滤波器H、h、G、g对信号进行分解和重构,其中,H、h分别是分解和重构时的低通滤波器,G、g分别是分解和重构时的高通滤波器[2]。首先,用单子带重构算法将信号按Mallat算法进行分解,得到各尺度上的小波系数;然后,将各子带上的小波系数分别重构至原始信号相同的尺度[3]。通过对重构好的信号作快速傅里叶变换,可以直观地得到各子带上包含的频率信息,为提取分析测量信号的特征频率信息提供依据[4]。
传统的单子带重构算法在某些频段会发生幅值失真和频率混叠,出现虚假信号的现象[5],实际应用中可能会提取出错误的特征频率信息,并且测量信号的成分越复杂,单子带重构算法提取出错误特征信息的可能性越大,就越不利于对测量信号的分析处理。因此,杨建国[3]提出了单子带重构改进算法,在原来算法的基础上加入了纠正滤波器对各子带信号进行的处理,基本上消除了Mallat算法中的频率混淆问题,但重构结果中依然存在频率混淆的现象[6]。小波抗混叠单子带重构改进算法又在单子带重构改进算法的基础上,多加入了一个纠正滤波器和去掉暂态过程点的步骤,不仅消除了频率混淆的问题,还解决了测量信号与滤波器卷积后信号长度改变的问题。
1 小波抗混叠单子带重构改进算法的提出 1.1 Mallat算法和单子带重构改进算法的频率混淆Mallat算法主要是由与小波滤波器卷积、隔点采样和隔点插零3个要素组成,该算法由分解算法和重构算法组成[3]。信号经分解后,各子带的频率范围与原始信号f(t)的采样频率2fs存在如表 1所示的关系。其中,Aj为信号在第j层的近似或低频部分的小波系数;Dj为信号在第j层的细节或高频部分的小波系数;J表示的是第J层的系数,j的取值为[1, J]。
| 表 1 Mallat算法中各子带的频率范围 Tab.1 Frequency Aange of Sub-bands in Mallat Algorithm |
 |
由表 1可知,利用Mallat算法对信号进行分解而得到的第j+1层的低频部分是第j层低频部分的低半频带,第j+1层的高频部分是第j层低频部分的高半频带[3]。而每一层高频部分子带所包含的频率成分与该子带所对应的采样频率都违反了采样定理,因此,Mallat算法本身存在比较严重的频率混淆现象[7]。
在Mallat算法中,隔点采样和隔点插零两个过程都存在频率混淆现象,且两者的频率混淆具有反向折叠的作用,消除了由于上下采样引起的频率折叠[8],即在信号分解时出现的频率混淆在重构时被纠正了,利用Mallat算法得到的小波系数能够精确地重构原始信号。但在使用Mallat算法提取复杂测量信号的某些频率成分或某一频段的信号分量时,不能忽视Mallat算法存在的频率混淆问题。因此,提出了单子带重构算法,由于单子带重构算法中使用的实际滤波器的非理想截止特性,它和Mallat算法一样都必然存在频率混淆现象[9]。
单子带重构改进算法是在单子带重构算法的基础上加入了不同的纠正滤波器,利用快速傅里叶变换及其逆变换去掉子带中多余的频率成分,以避免或减少重构的信号中存在的频率混淆现象,其算法如图 1所示。
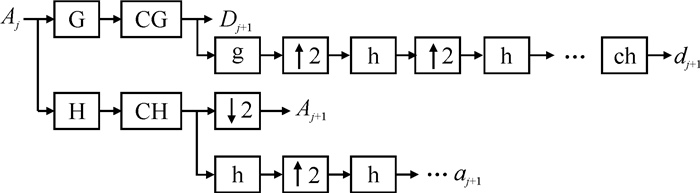 |
| 图 1 单子带重构改进算法图 Fig.1 Improved Single Sub-band Reconstruction Algorithm |
图 1中,
| $ \left\{ \begin{array}{l} X(k) = \sum\limits_{n = 0}^{{N_j} - 1} {x(n), 0 \le k \le \frac{{{N_j}}}{4}或\frac{{3{N_j}}}{4} \le k \le {N_j}} \\ X(k) = 0, k取其他值时 \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} X(k) = \sum\limits_{n = 0}^{{N_j} - 1} {x(n){W^{kn}}, \frac{{{N_j}}}{4} \le k \le \frac{{3{N_j}}}{4}} \\ X(k) = 0, k取其他值时 \end{array} \right. $ | (2) |
单子带重构改进算法基本消除了Mallat算法中的频率混淆,但最后重构的结果中依然存在少量频率混淆的现象,其原因在于该算法的纠正滤波器不能完全消除由于小波滤波器的非理想截止特性而产生的多余频率分量。
1.2 小波抗混叠单子带重构改进算法小波抗混叠单子带重构改进算法针对单子带重构改进算法出现的问题,在其基础上增加了一个纠正滤波器和去暂态过程点的步骤,一方面解决了单子带重构改进算法没有完全消除频率混淆的问题;另一方面解决了由于和小波滤波器卷积而导致的测量信号变换前后长度不一致的问题。其具体算法如图 2所示。
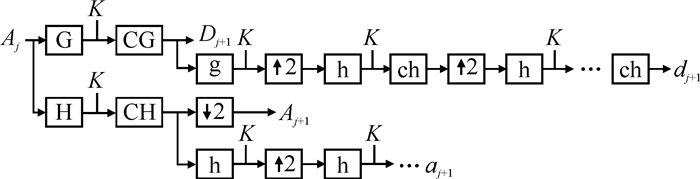 |
| 图 2 小波抗混叠单子带重构改进算法图 Fig.2 Improved Anti-aliasing Single Sub-band Reconstruction Algorithm |
该算法在细节信号重构时,在第一个低通重构滤波器和隔点采样之间加入一个纠正滤波器
假设一个仿真信号y:
| $ \begin{array}{l} y = \sin (40\pi t) + \sin (60\pi t) + \sin (90\pi t) + \\ \sin (150\pi t) + \sin (180\pi t) + {e^{ - 30t}}\sin (320\pi t) \end{array} $ | (3) |
信号y中包含20 Hz、30 Hz、45 Hz、75 Hz、90 Hz和160 Hz共6个频率成分,其中,160 Hz的频率成分为一瞬态信号分量,分别发生在0.5 s和0.95 s两个时刻。信号y的时间波形及其频谱如图 3(a)所示,其频谱放大如图 3(b)所示。
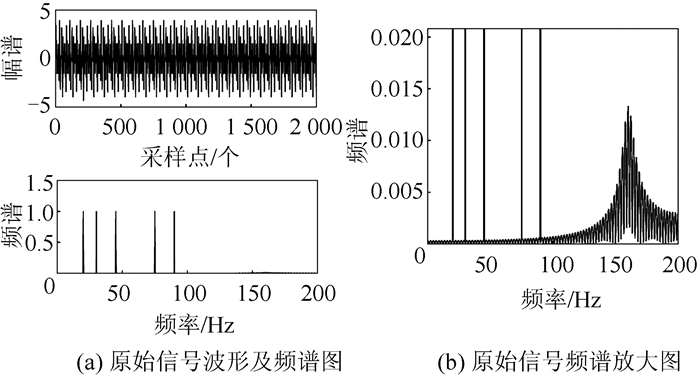 |
| 图 3 信号y的时间波形和频谱 Fig.3 Time Waveform and Spectrum of Signal y |
分别用单子带重构算法、单子带重构改进算法和抗混叠单子带重构改进算法对信号y进行处理,以400 Hz采样频率采取2 000个点,选用sym5小波对y进行尺度J=3的分解重构。理论上各子带的频率结果如表 2所示。
| 表 2 信号y按Mallat算法分解的频率成分理论结果/Hz Tab.2 Frequency Theoretical Results of Signal y with Mallat Algorithm/Hz |
 |
图 4是利用单子带重构算法对信号y进行分解重构得到的结果及其各子带的频谱图。
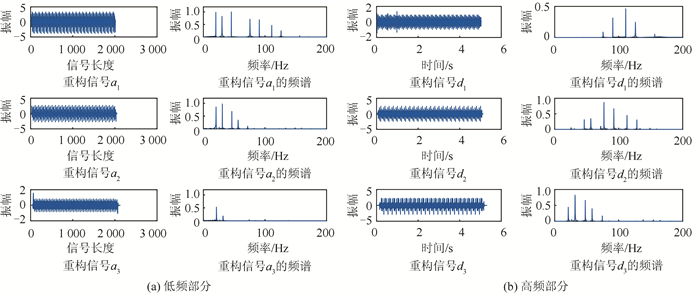 |
| 图 4 单子带重构算法分析的结果 Fig.4 Result of Single Sub-band Reconstruction Algorithm |
由图 4可知,利用该算法得到低频和高频子带部分都存在严重的频率混淆,且不能明显检测出160 Hz的瞬态信号,并且重构出的第1层、第2层、第3层的数据长度分别是2 018、2 054和2 126,与原始数据长度不一致。
图 5是利用单子带重构改进算法对信号y进行分解重构得到的结果及其各子带的频谱图。
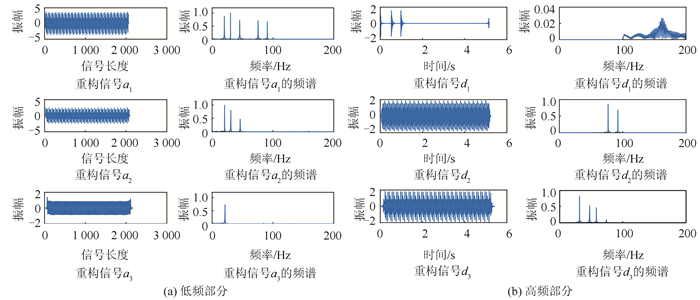 |
| 图 5 单子带重构改进算法分析得到的结果 Fig.5 Result of Improved Single Sub-band Reconstruction Algorithm |
由图 5可知,利用该算法得到低频子带及高频子带第1层和第2层部分均消除了频率混淆,明显检测出0.5 s和0.95 s两个时刻的频率为160 Hz的瞬态信号,但高频子带第3层部分仍然存在频率混淆的现象,而重构出的第1层、第2层、第3层的数据长度分别是2 018、2 054和2 126,与原始数据长度不一致,从重构数据a3、d1可以明显看出边界效应的问题。
图 6是利用抗混叠单子带重构改进算法对信号y进行分解重构得到的结果及其各子带的频谱图。
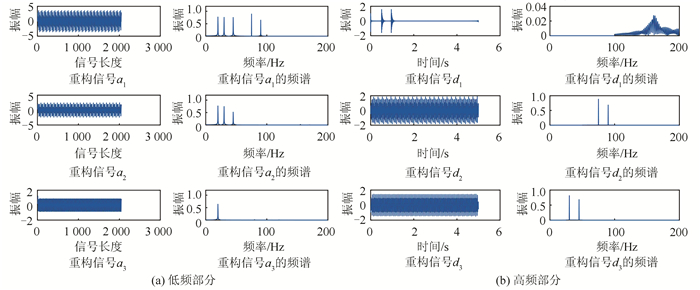 |
| 图 6 抗混叠单子带重构改进算法分析得到的结果 Fig.6 Result of Improved Anti-aliasing Single Sub-band Reconstruction Algorithm |
由图 6可知,利用该算法得到的低频子带及高频子带部分与理论结果完全一致,有效地消除了频率混淆,精确地检测到了0.5 s和0.95 s两个时刻的瞬态信号。并且,通过卷积后去掉表示暂态过程点的步骤,保证了每一子带的重构数据长度均与原始仿真数据一致,消除了边界效应问题。
3 结束语单子带重构改进算法不能完全消除Mallat算法中存在的频率混淆,在提取测量信号特征信息时可能得到错误的结果,小波抗混叠单子带重构算法利用纠正滤波器能够完全抑制Mallat算法中频率混淆现象,并使用去暂态过程点这一步骤解决了每一子带重构后的信号与原始信号长度不一致的问题。仿真信号的计算证明了该方法的有效性,说明小波抗混叠单子带重构改进算法在各种测量信号特征提取分析方面都有较好的应用前景。
| [1] |
孙宽雷, 韩峻. 基于单子带重构改进算法的舰炮自动机故障特征提取方法[J]. 舰船电子工程, 2014, 34(10): 123-126. |
| [2] |
Qin Y, Wang J X, Tang B P, et al. Higher Density Wavelet Frames with Symmetric Low-Pass and Band-Pass Filters[J]. Signal Processing, 2010, 90(12): 3 219-3 231. DOI:10.1016/j.sigpro.2010.05.027 |
| [3] |
杨建国. 小波分析及其工程应用[M]. 北京: 机械工业出版社, 2005.
|
| [4] |
胡耀斌, 谢静, 胡良斌. 基于神经网络与小波变换的滚动轴承故障诊断[J]. 机械设计与研究, 2013, 29(6): 33-35. DOI:10.3969/j.issn.1006-2343.2013.06.009 |
| [5] |
李辉, 丁桦. 一种抗混叠和失真的小波包信号分解与重构算法[J]. 科学技术与工程, 2008(20): 5 580-5 588. |
| [6] |
王林.小波抗混叠单子带重构算法及其在轴承故障特征提取中的应用[D].重庆: 重庆大学, 2012
|
| [7] |
许珉, 程兴民. 基于单子带重构改进小波变换的电力系统谐波检测方法[J]. 电力自动化设备, 2008(9): 10-14. DOI:10.3969/j.issn.1006-6047.2008.09.003 |
| [8] |
卢鑫, 袁兴明. 基于M带小波的GPS信号特征提取探测[J]. 山东理工大学学报(自然科学版), 2011, 25(4): 45-48. DOI:10.3969/j.issn.1672-6197.2011.04.010 |
| [9] |
邵克勇, 蔡苗苗, 李鑫. 基于小波分析及奇异值差分谱理论的滚动轴承故障诊断[J]. 制造业自动化, 2013, 35(8): 79-82. DOI:10.3969/j.issn.1009-0134.2013.08.023 |
 2019, Vol. 44
2019, Vol. 44

