| 改进的新陈代谢GM(1, 1)模型在建筑物沉降预测中的应用 |
2. 武汉大学灾害监测和防治研究中心, 湖北 武汉, 430079
2. Hazard Monitoring and Prevention Research Center, Wuhan University, Wuhan 430079, China
灰色模型具有能够利用少数据进行预测的优点。灰色模型有很多种,其中用于沉降预测的主要有GM(1,1)模型[1]、新陈代谢GM(1,1)模型[2, 3]等。实际上任何灰色系统随着时间的推移,都会不断有随机的驱动或扰动因素进入系统并且影响系统的发展。而新陈代谢模型注重的是在不断补充新数据的同时去掉旧数据,从而更好地体现出系统的发展趋势,获得更精确的预测结果。相比之下,新陈代谢GM(1,1)模型的实用性会更高一些[4],这是新陈代谢GM(1,1)模型的一大优点。新陈代谢GM(1,1)模型的预测方程与GM(1,1)模型一样,模型预测值也会出现误差累积,而且模型在处理一些具有较大变动幅度的数据时存在失真问题,使预测值出现偏离,大大降低模型的预测精度[5, 6]。因此,本文采用了一种新的预测方案,即不再定义灰色微分方程或白化方程,直接通过一次累加生成,然后累减还原得出灰色预测的代数递推方程[5],这样使得预测结果仅与序列的初始值有关,提高了模型的预测精度,从而解决了新陈代谢GM(1,1)模型的预测失真问题。在此基础上,以长江紫都3期沉降监测2号点的沉降资料为例, 利用改进前后的新陈代谢GM(1,1)模型进行了分析。
1 改进的新陈代谢GM(1, 1)模型 1.1 新陈代谢GM(1, 1)模型新陈代谢GM(1,1)模型是灰色模型中的一种, 并且是GM(1,1)模型群中最理想的模型。相对于传统GM(1,1)模型而言[1],新陈代谢GM(1,1)模型能够更好地反映建筑物沉降的发展趋势[7]。
传统GM(1,1)模型原理:给定原始非负时间序列X(0)={X(0)(1), X(0)(2), X(0)(3), …, X(0)(n)},其中n为定参数据长度,式中的数据多为无规律的、随机的, 通过累加生成的新序列可弱化原始数据的随机性。累加生成后的新序列为X(1)={X(1)(1), X(1)(2), X(1)(3), …, X(1)(n)},其中:
| $ {X^{(1)}}(t) = \sum\limits_{i = 1}^t {{X^{(0)}}} (i),t = 2,3, \cdots ,n $ | (1) |
式中, t表示定参数据期数。原始序列与新序列之间满足:
| $ {X^{(0)}}(t) + m{X^{(1)}}(t) = n $ | (2) |
式中, 方程是GM(1,1)模型的原始形式,也被称作灰色微分方程。
对累加生成的新序列做紧邻生成:
| $ \begin{array}{*{20}{c}} {{z^{(1)}}(t) = 1/2\left[ {{X^{(1)}}(t - 1) + {X^{(1)}}(t)} \right],}\\ {t = 2,3, \cdots ,n} \end{array} $ | (3) |
则GM(1,1)模型的基本形式为:
| $ {X^{(0)}}(t) + a{z^{(1)}}(t) = u $ | (4) |
运用最小二乘法对式(4)进行参数估计,求解参数a和u,得到:
| $ \mathit{\boldsymbol{A}} = {[a,u]^{\rm{T}}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{Y}}_n} $ | (5) |
式中,
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - 1/2\left[ {{X^{(1)}}(1) + {X^{(1)}}(2)} \right]}&1\\ { - 1/2\left[ {{X^{(1)}}(2) + {X^{(1)}}(3)} \right]}&1\\ \vdots & \vdots \\ { - 1/2\left[ {{X^{(1)}}(n - 1) + {X^{(1)}}(n)} \right]}&1 \end{array}} \right]\\ {\mathit{\boldsymbol{Y}}_n} = \left[ {{X^{(0)}}(2),{X^{(0)}}(3), \cdots ,{X^{(0)}}(n)} \right] \end{array} \right. $ | (6) |
GM(1,1)模型的一阶一元微分方程为:
| $ \frac{{{\rm{d}}{X^{(1)}}}}{{{\rm{d}}t}} + a{X^{(1)}} = u $ | (7) |
利用式(7)和初始条件X(1)(1)=X(0)(1),可以求出X(1)(t)为:
| $ {X^{(1)}}(t) = \left[ {{X^{(0)}}(t) - \frac{u}{a}} \right]{{\rm{e}}^{ - a(t - 1)}} + \frac{u}{a} $ | (8) |
改写累加公式X(1)={X(1)(1), X(1)(2), X(1)(3), …, X(1)(n)}为:
| $ \begin{array}{*{20}{c}} {{X^{(1)}}(t) = \sum\limits_{i = 1}^{t - 1} {{X^{(0)}}} (i) + {X^{(0)}}(t) = }\\ {{X^{(1)}}(t - 1) + {X^{(0)}}(t)} \end{array} $ | (9) |
经过一次累减还原,即得到X(0)(t)序列:
| $ {X^{(0)}}(t) = {X^{(1)}}(t) - {X^{(1)}}(t - 1) $ | (10) |
以上就是传统GM(1,1)模型的预测过程。用新陈代谢模型进行预测时的不同点在于:首先,由原始数据序列建立GM(1,1)模型并且求出预测值X(0)(n+1);然后,在原始数据序列中置入新求得的数据X(0)(n+1), 同时去掉最老信息X(0)(1), 形成新序列{X(0)(2), X(0)(3), …, X(0)(n),X(0)(n+1)},再次建立GM(1,1)模型, 如此反复依次递补, 直到完成预测目标, 即为新陈代谢GM(1,1)模型[8]。
1.2 新陈代谢GM(1, 1)模型的改进合并式(3)和式(4)可以得到:
| $ {X^{(0)}}(t) + a/2\left[ {{X^{(1)}}(t - 1) + {X^{(1)}}(t)} \right] = u $ | (11) |
将式(10)代入式(11)可以得到:
| $ (1 + a/2){X^{(0)}}(t) + a{X^{(1)}}(t - 1) = u $ | (12) |
再将式(8)代入式(12), 可以得到新的灰色预测迭代方程为:
| $ {X^{(0)}}(n) = \frac{{2{{(2 - a)}^{n - 2}}}}{{{{(a + 2)}^{n - 1}}}}\left( { - a{X^{(0)}}(1) + u} \right) $ | (13) |
式中, 采用了新的代数递推方程替代原始的灰色微分方程或白化方程,使得预测值的结果仅与X(0)(1)相关,避免了误差累积,提高了预测精度,在处理具有较大变动幅度的数据时效果更明显。在进行测量时,直接用式(13)的方程求解预测值,即为新陈代谢模型的改进。
1.3 模型精度检验1) 模型残差为:
| $ \varepsilon (i) = {{\hat X}^{(0)}}(i) - {X^{(0)}}(i),i = 1,2,3, \cdots $ | (14) |
式中,
2) 序列X(0)(t)的均值和方差为:
| $ \left\{ {\begin{array}{*{20}{l}} {\bar X = \sum\limits_{i = 1}^n {{X^{(0)}}} (i)/n}\\ {S_1^2 = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{X^{(0)}}(i) - \bar X} \right)}^2}} } \end{array}} \right. $ | (15) |
3) 残差ε(i)的均值和方差为:
| $ \left\{ {\begin{array}{*{20}{l}} {\bar \varepsilon = \sum\limits_{i = 1}^n {{\varepsilon ^{(0)}}} (i)/n}\\ {S_2^2 = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{\varepsilon ^{(0)}}(i) - \bar \varepsilon } \right)}^2}} } \end{array}} \right. $ | (16) |
4) 后验方差比为C=S2/S1。
5)
| 表 1 模型预测精度分级 Tab.1 Model Predictive Precision Rating |
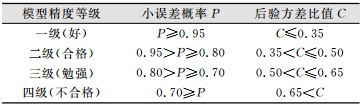 |
2 工程应用和结果分析 2.1 原始数据
为了考查改进模型的可行性,本文以长江紫都3期沉降监测2号点的沉降资料为例进行了实验与分析。为了确保施工期间建筑物安全性及质量的可控性,需要对建筑物以及地下设施进行沉降监测。2号点观测数据详如表 2所示,从数据可以看出,第8期~第17期的数据变动幅度比较大,所以本文选取了第9期~第16期的数据进行了实验与分析。
| 表 2 2号点观测数据 Tab.2 Observation Data of No.2 |
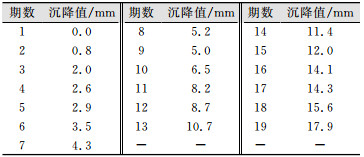 |
2.2 模型预测计算
首先,本文选用第3期~第8期数据{2, 2.6, 2.9, 3.5, 4.3, 5.2}作为原始时间数据序列建立模型,求出第9期的预测值6 mm;然后,在原始时间序列中使用第9期的预测值作为新的数据,并去掉第3期的观测数据,构建新的时间数据序列{2.6, 2.9, 3.5, 4.3, 5.2,6};重复上述步骤预测第10期的观测值, 逐步循环, 直到得出第16期的观测值;最后,再用改进的新陈代谢模型重复上述方法进行预测,结果如表 3所示。
| 表 3 预测结果对比 Tab.3 Prediction Results Comparison |
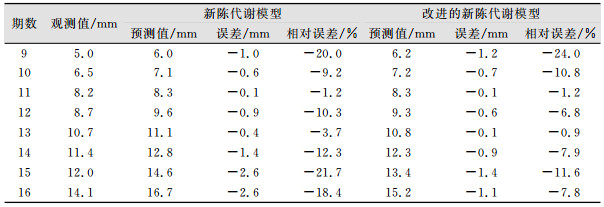 |
2.3 精度检验与分析
从表 3的预测值中可以看出,随着时间间隔变长,新陈代谢GM(1,1)模型的预测误差逐渐增大,而相比之下改进模型的预测值仍保持着较高的精度。新陈代谢和改进的新陈代谢模型精度对比如表 4所示。从表 4可以看出,两个模型的精度等级均为一级,但是通过对平均相对误差和均方差比值两个指标的对比可以看出,改进后的模型预测精度明显高于新陈代谢GM(1,1)模型的预测精度。
| 表 4 两种模型精度对比 Tab.4 Accuracy Comparison of Two Models |
 |
3 结束语
本文在研究建筑物的沉降预测时,对新陈代谢GM(1,1)模型做了改进,并在此基础上以长江紫都3期的沉降数据为例,利用改进后的模型与新陈代谢模型进行实验分析。结果表明,改进后的模型不仅继承了新陈代谢模型原有的特点,还明显提高了预测精度,避免了预测失真问题,说明改进后的新陈代谢GM(1,1)模型切实可行。
| [1] |
高宁, 崔希民, 高彩云. 高层建筑物沉降变形的灰线性预测[J]. 测绘科学, 2012, 37(3): 96-98. |
| [2] |
翟信德, 高飞, 徐文兵. 新陈代谢GM(1, 1)模型在建筑物沉降预测中的应用研究[J]. 城市勘测, 2008(3): 136-138. DOI:10.3969/j.issn.1672-8262.2008.03.043 |
| [3] |
郭江, 王全才, 程国平, 等. 灰色新陈代谢GM(1, 1)模型在高速公路滑坡中的变形预测研究[J]. 地质灾害与环境保护, 2016, 27(1): 86-90. DOI:10.3969/j.issn.1006-4362.2016.01.017 |
| [4] |
陈霞, 邱桃荣, 魏玲玲, 等. GM(1, 1)模型和新陈代谢模型的应用比较[J]. 微计算机信息, 2008(12): 157-159. DOI:10.3969/j.issn.1008-0570.2008.12.063 |
| [5] |
张锦秀, 徐丙振. GM(1, 1)灰色预测方法的改进[J]. 统计与决策, 2016(11): 16-18. |
| [6] |
张诚, 周湘峰. 基于灰色预测-马尔可夫链-定性分析的铁路货运量预测[J]. 铁道学报, 2007(5): 15-21. DOI:10.3321/j.issn:1001-8360.2007.05.003 |
| [7] |
曾贤敏, 黄腾, 李桂华, 等. 新陈代谢GM(1, 1)模型在大坝边坡沉降监测中的应用[J]. 测绘工程, 2015, 24(8): 53-56. DOI:10.3969/j.issn.1006-7949.2015.08.013 |
| [8] |
康超, 黄声享, 李洋洋. 小波去噪和新陈代谢GM(1, 1)相结合应用于变形预报[J]. 测绘地理信息, 2015, 40(6): 46-48. |
 2019, Vol. 44
2019, Vol. 44


