| 网络RTK参数全局化及其应用 |
2. 地球空间信息技术协同创新中心,湖北 武汉,430079;
3. 贵州省第一测绘院,贵州 贵阳,550025
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
3. The First Surveying and Mapping Institute of Guizhou Province, Guiyang 550025, China
在网络RTK中,基站数据处理通常采用单基线模式,求解基站间差分形式的相位模糊度、电离层延迟及对流层延迟等参数。服务中心为流动站提供的网络RTK数据,由流动站周围的3个基站(通常称为三角形小区)有关的观测数据和参数来生成[1-3]。在单基线模式下,各基线参数的基准并不统一,这是由于在进行基线数据处理时,参考站及参考星的选取可能不相同而引起的。在一个三角形小区中,各基线参数很容易利用基线间及卫星间的关系统一到一个共同的基准上(相对于共同参考站及参考星)。但不同小区间仍可能具有不同的基准。因此,当流动站仅在小区内运动时,网络RTK服务不会出现问题。但是当流动站在不同小区间漫游时,则可能会发生网络RTK数据基准的切换,这将引起流动站的重新初始化。为解决基准不一致的问题,瑞士徕卡(Leica)公司在研究主辅站技术时,提出了一种相位模糊度水平统一的方法[4, 5],该方法以参考星上的站间单差模糊度为基准,将基站间的站星双差模糊度归算到一个公共的水平。这种方法解决了相位模糊度参数的基准统一,但并未考虑其他参数的统一问题。
本文提出了参数全局化的概念,较为全面地解决了网络RTK中基线参数基准统一的问题。
1 参数全局化 1.1 参数全局化方法采用差分模型进行基线处理时,解求出参数的基准与处理时所选取的参考站和参考星有关。在分小区进行网络RTK基站数据处理时,若选取了不同的参考站或参考星,就会出现小区间基准不一致的情况。本文将上述各小区的参数称为局部参数。
为解决局部参数基准不一致的问题,本文提出了一种实现局部参数基准统一的方法。该方法将局部参数作为观测量,非差形式的参数(以下简称非差参数)作为待估参数,根据差分原理,建立全网局部参数与非差参数之间的关系,并采用最小二乘方法计算出非差参数,从而将所有的参数都统一到一个共同的基准上。本文将该过程称为参数全局化,并将由此过程所得出的非差参数称为全局参数。
根据非差、单差及双差之间的关系,全局参数S与采用双差模型所解求出的局部参数
| $ \nabla \Delta S_{m, n}^{{\rm{ref}}, j} = \left( {S_n^j - S_m^j} \right) - \left( {S_n^{{\rm{ref}}} - S_m^{{\rm{ref}}}} \right) $ | (1) |
式中,下标m、n为测站标识;上标ref、j为卫星标识,其中ref为参考星。参数全局化时,需要指定一个站作为参考站,指定一颗全网共视卫星作为参考星。与参考站及参考星有关的全局参数认为已知,作为参数全局化的基准。各相关值的确定可以采用如下方法:
1) 作为基准的相位模糊度参数通过伪距观测值来确定;
2) 作为基准的电离层延迟及对流层延迟参数通过经验模型获得(如电离层延迟可采用Klobuchar模型,对流层延迟可采用Saastamoinen模型等)。
对于每一局部参数,均可以按照式(1)列出观测方程。严格地说,全局参数的估计可分成相位模糊度参数及其他参数(电离层延迟及对流层延迟等)分别进行。在进行相位模糊度参数的全局化时,作为观测值的各相位模糊度局部参数可认为是等精度且不相关。在进行其他参数的全局化时,作为观测值的各相应局部参数的先验方差-协方差可采用单基线处理所得出的值。
实际应用中,为简化计算过程,全局参数的估计也可分成相位模糊度参数、电离层参数及对流层参数等3大部分,并且每一部分逐卫星单独进行。
1.2 网络RTK数据的生成模糊度固定后,提取出来的电离层延迟、对流层延迟等参数可用于生成网络RTK数据,本文主要研究的是虚拟参考站(vitual reference station,VRS)观测数据的生成。
1.2.1 利用局部参数生成VRS观测值利用局部参数生成的虚拟观测值可表示为:
| $ {O_{{\rm{VRS}}}} = {O_M} + \Delta {G_{M, V}} + \Delta {B_{M, V}} $ | (2) |
| $ \Delta {B_{M, V}} = \nabla \Delta {B_{M, V}} + \Delta {B_M} $ | (3) |
式中,Δ和
全局化后得到的全局参数为非差形式,利用全局参数生成VRS观测值的计算式为:
| $ \begin{array}{c} {O_{{\rm{VRS}}}} = {O_M} - {{B'}_M} + \Delta {G_{M, V}} + {{B'}_V}\\ = {O_M} + \Delta {G_{M, V}} + \left( {{{B'}_V} - {{B'}_M}} \right)\\ = {O_M} + \Delta {G_{M, V}} + \Delta {{B'}_{M, V}} \end{array} $ | (4) |
式中,B'为全局化后的电离层延迟、对流层延迟等全局参数。
综合式(2)和式(4)可知,采用局部参数或全局参数生成虚拟观测值时,两种方式的数学模型是等价的。
1.3 整体全局化与部分全局化由参数全局化的原理可知,当基站网是一个连通的整网时,所有基线参数都能参与全局化,本文将此种情况称为整体全局化。
然而,在网络RTK的基站数据处理过程中,由于网络传输滞后、观测数据不同步以及部分基线中相位模糊度难以固定等原因,会使部分基线解算滞后或无法得到固定解。为了保证解算效率及服务的可靠性,全局化过程不可能等到所有基线都解算完毕才开始进行,此时基站网可能是一个非完全连通的不完整网络,无法进行整体全局化,只能对各个已连通的子网单独进行参数全局化,本文称此种情况为部分全局化。
1.4 子网的划分图论中常将连通分量的个数作为图的连通性判断指标[6]。连通分量是一个图的极大连通子图。任何连通图的连通分量只有一个,即为其本身。图 1为一个连通的无向图G1,它仅有一个连通分量。对于图 2中的非连通无向图G2,它有两个连通分量。即若连通分量的个数为1,则该基站网是连通的整网;若连通分量个数大于1,那么基站网是非连通的。
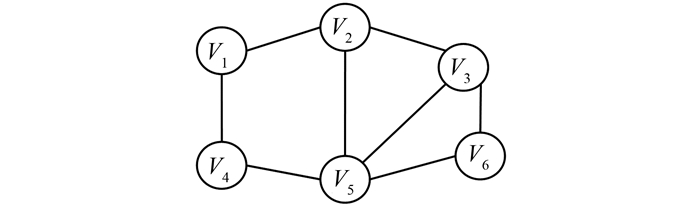 |
| 图 1 连通的无向图G1 Figure 1 Connected Undirected Graph G1 |
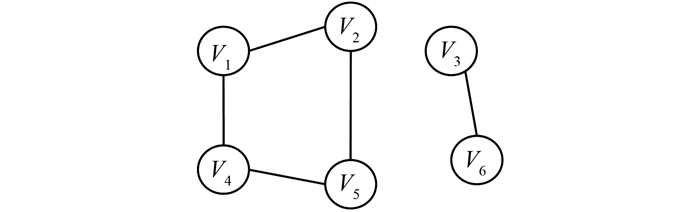 |
| 图 2 非连通图G2和它的两个连通分量 Figure 2 Unconnected Graph G2 and Its Two Connected Components |
当连通分量个数大于1时,基站网将会被划分为若干个子网,此时可通过提取无向图连通分量的方法来划分子网。
常用的连通分量提取方法主要有矩阵判别法[7]和遍历算法[8]。本文在提取无向图连通分量时采取深度优先搜索算法(depth-first search,DFS),图 3为深度优先遍历示意图,其中DFS遍历结果为:V0,V1,V2,V5,V4,V6,V3,V7。
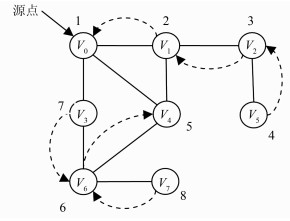 |
| 图 3 深度优先搜索示意图 Figure 3 Sketch Map of Depth-First Search |
每一次调用DFS后就得到了一个连通分量,调用DFS的次数就是图的连通分量的个数。每个连通分量中的顶点集和边集一起构成参与部分全局化的子网。
2 应用实例 2.1 相位模糊度确认参数全局化方法在获得全网统一的非差参数的同时,还能根据估计残差对参数进行检验。将该方法应用于相位模糊度参数,不仅可获得水平统一的相位模糊度,还能确认相位模糊度固定的正确性。
由于作为全局化过程中观测值的相位模糊度均为整数,在所有相位模糊度均正确固定的情况下,相位模糊度观测值的误差为0,因而全局化后其估计残差也均为0。若某个相位模糊度未能正确固定,则其误差不为0,且是一个整数,因而会使得全局化后估计残差中出现不为0的量。可以将相位模糊度参数全局化过程中的估计残差作为评判其固定是否正确的指标。
本文利用美国NGS CORS网2015年6月10日的观测数据所计算出的相位模糊度参数进行全局化,其基站网如图 4所示。
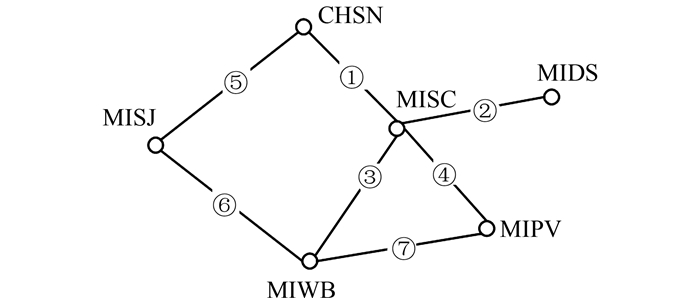 |
| 图 4 基站网构成图 1 Figure 4 Reference Stations Network One |
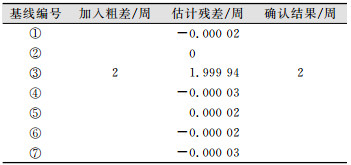
在对G02卫星上的相位模糊度参数进行全局化时,本文在基线③(MIWB-MISC)相应的相位模糊度上加入了两周的粗差。进行参数全局化时,采用IGG方案进行抗差估计[9],最后将残差取整,即得到相位模糊度的错误值,其结果如表 1所示。
| 表 1 模糊度确认结果 Table 1 Results of the Ambiguity |
 |
必须指出的是,确认相位模糊度参数的正确性及错误相位模糊度所含偏差的能力与网络结构具有密切的关系[10, 11]。
2.2 电离层、对流层延迟质量改善参数全局化中的观测量为局部参数,记为L,而全局化后得到的差分形式的全局参数
| $ \mathit{\boldsymbol{\hat L}} = \mathit{\boldsymbol{L}} + \mathit{\boldsymbol{V}} $ | (5) |
由参数估计方法可知[12]:
| $ {\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{\hat L\hat L}}}} = {\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{LL}}}} - {\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{VV}}}} $ | (6) |
可见,相比未全局化的局部参数L,差分形式的全局参数
为验证全局化方法对电离层延迟和对流层延迟参数质量的改善作用,本文采用了两种方法:①方法一:将全局化后的电离层延迟、对流层延迟进行内插,生成虚拟观测值用于流动站进行定位解算,然后与流动站的已知精确坐标进行对比,计算得到定位误差;②方法二:略去电离层延迟、对流层延迟的全局化过程,计算其定位误差。
同样选取美国NGS CORS网2015年6月10日的观测数据所计算出的电离层、对流层延迟参数进行全局化,其基站网如图 5所示。该基站网中,平均基线长度约为90 km。图 6为定位误差对比图。表 2为定位误差的均方根值。
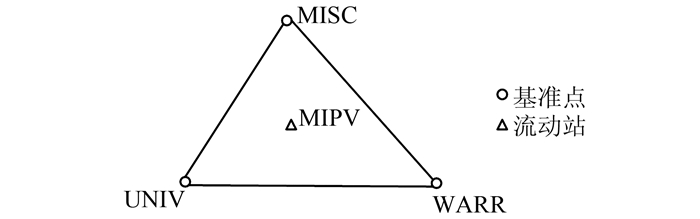 |
| 图 5 基站网构成图 2 Figure 5 Reference Stations Network Two |
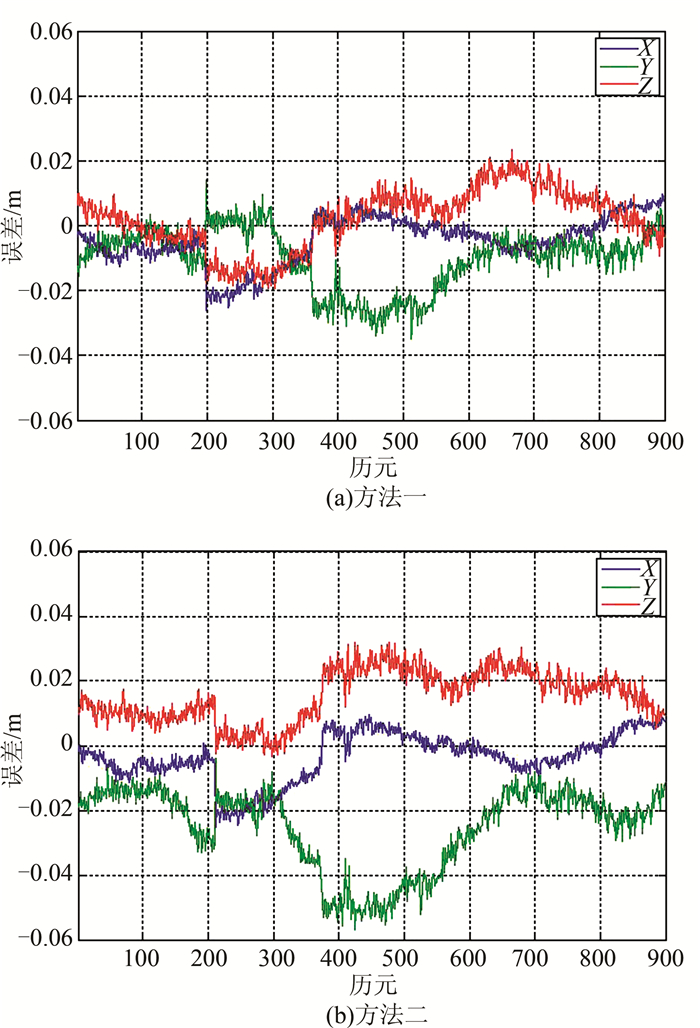 |
| 图 6 定位误差 Figure 6 Positioning Error |
| 表 2 定位误差的均方根误差/cm Table 2 Root Mean Square of Positioning Error/cm |
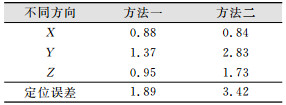 |
由表 2可知,方法一中的定位误差为1.89 cm,小于方法二中的定位误差。可见,全局化方法能够明显改善电离层延迟和对流层延迟的精度,提高定位精度。
3 结束语针对基准站网中各小区中相位模糊度、电离层延迟、对流层延迟等局部参数基准不统一的问题,本文提出了参数全局化方法及其处理策略,并进一步给出了确定部分全局化子网的算法。实验表明,参数全局化方法不仅可以进行模糊度确认,还能改善电离层延迟、对流层延迟等参数的质量。
| [1] | 李征航, 何良华, 吴北平. 全球定位系统(GPS)技术的最新进展第二讲网络RTK[J]. 测绘信息与工程, 2002, 27(2): 22–25 |
| [2] | 柯福阳, 王庆, 潘树国, 等. VRS网络RTK关键算法与技术及精度分析[J]. 宇航学报, 2009, 30(3): 1 287–1 292 |
| [3] | 高星伟, 陈锐志, 赵春梅. 网络RTK算法研究与实验[J]. 武汉大学学报·信息科学版, 2009, 34(11): 1 350–1 353 |
| [4] | Euler H J, Keenan C R, Zebhauser B E, et al. Study of a Simplified Approach in Utilizing Information from Permanent Reference Station Arrays[C]. Proceedings of the Institute of Navigation, ION GPS 2001, Salt Lake City, UT, USA, 2001 |
| [5] | Euler H J, Seeger S, Zelzer O, et al. Improvement of Positioning Performance Using Standardized Network RTK Messages[C]. Proceedings of the Institute of Navigation National Technical Meeting, ION NTM 2004, San Diego, CA, USA, 2004 |
| [6] | 卢开澄, 卢华明. 图论及其应用[M]. 北京: 清华大学出版社, 1998 |
| [7] | 耿素云, 屈婉玲, 张立昂. 离散数学[M]. 北京: 清华大学出版社, 2005 |
| [8] | 严蔚敏, 吴伟民. 数据结构及应用算法教程[M]. 北京: 清华大学出版社, 2002 |
| [9] | 周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115–120 |
| [10] | 黄声享, 王金岭. 多余观测分量与可靠性度量指标研究[J]. 武汉测绘科技大学学报, 1997, 22(2): 114–118 |
| [11] | 闫志跃, 喻国荣, 杨徉. 基于多余观测分量的整周模糊度可靠性检验方法[J]. 航天控制, 2015, 33(3): 88–93 |
| [12] | Koch K R. Least Squares Adjustment and Collocation[J]. Bulletin Geodesique, 1997, 51(2): 127–135 |
 2018, Vol. 43
2018, Vol. 43

