| 基于VC++6.0的附有参数的条件平差的设计与实现 |
最常见的测量工作是确定某些几何量的大小,如为了确定点的高程建立水准网,确定点的坐标而建立平面控制网或三维网[1, 2]。但实际的平差问题需要选择建立函数模型,形象描述观测量与未知量之间的数学函数关系的模型。测量平差的目的是为了最佳估计观测值函数的未知量,而不同函数的未知量可视实际平差问题进行选择。未知量为待测观测量的平差值,建立的关系几何模型中t个独立参数为未知量,函数模型的形式与条件方程有差异,所建立的函数模型是将观测量表达为t个独立参数的函数,这些不同未知量的估计有相应的平差方法。
本文以VC++6.0为基本编程工具,运用附有参数的条件平差方法,利用VC++6.0软件,根据误差理论与测量平差课程设计指导书中给出的筠州大桥的平面控制网系列数据,得到了筠州大桥平面控制网观测数据的参数和未知点的改正数。结果表明,附有参数的条件平差利用软件实现是可行的。
1 平差模型假设测量平差中的观测值个数为n,已知的必要观测数为t,那么多余观测数r=n-t,若不增选参数,只需列出r个条件方程,称为条件平差法。如果选u个独立量为参数进行平差计算,其中0<u<t,在满足这个条件的情况下,可以建立符合要求含有参数的条件方程作为测量平差的函数模型,称为附有参数的条件平差法[3, 4]。
| $ \underset{c\times n}{\mathop{\mathit{\boldsymbol{A}}}}\,\underset{n\times 1}{\mathop{\mathit{\boldsymbol{V}}}}\,\text{+}\underset{c\times u}{\mathop{\mathit{\boldsymbol{B}}}}\,\underset{u\times 1}{\mathop{{\mathit{\boldsymbol{\hat{x}}}}}}\,\text{+}\underset{c\times 1}{\mathop{\mathit{\boldsymbol{W}}}}\,\text{=}\underset{c\times 1}{\mathop{\bf{0}}}\, $ | (1) |
式中,V为观测值L的改正数;
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{P}}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{K}}\\ {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{K}} = 0 \end{array} \right. $ | (2) |
将得到的基础方程通过转换可以得到其对应的法方程为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{N}}_{aa}}\mathit{\boldsymbol{K}} + \mathit{\boldsymbol{B\hat x}} + \mathit{\boldsymbol{W}} = 0\\ {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{K}} = 0 \end{array} \right. $ | (3) |
由此推算得出参数改正数和观测值改正数为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat x}} = - \mathit{\boldsymbol{N}}_{bb}^{ - 1}{\mathit{\boldsymbol{B}}^T}\mathit{\boldsymbol{N}}_{aa}^{ - 1}\mathit{\boldsymbol{W}}\\ \mathit{\boldsymbol{V}} = - {\mathit{\boldsymbol{P}}^{ - 1}}{\mathit{\boldsymbol{A}}^T}\mathit{\boldsymbol{N}}_{aa}^{ - 1}(\mathit{\boldsymbol{B\hat x}} + \mathit{\boldsymbol{W}}) \end{array} \right. $ | (4) |
计算观测值平差值为:
| $ \mathit{\boldsymbol{\hat L}} = \mathit{\boldsymbol{L}} + \mathit{\boldsymbol{V}} $ | (5) |
精度评定为:
| $ \hat \sigma _0^2 = \frac{{{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}}}}{r} $ | (6) |
1) VC++6.0的开发环境。VC++6.0是基于Windows平台的可视化集成开发环境,集源程序的编写、编译、连接、调试、运行以及应运程序的文件管理于一体,因为其强大的功能全完可以获得Internet的网络支撑,在各类计算机语言开发对象中显示出独特方便的特点,成为目前最为流行的C++程序开发环境之一[7]。
2) VC++6.0附有参数的条件平差的设计。在学习了条件平差之后,对于含有n个观测值和t个必要观测且n>t的条件平差问题,列出r个独立的条件方程便可以进行后面一系列数值的条件平差计算。但是,在给出不同要求的实际条件下,难免会有r个或者少于r个完全独立的符合要求的条件方程没有办法列出[8-11]。在本次附有参数的条件平差中,利用附有参数的条件的函数模型[11]根据式(1)~式(4)依次编程,得到参数和观测值的改正数。在运行时,打开建立的B.TXT、P.TXT和L.TXT文件,编译运行得到最终结果。
3) 附有参数条件平差的VC++6.0编程及实现。在符合实际项目要求的前提下,建立附有参数的条件平差的平差函数模型,用VC++6.0进行编译设计时,首先输入观测值总数、已设置好的权阵的维数和方程系数矩阵B的列数;然后,编译运行界面显示出观测值的改正数和参数改正数;最后,编译运行后可得到符合要求的观测值和参数的改正数。
3 实例分析1) 控制网基线观测数据。本次的实验数据是误差理论与测量平差课程设计指导书中提供的筠州大桥的平面控制网系列数据(以D1~D6分别表示DQ1~DQ6),设计院提供了两个导线点D4和D5,用索佳SET2110全站仪用前方交会法与原D2坐标(x=146 096.554, y=502 089.709)比较,X坐标差值为-2 mm, Y坐标的差值为1 mm,精度高即作为筠州大桥平面控制网的基准点,以D2-D1的方向为起算方向[12]。
2) 平面控制网的布设与外业观测。筠州大桥根据所处的地形,将平面控制网点布置在锦江河上游。根据布设好的平面控制网点位,采用经鉴定加常数为2.35 mm的全站仪进行观测[13]。按照四等精度要求,角度观测6个测回,距离观测2个测回。观测过程中,一测回内2C值(两倍照准差值)不符合规范的限制度数时,必须重新观测[14];筠州大桥控制网平面布置图如图 1所示,筠州大桥平面控制网方向观测值如表 1所示。
 |
| 图 1 控制网平面布置图 Fig.1 Plane Control Network Layout |
| 表 1 筠州大桥控制点D1方向观测值 Tab.1 Bridge of Junzhou Control Points D1 Direction Observation |
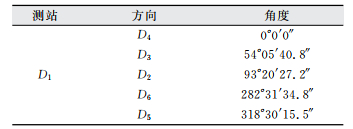 |
根据要求在进行边长观测时,一测回边长观测值互差不超过2 mm,往返测边长值互差不超过5 mm,否则重测,筠州大桥平面控制网边长观测值如表 2所示。
| 表 2 平面控制网部分边长观测值 Tab.2 Control Network Section Observation Length |
 |
所有经过全站仪观测的外业观测成果中边长经加常数、乘常数改正后,进行严密检核,最后完成点D1~D6的坐标平差值计算。
3) VC++6.0运行实现。运用上述观测数据和附有参数的条件平差模型列出附有参数的条件方程式,由已知的条件方程式得出:n=33,t=10,r=23。
在运行时,打开已经统计好的B.TXT、P.TXT、L.TXT文件进行软件操作。通过运算出的改正数计算观测值平差值,根据点位精度的运算方程式得出观测值平差值、坐标估计值和点位误差如表 3所示,精度在1~2 mm,符合要求。
| 表 3 控制点坐标平差值、坐标估值和点位精度 Tab.3 Control Point Coordinate Adjustment Value, Coordinate Estimated Value and Point Precision |
 |
4 结束语
通过本文的分析可知,VC++6.0运行实现附有参数的条件平差模型是可靠的,而且点位精度较高,符合实际要求。利用VC++6.0编译出间接平差,分析间接平差与条件平差之间的关系,计算出的改正数精度较高,符合要求。在求解个别非直接观测量的平差值与精度和当条件方程式通过直接观测量难以列立时,附有参数的条件平差方法是最适合可行的,解决了列立条件式存在的问题。
基于平差理论、大地测量学以及工程测量学等[15],利用VS2010软件开发平台对控制网进行平差和优化设计等编程的实现,说明测量数据用软件实现快速准确的平差计算是可行的。
| [1] |
Vosselman G, Maas H G. Airborne and Terrestrial Laser Scanning[M]. Dunbeath: Whittles Publishing, 2010.
|
| [2] |
李沛鸿, 江红兵, 王劲松. 基于MatrixVB的测量平差程序设计与实现[J]. 北京测绘, 2012(4): 14-18. DOI:10.3969/j.issn.1007-3000.2012.04.005 |
| [3] |
隋立芬, 宋力杰, 柴洪洲. 误差理论与测量平差基础[M]. 北京: 测绘出版社, 2010.
|
| [4] |
武汉大学测绘学院测量学科组. 误差理论与测量平差基础[M]. 3版. 武汉: 武汉大学出版社, 2014.
|
| [5] |
胡圣武, 肖本林. 误差理论与测量平差基础[M]. 北京: 北京大学出版社, 2012.
|
| [6] |
王穗辉. 误差理论与测量平差基础[M]. 2版. 上海: 同济大学出版社, 2015.
|
| [7] |
曾辉, 王更生, 李广丽. C++程序设计实训教程[M]. 北京: 北京邮电大学出版社, 2009.
|
| [8] |
金日守, 戴华阳. 误差理论与测量平差基础[M]. 北京: 测绘出版社, 2011.
|
| [9] |
张俊, 袁亮, 张鹏飞. 条件平差和间接平差模型应满足的两个等式关系[J]. 测绘与空间地理信息, 2014, 37(12): 86-87. DOI:10.3969/j.issn.1672-5867.2014.12.026 |
| [10] |
胡圣武, 王育红. 教学中消除限制条件的条件平差求解方法探讨[J]. 测绘科学, 2014, 39(12): 151-154. |
| [11] |
李飞, 纪淑鸳. Excel在测量平差中的应用——以条件平差为例[J]. 水利与建筑工程学报, 2014, 12(1): 197-200. |
| [12] |
武汉大学测绘学院测量学科组. 误差理论与测量平差课程设计指导书[M]. 武汉: 武汉大学出版社, 2014.
|
| [13] |
马飞虎. 土木工程测量[M]. 长沙: 中南大学出版社, 2016.
|
| [14] |
韦宏鹄. 土木工程测量[M]. 西安: 西安交通大学出版社, 2015.
|
| [15] |
连达军, 严勇, 郑留蒋, 等. 《工程测量学》课程设计系统设计与开发[J]. 测绘地理信息, 2016, 41(6): 95-99. |
 2018, Vol. 43
2018, Vol. 43

