| 多波束水深数据质量评定方法研究 | [PDF全文] |
2. 海军出版社,天津, 300450
2. Navy Publishing Company, Tianjin 300450, China
随着多波束测深技术在海底地形测量中广泛应用,多波束数据质量评定一直是国内外学者研究的重点问题[1, 2]。由于海水的动态特性及多波束系统的复杂性,水深测量误差具有多源性、无重复观测等特点。对多波束数据误差来源,国内外学者做了大量工作,取得了一致成果[3, 4]。在测量数据的后处理中,需对其进行声速改正、涌浪改正、潮位改正及粗差剔除,利用改正后的水深数据形成成果图。
目前,国内尚没有一个统一的多波束数据处理技术标准,缺乏完善的多波束质量评价体系,中国海道测量规范规定了主测线和检查线重合点水深差值范围,国际海道测量规范规定了多波束水深测量要用多余观测来检查测深质量[5, 6]。多波束数据质量统计方法[7, 8]分析了多波束不确定度模型的计算方法。国际水文组织(International Hydrographic Organisation,IHO)规定了水深点测量垂直不确定度最大值。本文利用软件处理多波束测量数据,计算各水深点对应的水深不确定度,通过本文方法检验主检线水深不确定度的符合情况,通过实例验证,Caris与Perspective软件中计算的不确定度合理,为多波束数据质量评定和多波束处理软件的选择提供了理论支持。
1 多波束数据不确定度测量不确定度是目前对于多波束测量数据质量的最新理解和阐述,以前用测量误差来表述,但两者具有完全不同的含义。测量不确定度的含义是指由于测量误差的存在,对测量值不能肯定的程度,反过来也表明该结果的可信赖程度。测量不确定度是测量结果质量的指标,既便于评定其可靠性,又增强了结果之间的可比性。一方面可通过对观测序列进行统计分析的方法来评定测量垂直不确定度,如实验室静态重复测量法,即在同一测量条件下,对同一对象多次重复测量,统计其误差,给出某置信区间对应的不确定度;另一方面测量垂直不确定度由若干分量组成,可按各组成分量的方差和协方差计算测量垂直不确定度。不确定度对应的海底置信区域示意如图 1所示。
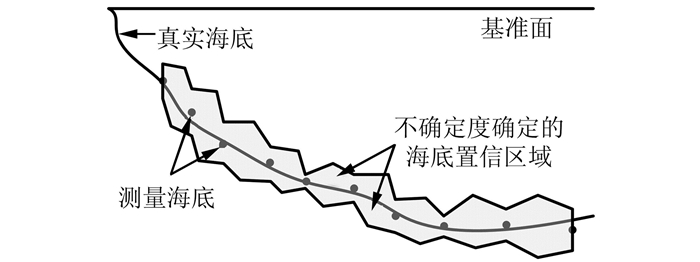 |
| 图 1 顾及不确定度的海底示意图 Fig.1 Seafloor Schematic with Uncertainty |
多波束测深系统在垂直方向上的不确定度uv(对应95%的置信区间)计算模型参见文献[7]。而IHO中规定了不同水深对应的水深垂直不确定度为:式中,不同水深对应的水深不确定度最大值的参数值如表 1所示。
| $ {u_v} = \sqrt {{a^2} + {b^2}{h^2}} $ | (1) |
| 表 1 不同水深对应的水深不确定度最大值 Tab.1 Maximum Uncertainty of Water Depth Corresponding to Different Water Depths |
 |
2 交叉区域水深不确定度计算方法
国际标准化组织(International Organization for Standardization, ISO)推荐不确定度的合成方法为:当观测结果y与多个观测量(x1, x2, …, xN)组成函数y=f(x1, x2, …, xN)时,则观测结果y的不确定度uc(y)由这N个观测量的不确定度u(xi),i=1, 2, …, N以一定的传播规律联合构成,即
| $ {u_c}(y) = \sqrt {\sum\limits_{i = 1}^N {{{\left( {\frac{{\partial f}}{{\partial {x_i}}}} \right)}^2}} {u^2}\left( {{x_i}} \right) + 2\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^N {\left( {\frac{{\partial f}}{{\partial {x_i}}}} \right)} } \left( {\frac{{\partial f}}{{\partial {x_j}}}} \right)u\left( {{x_i}} \right)u\left( {{x_j}} \right){r_{{x_i}{x_j}}}} $ | (2) |
式中,rxixj为xi与xj的相关系数。
交叉区域重合点的水深值分别为d1, i与d2, i,对应的垂直不确定度分别为u1, i与u2, i,i=1, 2, …, N,其中d1, i、u1, i为主测线水深值与垂直不确定度,d2, i与u2, i为检查线水深值与垂直不确定度,根据式(2)重合点水深差值Δdi对应的合成垂直不确定度可由u1, i与u2, i联合确定,即
| $ \begin{array}{l} {u_v}\left( {\Delta {d_i}} \right) = \\ \sqrt {{u^2}\left( {{d_{1,i}}} \right) + {u^2}\left( {{d_{2,i}}} \right) - 2u\left( {{d_{1,i}}} \right)u\left( {{d_{2,i}}} \right){r_{{d_{1,i}}{d_{2,i}}}}} \end{array} $ | (3) |
为便于讨论,假设重合点水深相互独立,即rd1, id2, i=0,则式(3)可化为:
| $ {u_v}\left( {\Delta {d_i}} \right) = \sqrt {{u^2}\left( {{d_{1,i}}} \right) + {u^2}\left( {{d_{2,i}}} \right)} $ | (4) |
事件Δdi<uv(Δdi)发生的概率P(Δdi<uv(Δdi))<95%。事实上,并不是所有点水深差值均落在95%的置信区间内。因此,设交叉区重合水深点水深差值Δdi落在区间[0, uv(Δdi)]的个数为n,该组水深数据质量的保证率为η,则
| $ \eta ={n}/{N}\; $ | (5) |
1) 试验区域。选取某海区SeaBat8125型多波束主测线与检查线实测数据,其水深变化范围为21.14~26.88 m。本文分别使用软件Caris 6.1和Triton公司Perspective 7.6处理多波束数据,处理过程包括定位延时改正、升沉改正、潮位改正、声速改正和粗差剔除,计算各水深点对应的垂直不确定度,并生成海底立体空间曲面,并按0.8 m的格网大小输出水深数据及其垂直不确定度。
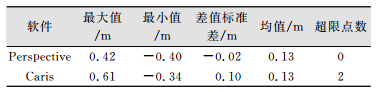
2) 多波束数据质量分析。对交叉区域重合点水深差值按交叉检查法进行统计,结果如表 2所示。从表 2中可以看出,Perspective软件处理后的多波束水深差值的均值、极值和超限点数均小于Caris软件的处理结果。
| 表 2 传统交叉区域重合点水深对比 Tab.2 Water Depth Contrast of Traditional Cross Regional Overlap Points |
 |
事实上,对于多波束测深数据,某ping各接收方向上的水深垂直不确定度并不是相同的,图 2给出了主测线某ping各水深垂直不确定度与接收方向的关系,其中,虚线自下而上依次为该ping各水深对应的特等、1等和2等测量不确定度。从图 2中可以看出,中央波束对应的水深不确定度明显小于边缘波束对应的水深不确定度,且边缘波束不确定度容易超限。
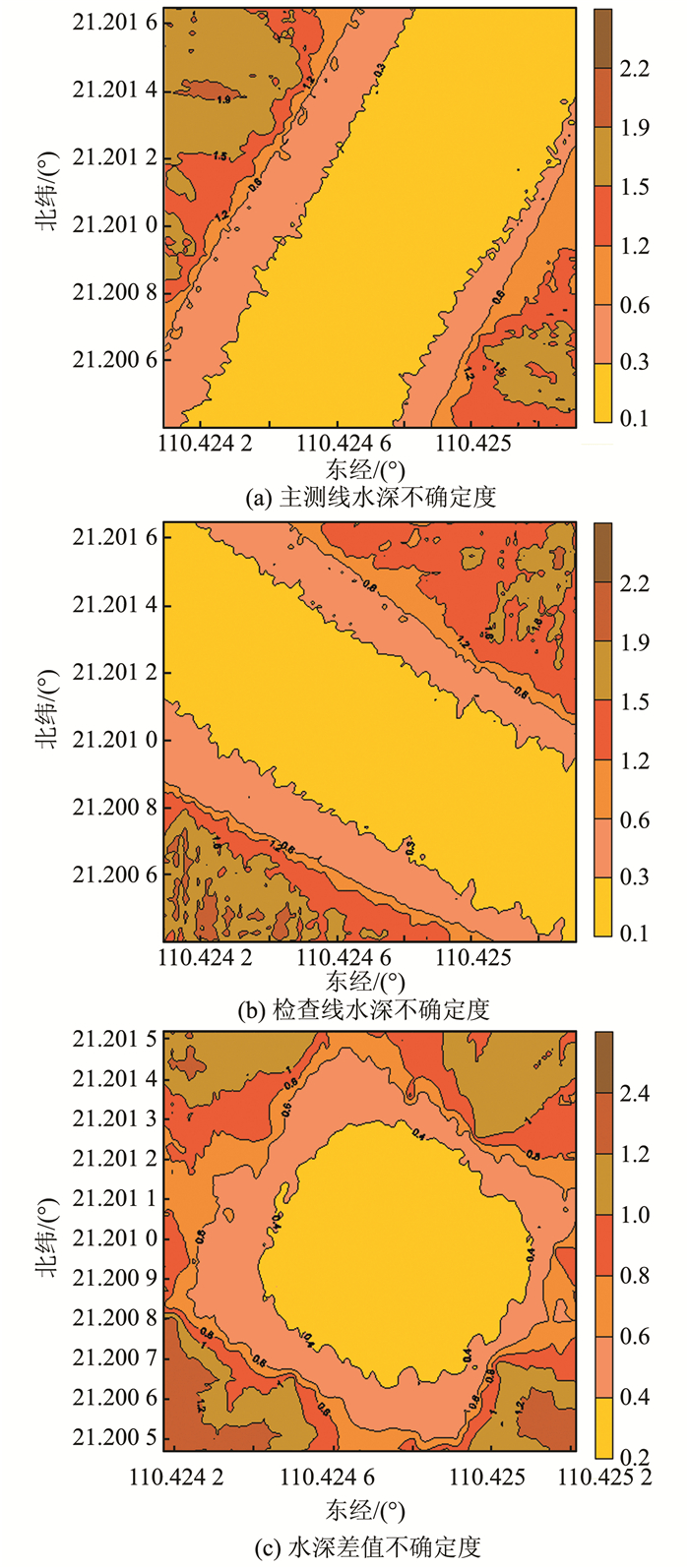 |
| 图 2 交叉区域不确定度等值线图 Fig.2 Cross Region Uncertainty Isoline Map |
为了更全面地反映交叉区域水深及水深差值的不确定度,分别构建交叉区域主测线水深(图 2(a))、检查线水深(图 2(b))及水深差值不确定度等值线图(图 2(c))。无论是主测线、检查线水深不确定度还是水深差值不确定度,在不同区域的不确定度均变化较大,证实了独立等精度质量检核方法的缺点。
根据式(4)和式(5),本文对试验区域19 214个点水深进行质量检核,结果如表 3所示。可以看出,Caris与Perspective软件处理的水深数据,在交叉区域均有少量点的水深差值与所计算的不确定度不符,且Caris软件中处理的不符点数大于Perspective软件中的不符点数。
| 表 3 交叉区域重合点水深质量检核结果 Tab.3 Checking Results of Water Quality in Coincidence Area of Cross Area |
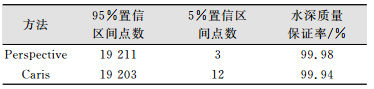 |
传统交叉检查法检查的水深不符值主要存在于主检线水深差值大的水深点处,而本文的检核方法本质是主检线水深差值与不确定度是否相符,对于水深差值大的水深点处,若计算的水深质量保证率较大,则认为该水深差值可信。由表 3可以看出,不同的多波束处理软件得到成果数据并不一致,同时,在不确定度较小的区域更容易出现水深差值与不确定度不符的现象。本文试验中,Perspective软件得到的成果水深与其不确定度比Caris软件符合得更好。
4 结束语各水深点无重复观测,无法从统计意义上给出各水深点不确定度。由于当前各多波束处理软件采用相关模型估计水深点的不确定度,存在一定的误差,本文所提方法可有效检查出不确定度不符的水深点。
本文仅选取一个试验海区的多波束水深进行试验,如何用更多的数据源验证多波束水深数据质量,有待以后进一步研究。
| [1] |
刘雁春, 肖付民, 暴景阳, 等. 海道测量概论[M]. 北京: 测绘出版, 2006.
|
| [2] |
王中宇, 刘智敏, 夏新涛, 等. 测量误差与不确定度评定[M]. 北京: 科学出版社, 2008.
|
| [3] |
李家彪, 郑玉龙, 王小波, 等. 多波束测深及影响精度的主要因素[J]. 海洋测绘, 2001(1): 26-32. DOI:10.3969/j.issn.1671-3044.2001.01.003 |
| [4] |
朱庆, 李德仁. 多波束测深数据的误差分析与处理[J]. 武汉测绘科技大学学报, 1998, 23(1): 1-4. DOI:10.3321/j.issn:1671-8860.1998.01.001 |
| [5] |
IHO. IHO Standards for Hydrographic Surveys: S-44[S]. Monaco: International Hydrographic Bureau, 2008
|
| [6] |
吴英姿, 徐新盛, 乔力争. 多波束测深系统的精度评估方法研究[J]. 海洋技术, 2003, 22(3): 65-69. DOI:10.3969/j.issn.1003-2029.2003.03.014 |
| [7] |
吴超, 殷晓冬, 张立华, 等. 基于不确定度的多波束测深数据质量评估方法[J]. 海洋测绘, 2009, 29(5): 11-14. DOI:10.3969/j.issn.1671-3044.2009.05.004 |
| [8] |
殷晓冬, 李宜龙, 周君华, 等. 基于Ping的多波束测深精度评估方法研究[J]. 测绘通报, 2007(3): 8-11. DOI:10.3969/j.issn.0494-0911.2007.03.002 |
 2019, Vol. 44
2019, Vol. 44

