| 基于非组合精密单点定位的区域电离层建模 |
2. 武汉大学测绘学院, 湖北 武汉, 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
随着全球导航卫星系统(global navigation satellite system,GNSS)技术的发展,利用GNSS观测值进行电离层建模是当前电离层研究领域的热点和难点,若干国际组织利用分布在全球测站的观测数据定期发布三维全球电离层云图产品,此产品为和电离层相关的空间研究提供了参考。此外,部分GNSS地基增强系统提供区域电离层产品以辅助GNSS定位,实现快速、可靠的定位应用。对于单频实时导航定位用户而言,采用有效的电离层改正模型可以很好地削弱该误差影响。如GPS导航电文中的电离层模型可以消除60%左右的延迟误差,广域增强系统(wide area augmentation system,WAAS)差分改正中格网电离层模型可以消除80%以上的误差[1]。常用的电离层改正模型有Klobuchar模型和GIM模型等,相关实验表明,对于高、中、低纬度地区,标准单点定位(standard point positioning,SPP)解算选择GIM模型明显优于采用Klobuchar模型[2]。联合双频GPS数据,利用相位平滑伪距算法,可得到包含斜向电离层总电子含量、测站和卫星差分码偏差的电离层观测值,常应用于与电离层有关的研究。然而,平滑伪距电离层观测值易受平滑弧段长度和与测站有关的误差影响。利用非组合精密单点定位(precise point positioning,PPP)技术计算PPP电离层观测值,进而估计斜路径电子含量(slant total electron content,STEC)和站星码间偏差(differential code bias,DCB)。
利用GNSS对电离层进行研究的前提条件是在GNSS观测值中提取出有效的电离层信息。当前,利用GNSS双频(多频)观测数据计算电离层主要的方法如下:①利用无几何距离(geometry free,GF)组合的码观测值计算电离层,易受与测站相关的影响(如观测噪声和多路径效应)[2];②利用GF组合的相位观测值计算电离层,此方法模糊度参数多[3];③联合GF组合的码观测值和相位观测值,通过相位平滑伪距的方法计算电离层观测值,易受到平滑弧段长度及与测站相关的误差影响[4-7];④利用双差模糊度固定的相位观测值计算电离层观测值。
本文基于非组合PPP的方式估计电离层延迟量,利用某省连续运行参考站系统(continuously operating reference stations,CORS)站一天的观测数据,固定站坐标、利用国际GNSS服务(international GNSS service,IGS)产品改正相关误差,对求解出的天顶方向总电子含量(vertical total electron content,VTEC)利用纬度差和太阳时角差的多项式拟合进行区域电离层建模,建立该省在单天内的电离层模型。将多项式拟合建模的结果与PPP计算值作比较,分析模型的可行性。
1 PPP电离层观测值计算1) 电离层观测值。标准PPP的算法是采用消电离层组合观测值作为观测量,消除了观测值中电离层的影响,该方法不便于进行电离层研究。本文采用的非组合PPP算法,将电离层作为待估参数与对流层延迟、接收机钟差、整周模糊度一并估计。基于原始观测值的非组合PPP模型参考文献[1]。
IGS发布的精密卫星钟差及电离层参数的表达方式推导过程参考文献[8],电离层观测值I1, c为:
| $ {I_{1, c}} = {I_1} + \frac{{f_2^2}}{{f_1^2 - f_2^2}} \times {\rm{DCB}} $ | (1) |
式中,f1和f2为频率;I1为L1上的电离层延迟。
利用GAMIT解算软件解得的坐标作为已知坐标,利用IGS发布的轨道和钟差产品作为已知值代入方程,则基于原始观测值的观测方程改为:
| $ \left\{ \begin{array}{l} {L_1} = T_r^s + c\;{\rm{d}}{{\rm{t}}_r} + {I_{1, c}} + {\lambda _1}{N_1} + {\varepsilon _{{L_1}}}\\ {L_2} = T_r^s + \mathit{c}\;{\rm{d}}{{\rm{t}}_r} + \mu {I_{1, c}} + {\lambda _2}{N_2} + {\varepsilon _{{L_2}}} \end{array} \right. $ | (2) |
式中,L1、L2分别为频率f1、f2的载波相位观测值;Trs为对流层延迟;cdtr为接收机钟差;μ为电离层系数;λ为波长;εL1、εL2分别为两个频率的观测噪声;N为整周模糊度。
2) 待估参数解算策略。由于固定站坐标和采用IGS产品,本文中的待估参数仅为对流层延迟Trs,接收机钟差cdtr,f1频率上的电离层延迟I1, c,整周模糊度N,减少了待估参数个数,有效提高了参数估计效率。本文采用了正反双向卡尔曼滤波,以反向滤波的结果作为最终结果用于电离层建模。
2 区域电离层建模目前,解决电离层延迟误差的方法一般有双频改正法、差分GPS定位法、半和改正法和电离层模型法。现有的电离层模型基本上可以分为两类:①依据建立模型以前很长时期内的观测资料建立起来的反映电离层变化规律的经验公式,如Bent模型、Klobuchar模型、IRI模型等,由于影响电离层因素很多而且随意性较强,研究者对各个因素相互关系和作用机制及变化规律未完全清楚,所以这些模型的精度一般不太高;②依据某时段在某区域的实测的电离层延迟采用数学方法拟合出一个模型,这种方法不需要对电离层变化规律有透彻的了解,一些不规则的变化也可以在模型中得到反映。
常用的电离层延迟改正模型包括Geogiadiou三角级数展开模型、低阶球谐函数展开模型和多项式函数模型[9, 10]。其中,多项式函数模型是一种结构简单,能顾及电离层随纬度、太阳时角变化特征的一种模型,在小区域范围内取得较好的拟合结果,但是多项式函数模型的局限性是需要利用数个小时的数据才能达到一个理想的精度水平。
为了简化计算,本文采用单层电离层模型,即假定电离层中所有自由电子集中在一个薄层上,用这个薄层代替整个电离层,用H表示该薄层高度,本文取H=350 000.0 m。
本文利用纬度差和太阳时角差的多项式进行区域电离层建模,有关实验表明,在小范围区域内,该方法可以取得较好的拟合效果[11]。
选择电离层单层模型的投影函数为:
| $ \left\{ \begin{array}{l} z' = {\rm{arcsin}}\left[ {\frac{R}{{R + H}}{\rm{cos}}z} \right]\\ F\left( {z'} \right) = \frac{1}{{{\rm{cos}}z'}} \end{array} \right. $ | (3) |
式中,z′为穿刺点处天顶距;z为卫星天顶距;R为地球平均半径;F(z′)为投影函数。
多项式函数模型结构简单,顾及到电离层随纬度和太阳时角的变化特征,模型公式为:
| $ {\rm{VTEC}} = \mathop \sum \limits_{i = 0}^n \mathop \sum \limits_{j = 0}^m {E_{ij}}{\left( {\varphi - {\varphi _0}} \right)^i}{\left( {S - {S_0}} \right)^j} $ | (4) |
式中,Eij为模型拟合系数;φ、φ0分别为穿刺点、拟合区域中心的地理纬度;S、S0分别为穿刺点、拟合区域中心的太阳时角;m、n为多项式拟合阶数,本文取m=3,n=4,在小范围区域即可满足要求[12]。电离层延迟量I与总电子含量(TEC)的关系为:
| $ I = \pm {\rm{ }}\frac{{40.3}}{{{f^2}}}{\rm{TEC}} $ | (5) |
顾及式(4)和式(5),将式(1)改写为[13]:
| $ \begin{array}{l} \frac{{{I_{1, c}}}}{Q} = F\left( {z'} \right) \times \mathop \sum \limits_{i = 0}^n \mathop \sum \limits_{j = 0}^m {E_{ij}}{\left( {\varphi - {\varphi _0}} \right)^i}\left( {S - } \right.\\ \;\;\;\;\;\;\;\;\;{\left. {{S_0}} \right)^j} + {\rm{ }}\frac{{f_2^2}}{{f_1^2 - f_2^2}} \times \frac{{{\rm{DCB}}}}{Q} \end{array} $ | (6) |
式中,
实验选取了XZCH、BTDH、BTSA、BBSN、XZXD和JSXY6个测站,其中,JSXY作为检验建模效果的测站,不参与建模。相邻测站距离最大为77.9 km,最小27.4 km,平均距离为48.4 km。实验数据采用2015年年积日004的全天数据,采样间隔为15 s,截止高度角为15°。
实验采用PPP方式解算电离层延迟量(转换为TECU, 1 TECU=1016个电子),并逐历元计算穿刺点坐标、太阳时角和电离层投影函数值。使用5个站的解算结果,选取2 h为一个时段,将求得的电离层延迟量代入式(5),每个时段求解一组多项式系数。根据穿刺点坐标、太阳时角和电离层投影函数,计算出对应历元、对应卫星的电离层的TECU,与PPP解得的TECU相比较。
图 1仅选取BTSA站与XZCH站逐历元的模型值与解算值的差值绝对值。测站XZCH、BTDH、BTSA、BBSN和XZXD所接收到的测站所有历元的卫星TECU值均方差依次为:8.618、6.579、4.599、7.358和9.018,平均值为7.704。
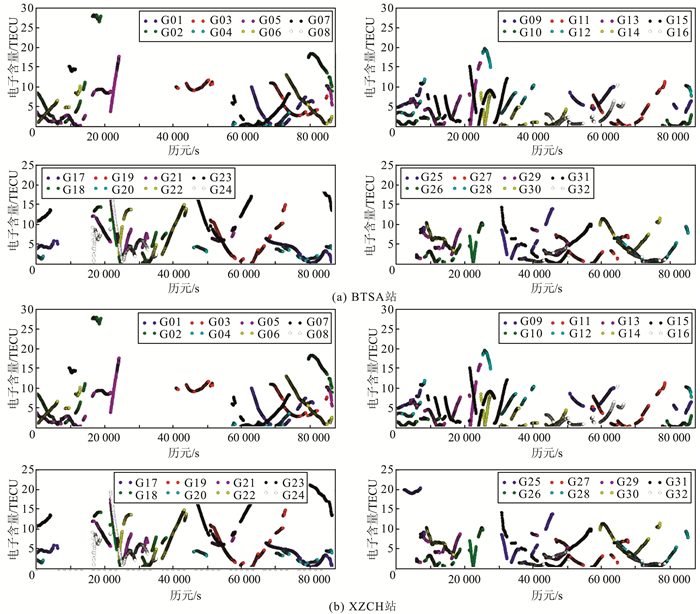 |
| 图 1 BTSA站与XZCH站所有卫星的逐历元的模型值与解算值的差的绝对值 Fig.1 Absolute Value of Difference Between Model Value and Solution Value of Epoch-by-Epoch for All Satellites of BTSA Station and XZCH Station |
分析各站结果可发现:①进行分段电离层多项式拟合时,每个时段内不能准确反映出电离层的跳变,引起图上的各个断点;②模型值与计算值之差的大小和卫星高度角有关,曲线呈现先降后升的趋势,说明在高度角较小的时候模型值与计算值差距较大,当高度角较大时差距小;③为提高模型精度可增加测站数量,但是效果不明显,可能是由于电离层延迟在高度角较低时估计精度不高所导致;④适当缩短时段长度可在一定程度上增加模型对于电离层变化的灵敏性;⑤实验的5个测站中,均方差的平均值达到7.7,其中,BTSA建模效果最好,均方差达到4.599,XZCH建模效果最差,均方差达到8.618;⑥天顶方向模型值与解算值差异(除个别卫星外)达到2 TECU左右。
JSXY站未参与建模,用该站PPP解算的数据与模型值作比较,以此来检验多项式建模的质量。图 2纵轴是测站所接收到的卫星在连续观测弧段中处于最大高度角时的PPP解算TECU值与模型值之差,横轴是卫星伪随机噪声码(pseudo random noise code, PRN),其中,没有08卫星的数据,故其值为0。观察图 2可发现大部分卫星处于4 TECU以内,只有06、09、12这3颗卫星的值在5 TECU左右。通过观察解算数据发现,当卫星高度角很低时,模型效果较差;当卫星高度角较高时,效果良好。其中多数卫星值都在1 TECU左右,甚至远小于1 TECU。经计算该数据的均方差为1.806,模型效果良好。
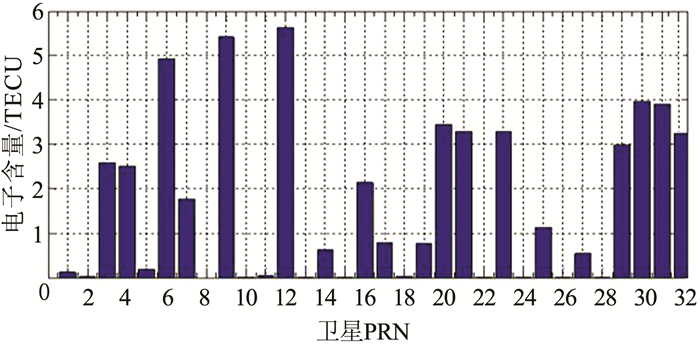 |
| 图 2 JSXY站各个卫星最大高度角时模型值与解算值的差值绝对值 Fig.2 Absolute Value of the Difference Between the Model Value and the Calculated Value at the Maximum Altitude Angle of Each Satellite of JSXY Station |
4 结束语
笔者推导了PPP算法解算电离层方法,并进行了多项式建模。PPP算法在一定程度上改善当前普遍使用方法容易受到多路径和观测噪声影响的缺陷。相对于双差电离层的方法,有效避免了模糊度无法固定而带来的影响。与GF组合的相位观测值提取的电离层相比,该方法充分利用可用信息,大量减少了待估参数的个数。在今后工作中,可以针对部分较易发生电离层异常的区域,使用PPP电离层观测值对该区域内的电离层作进一步的研究,为相关研究提供有价值的参考。通过实验证明了使用多项式拟合可以在测站天顶方向得到较好的电离层延迟值。构建的模型可以用于提高PPP收敛速度和辅助PPP模糊度固定。单频用户可利用附近基准站求解的电离层延迟进行电离层误差的削弱,得到更好的定位效果。将PPP电离层应用于普遍建设的CORS网中,在站坐标已知和模糊度固定的情况下,可以更好地约束电离层,获得更理想的效果,从而精化区域电离层模型。
| [1] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D].武汉: 武汉大学, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135460.htm
|
| [2] |
叶有龙, 刘宸, 刘长建. 利用标准单点定位技术评价电离层模型[J]. 测绘科学, 2017, 42(3): 126-131. |
| [3] |
Ciraolo L, Azpilicueta F, Brunini C, et al. Calibration Errors on Experimental Slant Total Electron Content (TEC) Determined with GPS[J]. Journal of Geodesy, 2007, 81(2): 111-120. DOI:10.1007/s00190-006-0093-1 |
| [4] |
Yuan Yunbin, Huo Xingliang, Ou Jikun. Models and Methods for Precise Determination of Ionospheric Delay Using GPS[J]. Progress in Natural Science:Materials International, 2007, 17(2): 187-196. DOI:10.1080/10020070612331343245 |
| [5] |
萧佐, 张东和. 通过GPS测量数据研究电离层电子总含量的逐日变化[J]. 空间科学学报, 2000, 20(2): 97-102. DOI:10.3969/j.issn.0254-6124.2000.02.001 |
| [6] |
常青, 张东和, 萧佐, 等. GPS系统硬件延迟估计方法及其在TEC计算中的应用[J]. 地球物理学报, 2001, 44(5): 596-601. DOI:10.3321/j.issn:0001-5733.2001.05.003 |
| [7] |
余涛, 万卫星, 刘立波, 等. 利用IGS数据分析全球TEC的周年和半年变化特性[J]. 地球物理学报, 2006, 49(4): 943-949. DOI:10.3321/j.issn:0001-5733.2006.04.003 |
| [8] |
Zhang Shoujian, Li Jiancheng, Zhao Lei. An Improved Method to Accelerate the Convergence of PPP-RTK with Sparse CORS Stations' Augmentation[C]. China Satellite Navigation Conference, Xi'an, 2015 http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=8474933
|
| [9] |
章红平, 平劲松, 朱文耀, 等. 电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1): 16-26. DOI:10.3969/j.issn.1000-8349.2006.01.002 |
| [10] |
孙伟, 乔炜, 周凯, 等. 基于地基GPS的武汉地区电离层TEC建模和变化分析[J]. 城市勘测, 2016(4): 114-118. DOI:10.3969/j.issn.1672-8262.2016.04.027 |
| [11] |
柳景斌, 王泽民, 章红平, 等. 几种地基GPS区域电离层TEC建模方法的比较及其一致性研究[J]. 武汉大学学报·信息科学版, 2008, 33(5): 479-483. |
| [12] |
李征航, 赵晓峰, 蔡昌盛. 全球定位系统(GPS)技术的最新进展第五讲利用双频GPS观测值建立电离层延迟模型[J]. 测绘信息与工程, 2003, 28(1): 41-44. DOI:10.3969/j.issn.1007-3817.2003.01.016 |
| [13] |
张宝成, 欧吉坤, 袁运斌, 等. 多参考站GPS网提取精密大气延迟[J]. 测绘学报, 2012, 41(4): 523-528. |
 2019, Vol. 44
2019, Vol. 44

