| BDS/GNSS虚拟基准站的网络RTK服务系统技术研究 |
2. 武汉大学卫星导航定位技术研究中心,湖北 武汉,430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
为了满足北斗卫星导航系统/全球导航卫星系统(Bei Dou navigation satellite system/global navigation satellite system, BDS/GNSS)基准站数据管理的相关规定,目前常用的网络实时动态(real-time kinematic, RTK)系统做法是在安全网络中部署内网,在内网中完成基准站网解算、区域误差模型生成、格网化的差分观测数据的生成。但是在较大范围内,为了保证流动站的定位精度,格网点间距通常定在5 km。在很多地区,由于原始GNSS观测数据的管理要求,难以满足构建合适密度格网的需求。姜益昊等[1]提出了一种GNSS基准站原始观测数据虚拟化算法,可以将GNSS原始观测数据包含的基准站坐标信息,在一定精度范围内进行等效平移,使新GNSS数据既可以继续作为参考基准使用,又不再与原始物理的基准墩和接收机天线位置存在对应关系。实测精密单点定位(precise point positioning, PPP)和RTK试验显示,算法在基准站平移30 m、300 m条件下,可达到1.5 mm以内的改正精度,该算法可以为大规模GNSS基准网数据虚拟化网络传输提供参考。
虚拟参考站技术具有覆盖范围广、定位精度高、可靠性高等优势,是当前广泛运用的GPS网络RTK技术。它利用连续运行基准站(continuously operating reference station, CORS)网络内基准站原始观测数据,实时解算各基线模糊度,建立区域大气误差模型,并在流动站附近创建一个虚拟参考站,通过内插等方法实现参考站数据的重建[2-10]。虚拟参考站的观测数据通常是在网络RTK服务中直接发送给流动站进行实时厘米级定位。朱照荣[11]利用城市CORS系统产生的虚拟基准站数据进行事后静态解算,可以获得与物理基准站同等的定位精度,验证了用虚拟参考站代替物理参考站的可行性。
综上所述,现有格网化虚拟参考站方法是通过生成密集的格网点参考站数据,基于在格网点一定距离范围内,所有流动站的改正数据相同的原理[12],为附近的流动站数据提供服务,从而解决服务器处理压力大的问题。此外,为了实现公网服务,满足国家对物理基准站数据的管控要求,必须把所有格网点数据(格网间距通常为1~5 km)通过单向光闸或者其他方式推送到公网,硬件成本大、实现难度高,对应的网络通信延迟加大。
因此,针对目前相关数据的管理规定和格网化参考站方法数据生成压力大、资源浪费严重的问题,本文提出了用虚拟基准站代替物理基准站,再进行基准站网数据处理、误差模型建立,最后向用户提供实时高精度定位服务。该方法从受控网络到公网之间传输的虚拟参考站数据的站点间距与物理基准站的站点间距保持一致(典型距离为50~70 km),数据量仅为传统的格网点数据量的1/100左右。虚拟基准站数据的获取有两种方式:(1)在物理基准站附近生成一个虚拟的基准站数据;(2)自定义网形的虚拟基准站观测值生成。
1 虚拟基准站观测值生成方法针对物理基准站原始观测数据只能在内网中传播的限制,可借助物理观测数据在一定精度范围内进行等效平移来生成虚拟观测数据。根据文献[1]中的算法,在获取物理基准站和虚拟基准站的精确坐标后,要完成观测数据的平移,需要实现几何信息的精确计算,并考虑平移过程中空间延迟差异以进行精确改正。因此,通过计算空间几何改正、电离层改正、对流层改正分量[13],再叠加到原始GNSS观测数据即可获取符合精度的虚拟观测数据。
1.1 基于物理基准站偏移的虚拟基准站生成方法由于虚拟观测值是通过物理基准站观测值添加改正得到的,其对流层改正数、电离层改正数、相对论效应、卫星的轨道差异等会受到物理站观测值的影响。此外,由于改正计算时还利用了广播星历,因此广播星历的误差也会影响虚拟观测值的精度。基于物理基准站偏移的虚拟基准站生成方法中,考虑到虚拟基准站的位置与物理基准站很近,因此认为物理基准站和虚拟基准站的大气、轨道误差是相同的,在生成中可以不进行相关误差改正,只需要将空间几何改正叠加到原始GNSS观测数据即可获取符合精度的虚拟观测数据。改正公式为:
| $ L_V^S=L_P^S+\Delta \rho_{r_v, r_p}^s $ | (1) |
式中,LVS为虚拟观测数据;LPS为物理观测数据;Δρrv, rps为空间几何改正。利用式(1)生成的虚拟观测值作为基准站进行组网解算时,应该注意以下几点:
1)生成虚拟基准站与物理基准站的偏移量一般为30~200 m。式(1)中可以看出,虚拟基准站与物理基准站的对流层改正数、电离层改正数、卫星轨道改正数与物理基准站完全一致,考虑到这些误差的空间相关性,保证误差的精度,因此不宜太远。
2)虚拟基准站与物理基准站观测值模糊度值完全相同,模糊度固定过程不受影响[14]。
综上所述,受控网络内的物理基准站观测值经过随机偏移后,只需经过空间几何改正即可形成虚拟基准站观测值,经过单向光闸到达公网后,进行网络RTK组网解算和产品服务[15]。
1.2 基于自定义网形的虚拟基准站生成方法基于自定义网络进行虚拟基准站生成的时候,虚拟基准站的位置可以任意设定,但是为了保持误差计算的准确性,一般要求虚拟基准站网形的站间距与物理基准站至少保持一致或者更加密集一些。与物理基准站偏移的虚拟基准站生成不同的是,自定义网形的虚拟基准站必须获得虚拟基准站处准确的相对大气改正。因此需要计算空间几何改正、电离层改正、对流层改正分量,再叠加到原始GNSS观测数据即可获取符合精度的虚拟观测数据。改正公式为:
| $ L_V^S=L_P^S+\Delta \rho_{r_v, r_p}^s+\Delta I_{r_v, r_p}^s+\Delta T_{r_v, r_p}^s $ | (2) |
式中,LVS为虚拟观测数据;LPS为物理观测数据;ΔIrs为电离层改正;ΔTrs为对流层改正;Δρsrv, rp为空间几何改正。
利用式(2)生成的虚拟观测值作为基准站进行组网解算时,应该注意以下几点:
1)误差来源以及影响大小:对流层改正数、电离层改正数获得是通过物理基准站网内插改正得到,其精度取决于内插模型的精度。由于相对论效应的影响,需考虑距离的影响。一般由于虚拟站与物理站较为接近,可以忽略。而对于卫星轨道误差,在虚拟观测站小于100 km的情况下,轨道误差基本上可以忽略。
2)对模糊度固定的影响:两者模糊度一致。在内插精度不够的情况下,如果影响模糊度固定,会对系统的服务和定位精度存在影响。如果不影响基准站网正确的固定模糊度,模糊度一旦固定正确,将重新计算电离层和对流层等误差改正数,将不会影响流动站的定位精度和性能。
3)误差值对基准站网的影响:基准站网的解算方程中,通过将物理基准站误差+内插误差统一当成误差值进行求解。具体求解时,由于在物理基准站附近完成虚拟基准站生成,二者对于基准站网数据的处理方式相同。
综上所述,受控网络内的物理基准站观测值经过网络RTK组网解算后,可以得到组网范围内的大气误差改正模型,根据自定义网形的虚拟基准站位置,进行大气误差改正和空间几何改正,即可形成虚拟基准站观测值,在经过单向光闸到达公网后,进行网络RTK组网解算和产品服务。
2 算例分析GNSS定位误差来源与空间地理位置特性相关,如电离层延迟在低纬度地区影响会更大,因此为了检验上述方法在不同地区的适应性,同时考虑到中国位于低纬度和中纬度区域,本文在武汉(中纬度)、广东(低纬度)两个区域开展了实验。
2.1 武汉区域实验本文利用武汉市周边的武汉大学科技园、蔡甸、阳逻3个自建基准站数据,使用自定义网形虚拟参考站生成方法,以45 km为间距生成了6个虚拟参考站。使用武汉大学研制的Power Network软件分别对物理基准站和虚拟基准站数据进行网络RTK解算和播发,通过功分器同时连接两台武汉攀达时空PD318接收机,进行物理基准站网和虚拟基准站网的RTK定位测试。基准站及流动站分布图分别如图 1、图 2所示。
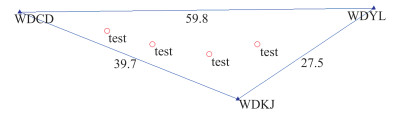 |
| 图 1 武汉算例物理基准站及流动站分布图 Fig.1 Distribution of Physical Reference Stations and Rover Stations in Wuhan |
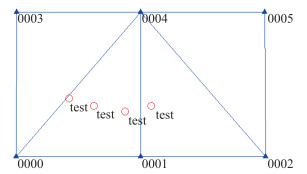 |
| 图 2 武汉算例虚拟基准站及流动站分布图 Fig.2 Distribution of Virtual Reference Stations and Rover Stations in Wuhan |
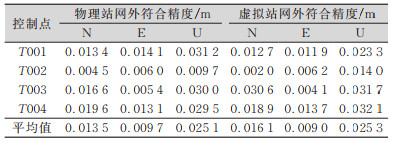
测试时间为2021年8月19日8时至8月20日8时,测试期间3个物理基准站的平均延时为0.15 s,虚拟基准站平均延时为0.20 s,同步延时量级相同,可以满足网络RTK时间同步要求。在网内选取4个点位T001~T004,连续采集了24 h的RTK定位结果,同时记录原始观测数据,使用PANDA软件计算得到参考值进行外符合精度分析,得到统计结果如表 1所示,其中T001点位误差序列如图 3所示。由结果可知,虚拟站网RTK定位精度与物理站网RTK定位精度基本一致。
| 表 1 武汉算例物理站网与虚拟站网RTK定位精度 Tab.1 External Coincidence Accuracy of RTK Positioning of Physical Station Network and Virtual Station Network in Wuhan Example |
 |
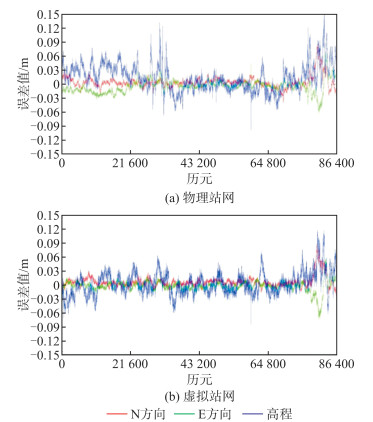 |
| 图 3 物理站网与虚拟站网的RTK定位结果误差序列 Fig.3 Error Sequence of RTK Positioning Results of Physical Station Network and Virtual Station Network |
2.2 广东区域实验
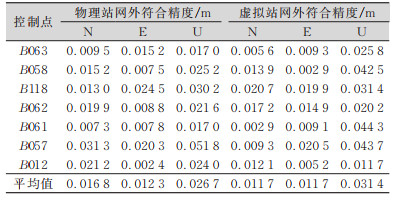
本文利用广东CORS现在的190余个基准站,使用文中介绍的基于物理基准站偏移的虚拟基准站生成方法,将基准站随机偏移10~30 m得到虚拟基准站数据,使用广东省国土资源测绘院与武汉大学共同开发的广东CORS发播平台分别对物理基准站和虚拟基准站数据进行网络RTK解算和播发(平均站间距为54.6 km)。在广东省范围内选取了7个控制点,分别使用物理基准站网和虚拟基准站网进行RTK测试,以控制点成果作为参考真值进行外符合精度统计,得到统计结果如表 2所示。由结果可得,虚拟站网RTK定位精度与物理站网水平相当,能够满足RTK定位精度指标。
| 表 2 广东算例物理站网与虚拟站网RTK定位精度 Tab.2 External Coincidence Accuracy of RTK Positioning of Physical Station Network and Virtual Station Network in Guangdong |
 |
3 结束语
本文针对现有网络RTK技术相关数据的管理规定和格网化参考站方法数据生成压力大、资源浪费严重的问题,提出了使用虚拟基准站数据代替物理基准站的服务方式,并提出了两种虚拟基准站的生成方法:①基于物理基准偏移的虚拟基准站生成方法,虚拟基准站的位置与物理基准站很近,在生成时只需要考虑空间几何改正;②基于自定义网形的虚拟基准站生成方法,虚拟基准站的位置可以自定义,在生成时需要考虑空间几何改正和大气误差改正。针对以上两种方法,本文在武汉、广东两个区域开展了实验分析,结果表明:以上两种方法生成的虚拟站网络RTK定位精度与物理站网水平相当,能满足RTK定位精度指标要求。
| [1] |
GNSS基准站原始观测数据的一种虚拟化算法[J]. 测绘地理信息, 2020, 45(5): 29-34. |
| [2] |
Alves D B M, Monico J F G. GPS/VRS Positioning Using Atmospheric Modeling[J]. GPS Solutions, 2011, 15(3): 253-261. DOI:10.1007/s10291-010-0187-3 |
| [3] |
向涛, 郭际明, 王磊, 等. GPS/VRS关键技术研究及其定位应用[C]. 第四届中国卫星导航学术年会, 武汉, 2013.
|
| [4] |
张晶晶. BDS网络RTK虚拟参考站数据生成的算法研究[D]. 北京: 中国测绘科学研究院, 2014.
|
| [5] |
唐卫明. 大范围长距离GNSS网络RTK技术研究[D]. 武汉: 武汉大学, 2006.
|
| [6] |
陈新东. GPS_VRS虚拟观测值生成算法研究[D]. 南昌: 南昌大学, 2019.
|
| [7] |
杨聪. GPS虚拟参考站算法研究及软件开发[D]. 北京: 清华大学, 2010.
|
| [8] |
基于VRS的GPS虚拟相位观测值生成算法研究[J]. 大地测量与地球动力学, 2009, 29(1): 123-126. |
| [9] |
网络RTK虚拟参考站的数学模型研究[J]. 舰船电子工程, 2018, 38(8): 42-45. |
| [10] |
朱超. 一种新的GPS/VRS虚拟观测值生成算法[C]. 第19届华东六省一市测绘学会学术交流会暨2017年海峡两岸测绘技术交流与学术研讨会, 济南, 2017.
|
| [11] |
朱照荣. 基于CORS系统的虚拟基准站数据应用研究[C]. 全国工程测量2012年技术研讨交流会, 沈阳, 2012.
|
| [12] |
格网化高精度卫星导航定位服务方法[J]. 测绘科学, 2020, 45(11): 53-58. |
| [13] |
GPS/VRS对流层延迟误差内插模型研究[J]. 测绘与空间地理信息, 2013, 36(2): 127-129. |
| [14] |
三步法确定网络RTK基准站双差模糊度[J]. 武汉大学学报·信息科学版, 2007, 32(4): 305-308. |
| [15] |
张熙. 多星座CORS混合观测网络实时位置服务关键技术研究[D]. 成都: 西南交通大学, 2016.
|
 2022, Vol. 47
2022, Vol. 47


