| GNSS基准站原始观测数据的一种虚拟化算法 |
2. 武汉大学卫星导航定位技术研究中心, 湖北 武汉, 430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
近年来,我国各省市区域GNSS(global navigation satellite system,全球导航卫星系统)地基增强系统蓬勃发展,同时随着我国“陆态网络”、“国家GNSS连续运行基准站网”等国家基础设施的建设,GNSS基准站网已基本覆盖了我国大部分国土面积。由中国兵器承担建设,目前由千寻位置网络有限公司具体运营的北斗地基增强系统,建设了全国2 000多个以北斗为主、兼容其他GNSS(BDS/GNSS)的基准站网络。
由于GNSS基准站原始观测数据与天线物理基准墩对应,在获取基准站原始观测数据后,可以精确解算出在特定参考坐标框架下的精确坐标。只要获取3个及以上基准站精确坐标,就能以基准墩所在地图或者影像进行精确标定。因此我国测绘法规定3个以上的原始GNSS观测数据属于秘密资料。目前类似于千寻位置网络公司运营的BDS/GNSS地基增强服务网络,以及各省市的BDS/GNSS地基增强参考站网络原始数据,不仅要在网上传播,还要服务于网络用户。但这些数据根据我国测绘法均不能在公网上传输,需要大量的专网传输,这不仅会增加成本,而且在特定基准站实现起来非常困难。在这种情况下,本文针对性地提出一种对数据进行平移虚拟化的算法,在不损失GNSS观测数据空间信息精度的条件下,使观测数据与基准站基准墩和天线彻底分离,使虚拟的GNSS数据不再具有实际的物理基准站特性,但仍然可作为RTK(real time kinematic)和网络RTK、广域精密定位系统的参考站使用,并且保持其作为参考站的属性,可适用于mm级大地测量基准以及地球动力学研究。
1 虚拟参考站观测数据生成将GNSS原始数据包含的基准站坐标信息平移,且保证GNSS数据的有效性,则要实现空间几何信息的精确计算,并考虑平移过程中空间传播延迟差异,并作精确改正[1]。BDS/GNSS的伪距和载波的观测方程为[2-4]:
| $ \begin{array}{c} p_{r, j}^s(t) = \rho _r^s(t, t - \tau _r^s) + T_r^s(t) + \\ c[{\rm{d}}{t_r}(t) + d_{r, j}^s(t) + \Delta d_{r, j}^s(t)] - \\ c[{\rm{d}}{t^s}(t - \tau _r^s) - d_j^s(t - \tau _r^s)] + \\ \mu _j^sI_r^s(t) + e_{r, j}^s(t) \end{array} $ | (1) |
| $ \begin{array}{c} \varphi _{r, j}^s(t) = \rho _r^s(t, t - \tau _r^s) + T_r^s(t) + \\ c[{\rm{d}}{t_r}(t) + \delta _{r, j}^s(t) + \Delta \delta _{r, j}^s(t)] - \\ c[{\rm{d}}{t^s}(t - \tau _r^s) - \delta _j^s(t - \tau _r^s)] + \\ \mu _j^sI_r^s(t) + \lambda _j^sN_{r, j}^s + \varepsilon _{r, j}^s(t) \end{array} $ | (2) |
式(1)与式(2)中,pr, js为伪距观测值(m);φr, js为载波相位观测值(m);ρrs为卫星-测站间的几何间距(m);τrs为信号传输时间(s);Trs为对流层延迟(m);c为真空中的光速(m/s);dtr为接收机钟差(s);dts为卫星钟差(s);dr, js为接收机端码伪距硬件延迟(s);δr, js为接收机端相位硬件延迟(s);Δdr, js为码通道间偏差(s);Δδr, js为相位通道间偏差(s);djs为卫星端码伪距硬件延迟(s);δjs为卫星端相位硬件延迟(s);μjs为电离层系数;Irs为电离层延迟(m);λjs为载波相位波长(m);Nr, js为载波相位模糊度(周);er, js为码伪距随机噪声(m);εr, js为载波相位随机噪声(m)。
将基准站平移虚拟化,主要需考虑空间几何以及参考地点变化引起的传播路径变化,因此只需要改变观测方程中卫星-基准站间的几何间距ρrs、电离层延迟Irs以及对流层延迟Trs等3个方面,其他物理量仍然保持不变[5, 6]。分别从空间几何改正、电离层和对流层传播路径误差改正3个部分简要介绍算法原理。
1) 空间几何改正。首先获取GNSS导航卫星的广播星历,以及基准站精确的参考坐标,并计算广播星历中各导航系统卫星和物理基准站之间的距离ρr1s。设定虚拟参考站(图 1)与物理基准站之间的距离关系,这样就能获得虚拟站点的精确坐标。然后进一步利用同一组GNSS广播星历中卫星与虚拟参考站之间的距离ρr2s。通过互差ρr2s-ρr1s得到虚拟参考站和物理基准站与广播星历之间距离的差值,即每颗卫星空间几何改正。
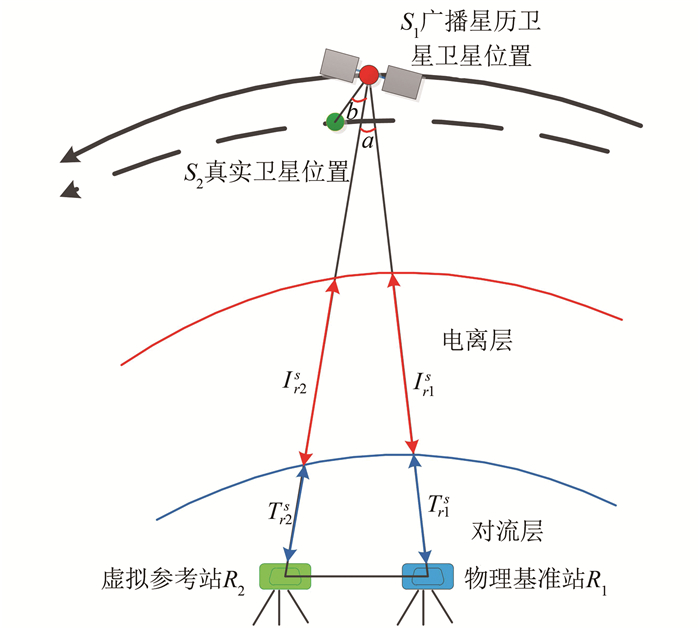 |
| 图 1 虚拟参考站生成原理示意图 Fig.1 Diagram of Virtual Reference Station Generation |
2) 电离层延迟改正。为了使虚拟参考站GNSS观测数据尽可能地接近实测观测数据效果,需要对GNSS各卫星信号到达虚拟参考站与物理基准站位置之间传播路径上的延迟进行改正。传播路径延迟改正分为电离层和对流层改正。在这种情况下,电离层改正总量差异比较小,采用广播星历中的电离层参数就可以改正到60%以上,采用欧洲定轨中心(conter for orbit determination in Europe, CODE)的球谐系数模型改正可以达到90%左右[7]。分别计算得到卫星到物理基准站和虚拟参考站的电离层延迟Ir1s和Ir2s,作差可以得到Ir2s-Ir1s,即为电离层延迟改正。
3) 对流层延迟改正。GNSS观测中,天顶对流层延迟通常被分为天顶静力学延迟(zenith hydrostatic delay,ZHD)和天顶非静力学延迟(zenith wet delay,ZWD)两部分来处理,总的天顶对流层延迟大约为2.3 m[8]。现有模型可以改正90%~95%[9],由于虚拟参考站与物理基准站基线一般设置较短,天顶对流层延迟在空间尺度上与经度和纬度具有相关性、与高程强相关[10, 11]。因此总体而言,只要高程变化平稳,对流层延迟变化就不会很大。与电离层类似,分别计算得到卫星到物理基准站和虚拟参考站的天顶对流层延迟Tr1s和Tr2s,作差可以得到Tr2s-Tr1s,即为天顶对流层延迟改正。
综合几何改正、电离层和对流层改正,就可以得到虚拟参考站观测值所有改正,叠加到原始观测量即可获得虚拟观测值。相关原理和网络RTK里基本一致,只是这里仅采用经验误差模型,而且虚拟的基线相对较短。本文不只是要求精度满足cm级的动态定位要求,而是要求基本不改变原始观测值的物理特性,精细改正达到1.5 mm以内。
2 系统误差理论分析 2.1 卫星轨道误差投影分析考虑到卫星广播星历存在误差[12-14],即使采用同一组广播星历,随着地面虚拟参考站与物理基准站之间的基线长度的增加,星历误差仍会导致虚拟观测值误差有一定的增加。参考图 1,假设广播星历的位置为S1,真实卫星轨道上卫星位置为S2,位置误差矢量与卫星与虚拟参考站星站方向之间的夹角为b,卫星到物理基准站以及卫星到虚拟参考站之间的夹角为a,则误差矢量在实测观测数据和虚拟观测数据上的投影可表示为:
| $ \delta _{\rho 2}^{\rho 1} = \delta _{{S_2}}^{{S_1}}\left[ {{\rm{cos}}\left( {a + b} \right) - \cos \left( a \right)} \right] $ | (3) |
式中,δs2s1为卫星广播星历的误差;δρ2ρ1为广播星历误差,利用三角函数求差公式得:
| $ \delta _{\rho 2}^{\rho 1} = \delta _{{S_2}}^{{S_1}}\left( { - 2} \right)\sin \left[ {\left( {2a + b} \right)/2} \right]\sin \left( {b/2} \right) $ | (4) |
化简得:
| $ \delta _{\rho 2}^{\rho 1} = \delta _{{S_2}}^{{S_1}}\left( { - 2} \right)\sin \left( {a + b/2} \right)\sin \left( {b/2} \right) $ | (5) |
综上所述,由于卫星轨道高度一般都大于20 000 km[14, 15],虚拟基线一般要求要小于10 km,因此角度b足够小,则:
| $ \sin \left( {b/2} \right) \approx D_{r2}^{r1}/2{\rho _1} $ | (6) |
式中, Dr2r1为基线向量长度;ρ1为广播星历卫星到基准站之间得距离。则:
| $ \delta _{\rho 2}^{\rho 1} = \delta _{{S_2}}^{{S_1}}\left( { - 1} \right)\sin \left( {a + b/2} \right)D_{r2}^{r1}/{\rho _1} $ | (7) |
鉴于sin(a+b/2)≤1,则仅考虑误差绝对值大小,则有:
| $ \delta _{\rho 2}^{\rho 1} = \delta _{{S_2}}^{{S_1}}\;D_{r2}^{r1}/{\rho _1} $ | (8) |
根据上式可知,考虑目前卫星轨道通常优于1 m[16-20],星地几何距离通常大于20 000 km,在基线分别为30 m、300 m、1 km和10 km,对应的卫星轨道误差影响分别小于:0.0015 mm、0.015 mm、0.05 mm和0.5 mm。
2.2 电离层延迟改正误差分析为了考查电离层可能的改正误差,本文分析了全球电离层在基线条件下总电离层延迟差异。首先利用CODE的全球电离层格网模型来模拟全球电子含量总的变化趋势,将格网在水平方向平移30 m、300 m、1 km、10 km得到4类基线的电离层延迟差异,将每类基线的所有可视卫星L1频点电离层差异绝对值取平均,得到4类基线电离层误差的全球分布图(图 2)。
 |
| 图 2 不同虚拟基线长度(30 m、300 m、1 km、10 km)电离层延迟偏差分布图 Fig.2 Distribution of Ionospheric Delay Deviations for Different Virtual Baseline (30 m, 300 m, 1 km, 10 km) |
从图 2中可以看出, 30 m和300 m基线的总电离层偏差均小于1 mm,1 km基线在2 mm量级,而10 km的基线在2 cm范围以内。所以即使不考虑电离层误差改正,30 m和300 m的虚拟基线电离层误差也会优于1 mm。考虑到广播星历改正可以改正50%以上,所以即使1 km的基线一般也在1 mm以内。当然在太阳活跃时期,会有一定的增加,但不至于量级上有特别大的变化。
2.3 对流层改正误差分析为了考查对流层可能的改正误差,本文利用Saastamoinen模型,经、纬度方向每30弧秒取一个网格点,同时参考高程模型采用美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)提供的ETOPO1全球基岩高程网格数据,计算出全球天顶对流层延迟分布Tr1s。随后将所有网格点在水平方向平移一个基线长度的距离,计算全球天顶对流层延迟分布Tr2s,作差即可得到对应基线条件下的全球天顶对流层延迟改正量Tr2s-Tr1s。30 m、300 m、1 km和10 km基线下天顶对流层误差的全球分布图如图 3所示。
 |
| 图 3 不同虚拟基线长度(30 m、300 m、1 km、10 km)天顶对流层延迟偏差分布图 Fig.3 Distribution of Zenith Tropospheric Delay Deviations for Different Virtual Baseline (30 m, 300 m, 1 km, 10 km) |
从图 3中可以看出, 30 m和300 m基线的天顶对流层偏差均远小于1 mm,大部分地区的1 km基线天顶对流层偏差为1 mm量级,10 km基线在1 cm范围以内。所以即使不考虑对流层误差改正,30 m和300 m的虚拟基线天顶对流层误差也会优于1 mm。考虑到现有模型改正可以达90%以上,所以即使10 km的基线一般也可以将误差控制在1 mm以内。当然在高程变化剧烈的地区会有一定的增加[21],但也可以通过恰当地选取虚拟站位置来改善。
3 实测数据验证本文利用BDS和GPS原始观测数据进行了虚拟化算法有效性验证。实测数据验证采用了PPP(precise point positioning)和RTK两种方案。
1) PPP方案中,本文选取了全球范围内20个IGS基准站2020-03-01的观测数据进行PPP解算,对原始观测量进行虚拟化平移,平移量分别随机向东或者向南平移30 m、300 m、1 km、10 km,获得新的虚拟参考站及对应观测数据,然后利用PPP分别单独解算原始基准站数据和虚拟参考站数据。通过对比两类数据实时动态定位结果差异,查看其可替代性。
对于PPP,绘制出虚拟测站和参考站动态定位结果差异(下称“定位偏差”)图(图 4)及其均方根误差(root mean square,RMS)柱状图(图 5);定位偏差及定位偏差RMS按下式计算:
| $ d_{i, 0}=\left(X_{i}^{\prime}-X_{0}\right)^{2}+\left(Y_{i}^{\prime}-Y_{0}\right)^{2}+\left(Z_{i}^{\prime}-Z_{0}\right)^{2} $ | (9) |
| $ \begin{array}{*{20}{c}} {{d_{i, n}} = {{\left( {x_{i, n}^\prime - {x_{i, 0}}} \right)}^2} + {{\left( {y_{i, n}^\prime - {y_{i, 0}}} \right)}^2} + }\\ {{{\left( {z_{i, n}^\prime - {z_{i, 0}}} \right)}^2}} \end{array} $ | (10) |
| $ \Delta {d_{i, n}} = {d_{i, n}} - {d_{i, 0}} $ | (11) |
| $ {\rm{RM}}{{\rm{S}}_i} = \sqrt {\frac{{\sum\limits_{n = 1}^N \Delta d_{i, n}^2}}{N}} $ | (12) |
 |
| 图 4 NIST基准站定位偏差序列图 Fig.4 Positioning Deviation Sequence Diagram of NIST |
 |
| 图 5 各测站定位偏差RMS柱状图 Fig.5 RMS Histograms of Positioning Deviation |
式中,(Xi, 0,Yi, 0,Zi, 0)为第i测站基准站的真实坐标;(X′i, 0,Y′i, 0,Z′i, 0)第i测站虚拟站的真实坐标;(xi, 0,yi, 0,zi, 0)为第i测站基准站第n历元的解算坐标;(x′i, 0,y′i, 0,z′i, 0)第i测站虚拟站第n历元的解算坐标;Δdi, n为第i测站第n历元的定位偏差;N为历元总数;RMSi为第i测站定位偏差均方根误差。
2) RTK方案中,选取了武汉相距15.5 km的两个基准站进行了验证。其中一个基站作为基准站,一个作为流动站,给出流动站以基准站原始数据和分别虚拟30 m、300 m、1 km和10 km作为参考获得的动态定位结果的差异。图 6给出了流动站的定位差异ERROR的序列图。
| $ {\rm{ERROR}} = \left[ {\begin{array}{*{20}{l}} {X_{{\rm{RTK}}}^\prime - X_{{\rm{RTK}}}^0}\\ {Y_{{\rm{RTK}}}^\prime - Y_{{\rm{RTK}}}^0}\\ {Z_{{\rm{RTK}}}^\prime - Z_{{\rm{RTK}}}^0} \end{array}} \right] $ | (13) |
 |
| 图 6 RTK定位差异序列图 Fig.6 Error Sequence Diagram of RTK Positioning |
式中,(X′RTK,Y′RTK,Z′RTK)为虚拟站作基准站的用户站解算坐标;(XRTK0,YRTK0,ZRTK0)为原始站作基准站的用户站解算坐标。
限于篇幅,此处只给出NIST测站的PPP定位偏差序列图以及平移30 m、300 m、1 km、10 km的RTK定位偏差序列图。
通过定位偏差及其RMS序列图来看,对于PPP,虚拟化平移30 m和300 m时可以保证误差在1 mm以内,平移1 km的误差基本在1 mm以内,平移10 km可以保证误差在1.5 mm以内;对于RTK,平移30 m时误差可以保证在1 mm以内,平移300 m误差在1.5 mm以内,平移1 km误差基本在2 mm以内,平移10 km误差在5 mm以内。
4 结束语本文提出了一种基于广播星历和经验电离层、对流层模型的BDS/GNSS物理基站虚拟化的算法,文中基于理论分析和实测数据检验可知,本方法可以根据需求将基准站观测数据虚拟化平移30 m,相关虚拟化误差小于1 mm,平移300 m则误差小于1.5 mm。该方法完全保留了BDS/GNSS原始数据的其他物理特征,仍然适用于和原有物理基准站一致的高精度应用目标,如大地测量基准、地球动力学研究等,同样可适用于各省市的BDS/GNSS地基增强系统基准站网数据的虚拟化传输。
| [1] |
Wanninger L. Virtual Reference Stations (VRS)[J]. GPS Solutions, 2003, 7(2): 143-144. DOI:10.1007/s10291-003-0060-8 |
| [2] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D].武汉: 武汉大学, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135460.htm
|
| [3] |
叶世榕. GPS非差相位精密单点定位理论与实现[D].武汉: 武汉大学, 2002 http://d.wanfangdata.com.cn/Thesis/Y557920
|
| [4] |
李盼. GNSS精密单点定位模糊度快速固定技术和方法研究[D].武汉: 武汉大学, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10486-1016113506.htm
|
| [5] |
张晶晶. BDS网络RTK虚拟参考站数据生成的算法研究[D].北京: 中国测绘科学研究院, 2014 http://cdmd.cnki.com.cn/Article/CDMD-86001-1014330454.htm
|
| [6] |
杨小军.虚拟参考站(VRS)技术与差分改正信息的研究[D].成都: 西南交通大学, 2005 http://d.wanfangdata.com.cn/Thesis/Y751770
|
| [7] |
张强, 赵齐乐. 武汉大学IGS电离层分析中心全球电离层产品精度评估与分析[J]. 地球物理学报, 2019, 62(12): 4493-4505. |
| [8] |
李征航, 黄劲松. GPS测量与数据处理(第二版)[M]. 武汉: 武汉大学出版社, 2010.
|
| [9] |
殷海涛, 黄丁发, 熊永良, 等. GPS信号对流层延迟改正新模型研究[J]. 武汉大学学报·信息科学版, 2007, 32(5): 454-457. |
| [10] |
尹晖, 费添豪. 区域天顶对流层延迟时空变化特性及其建模研究[J]. 测绘工程, 2017, 26(11): 1-5. |
| [11] |
赵齐乐, 李晓涛, 耿江辉. GPS/GLONASS/BeiDou/Galileo PPP快速模糊度固定[J]. 测绘地理信息, 2018, 43(3): 1-8. |
| [12] |
刘经南, 曾旭平, 夏林元, 等. 导航卫星自主定轨的算法研究及模拟结果[J]. 武汉大学学报·信息科学版, 2004, 29(12): 1040-1044. |
| [13] |
张晓旭.广播星历误差和电离层矫正精度监测与评估[D].石家庄: 河北科技大学, 2019 http://cdmd.cnki.com.cn/Article/CDMD-10082-1019014231.htm
|
| [14] |
庄辑. 全球卫星定位系统(GPS)简介[J]. 珠江水运, 2009(5): 63. |
| [15] |
徐磊, 杨旭海, 弓剑军, 等. 卫星共视与基线长度及卫星高度关系的研究[J]. 时间频率学报, 2019, 42(3): 256-265. |
| [16] |
夏博洋.加速度计数据辅助星载GPS自主定轨方法研究[D].武汉: 武汉大学, 2017
|
| [17] |
张强.采用GPS与北斗的低轨卫星及其编队精密定轨关键技术研究[D].武汉: 武汉大学, 2018 http://cdmd.cnki.com.cn/Article/CDMD-10486-1019017408.htm
|
| [18] |
王乐. BDS卫星实时精密定轨及低轨卫星增强技术研究[D].西安: 长安大学, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10710-1018791476.htm
|
| [19] |
范磊.北斗/GNSS实时高效精密定轨及频间时钟偏差特性研究[D].武汉: 武汉大学, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10486-1018031371.htm
|
| [20] |
朱永兴, 冯来平, 贾小林, 等. 北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377-383. |
| [21] |
刘立龙, 陈雨田, 黎峻宇, 等. 活跃期区域电离层总电子短期预报及适用性分析[J]. 武汉大学学报·信息科学版, 2019, 44(12): 1757-1764. |
 2020, Vol. 45
2020, Vol. 45

