| 北斗实时精密单点定位与精度分析 |
2. 武汉大学卫星导航定位技术研究中心,湖北 武汉,430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
精密单点定位(precise point positioning,PPP)由美国喷气推进实验室(Jet Propulsion Laboratory,JPL)的Zumberge等人提出,该技术利用国际GNSS服务组织(International Global Navigation Satellite System Service, IGS)提供的精密轨道和钟差产品,采用相位观测值单台接收机便可实现高精度导航定位服务[1]。近年来,实时PPP成为国内外研究的热点,被广泛应用于实时导航与位置服务[2]。2012年底,我国北斗卫星导航系统(BeiDou navigation satellite system,BDS)实现了对亚太区域的定位服务,是继全球定位系统(global positioning system,GPS)和全球卫星导航系统(global navigation satellite system,GLONASS)之后第3个可独立运行的卫星导航定位系统。计划在2020年,BDS可在全球范围内全天候为各类用户提供高精度、高可靠的导航定位、授时服务,并具短报文通信功能[3]。为实现北斗实时精密定位服务,国内外开展了北斗广域实时精密单点定位服务应用研究,本文基于武汉大学卫星导航定位技术研究中心播发的北斗实时精密轨道和钟差产品,采用北斗实时双频手持机,进行实时PPP定位,并对定位的收敛时间和精度进行分析。
1 精密单点定位模型为消除电离层延迟对定位的影响,双频PPP采用无电离层组合观测值(LC组合观测值),其观测方程可表示为:
| $ \left\{ \begin{array}{l} {l_p} = \rho + c\left( {{\rm{d}}t - {\rm{d}}T} \right) + m \times {\rm{ZTD}} + {\varepsilon _p}\\ {l_\varphi } = \rho + c\left( {{\rm{d}}t - {\rm{d}}T} \right) + {\rm{amb}} + m \times {\rm{ZTD}} + {\varepsilon _\varphi } \end{array} \right. $ | (1) |
式中, lp和lφ分别为无电离层组合伪距和相位观测值;dt和dT分别为接收机和卫星钟差;c为真空中的光速;amb为无电离层组合模糊度;m为对流层投影函数;ZTD为天顶方向对流层延迟;εp和εφ分别为观测噪声和多路径误差;ρ为测站(Xr, Yr, Zr)和卫星(Xs, Ys, Zs)间的几何距离,包括相对论效应、固体潮、天线相位中心及相位绕转等误差,即
| $ \rho = \sqrt {{{\left( {{X_r} - {X_s}} \right)}^2} + {{\left( {{Y_r} - {Y_s}} \right)}^2} + {{\left( {{Z_r} - {Z_s}} \right)}^2}} $ | (2) |
将式(2)线性化,则有误差方程:
| $ V = \mathit{\boldsymbol{A}}\delta \mathit{\boldsymbol{X}} + \mathit{\boldsymbol{W}} $ | (3) |
式中,A为系数矩阵;δX为待估计参数,包括测站三维坐标、接收机钟差、无电离层组合模糊度及对流层天顶湿延迟;W为常数项矩阵。
2 北斗精密单点定位策略由于BDS空间星座的不同特性,与GPS的PPP数据处理比较,需要考虑观测值定权策略、与卫星姿态有关的误差模型、天线相位中心模型等问题。
1) 观测值定权策略。GPS精密单点定位中,通常依据卫星高度角来确定不同卫星观测值间的权比关系。但是BDS卫星星座包括地球静止轨道(geostationary earth orbit,GEO)卫星、倾斜地球同步轨道(inclined geosynchronous satellite orbit,IGSO)卫星和中地球轨道(medium earth orbit, MEO)卫星[4],GEO、IGSO和MEO轨道与钟差的精度不一致,因此采用与GPS一样的定权策略不合理,本文根据不同卫星星座分别确定其相应的权比关系[5]。
2) 与卫星姿态有关的误差改正。BDS卫星与GPS卫星姿态控制模式不同,北斗IGSO、MEO卫星采用了动态偏航和零偏航两种控制模式,而GEO卫星全弧段采用零偏航控制模式[6],控制模式的不同会影响到天线相位中心改正和天线相位缠绕改正的不同,需要针对不同的姿态模型进行相应的改正。
3) 天线相位中心模型。北斗系统天线相位中心改正目前主要有3种策略:①北斗卫星制造商提供的改正参数仅改正天线相位中心偏差(phase center offset,PCO)部分,不改正天线相位中心变化(phase center offset variation,PCV);②国际多模GNSS实验工程(multi-GNSS experiment,MGEX)采用的方法也仅改正PCO;③欧空局(European Space Agency,ESA)采用的方法同时改正PCV和PCO[7]。由于本文北斗实时轨道及钟差解算时采用了ESA提供的天线相位中心模型改正,因此,实时PPP中也采用该天线相位中心改正模型。
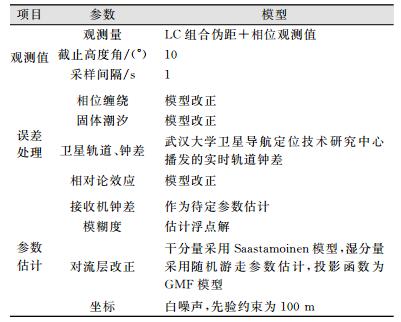
通过无电离层组合观测值消除电离层一阶项影响后,相对论效应、地球固体潮和相位绕转等误差采用IGS提供的高精度模型进行改正,天顶对流层延迟干分量用Saastamoinen模型[8]改正,湿分量采用随机游走方法进行估计,对流层投影函数采用GMF(graphical modeling framework)模型,因此,PPP待估参数包括测站三维坐标、接收机钟差、模糊度以及天顶对流层湿延迟。本文在数据预处理阶段首先进行钟跳探测与修复,然后联合使用Geometry-Free与Melbourne-Wübbena组合观测值探测周跳[9]。具体数据处理策略如表 1所示。其中,GMF模型提供了图形化编辑器的开发环境和运行时的框架。
| 表 1 北斗实时PPP数据处理策略 Table 1 Strategy of the BDS Real-Time PPP Data Processing |
 |
3 测试及精度分析
本文采用实测数据对北斗PPP定位进行分析,测试地点在武汉大学教学实验大楼,所用手持机为攀达时空北斗双频手持机,通过连接转发器接收北斗观测信号。测试时,采用内置天线和外置天线两种方式,2015年6月26日采用内置天线,静态观测时间约为8 h 34 min;2015年8月2日采用外置天线,静态观测时间约为8 h 6 min。手持机所测的真值坐标通过事后实时动态测量(real-time kinematic, RTK)解算的方法获得,误差时间序列如图 1所示, 其中,N、E、U构成以测量点为原点的站心坐标系,N表示北方向,E表示东方向,U表示天顶方向。
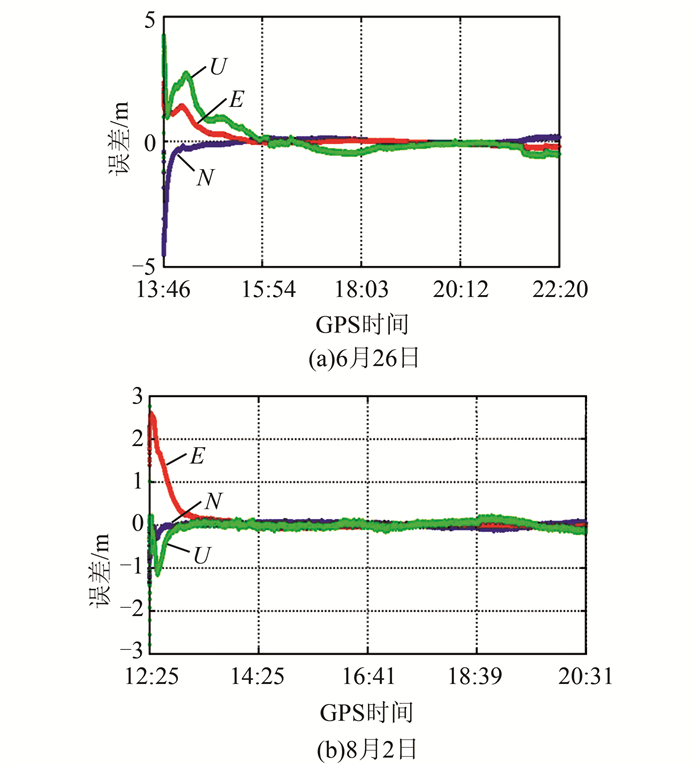 |
| 图 1 双频实时PPP误差时间序列图 Figure 1 Time Series of the Error for BDS Dual Frequency Real-Time PPP |
分析图 1可以得出:①以平面收敛精度优于5 dm、高程精度优于1 m为标准,6月26日的收敛时间约为70 min,8月2日约为30 min;②若平面优于3 dm、高程优于5 dm,则6月26日的收敛时间约为100 min,8月2日约为40 min;③当平面优于2 dm、高程优于2 dm时,则6月26日的收敛时间约为120 min,8月2日约为50 min。从以上分析可以看出,8月2日的收敛时间明显小于6月26日,这是因为6月26日测试时使用内置天线,而8月2日使用了外置天线,观测值数据质量更好。另外,虽然大部分时间北斗卫星数多于GPS,但由于目前北斗的MEO卫星数较少,总体上北斗的位置精度强弱度(position dilution of precision, PDOP)反而不如GPS的PDOP。此外,北斗几何图形变化不如GPS星座的显著。当前由于北斗跟踪站数量有限,北斗精密轨道的精度相对较低,从而导致北斗实时PPP的收敛时间要比GPS收敛时间(约0.5 h[10])长。
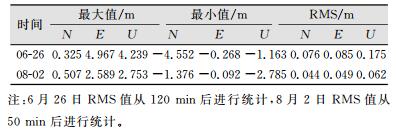
单北斗PPP的定位精度如表 2所示。可以看出,基于北斗系统的实时动态PPP收敛后可以达到分米至亚分米级的定位精度,与GPS实时动态PPP定位精度相当。比较分析测试结果的均方根(root mean square,RMS)值发现,8月2日测试结果明显优于6月26日,这同样是因为8月2日测试使用了外置天线,观测值质量较好的结果。另外,北分量的精度要高于东分量,这是因为实时PPP中模糊度采用浮点解,未将其固定为整数[11]。
| 表 2 定位结果统计 Table 2 Statistics of the Positioning Results |
 |
4 结束语
本文基于武汉大学卫星导航定位技术研究中心播发的实时轨道和钟差产品,采用攀达时空北斗双频手持机进行实时精密单点定位测试,对其收敛时间和定位精度进行分析。从测试结果中可以看出,北斗双频手持机实时PPP可以达到分米级甚至是厘米级的动态定位精度,与GPS实时PPP的定位精度相当。当前由于北斗的全球跟踪站有限,精密轨道和钟差精度不如GPS等原因,北斗的收敛时间较GPS长约0.5 h。另外,使用外置天线的北斗手持机在收敛时间和定位精度方面都要优于使用内置天线的手持机。
| [1] | Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 005–5 017 DOI: 10.1029/96JB03860 |
| [2] | 施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 42(6): 854–861 |
| [3] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6 |
| [4] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72–81 |
| [5] |
易文婷. 多系统GNSS组合精密单点定位快速收敛与非差模糊度固定方法研究[D]. 武汉: 武汉大学, 2015 |
| [6] | 毛悦, 宋小勇, 王维, 等. 北斗IGSO/MEO卫星姿态控制及光压差异分析[J]. 测绘科学, 2015, 40(8): 129–134 |
| [7] | 黄观文, 张睿, 张勤, 等. BDS卫星天线相位中心改正模型比较[J]. 大地测量与地球动力学, 2015, 35(4): 658–661 |
| [8] | Saastamoinen J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[J]. Use of Artificial Satellites for Geodesy, 1972, 15(6): 247–251 |
| [9] | 李盼, 郭斐, 刘季. 实时精密单点定位中的数据预处理研究[J]. 测绘地理信息, 2012, 37(5): 29–32 |
| [10] | 张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250–256 DOI: 10.11947/j.AGCS.2015.20130771 |
| [11] | Blewitt G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2 000 km[J]. Journal of Geophysical Research: Atmospheres, 1989, 94(B8): 10.187–10.203 DOI: 10.1029/JB094iB08p10187 |
 2017, Vol. 42
2017, Vol. 42

