| GIS支持下的辽宁省海岸线分形特征研究 | [PDF全文] |
海岸线作为海陆分界线,是典型的地理分形事物。Mandelbort[1]通过对海岸线的深入观察和研究,提出海岸线的长度虽随量测尺度大小而变化,但分维值不变,其值域介于1~2之间。分维值越大,海岸线就愈曲折和复杂[2-4]。此后,国内外不少学者利用量规法(折线法)[5]、网格法(盒子法)[6]等对不同国家或区域海岸线的分形维数进行了研究[7-17]。
自《海域法》出台后,海岸线的位置和长度等地理基础信息已成为沿海各级政府和有关部门进行海洋综合管理的必要数据。由于海岸线的长度因测量尺度不同,所测得的同一段海岸线长度不一致,可能导致上级与下级部门、部门与部门之间在海岸线数据的统计、利用甚至对外宣传方面出现不同的数据,进而在政府决策或是政策执行的过程中产生一系列问题和不利的影响等[12]。
鉴于海岸线长度的不确定性这一客观存在问题,为辽宁省海岸带资源的科学规划与可持续利用提供科学支撑,本文根据分形几何理论,在借鉴和总结前人研究成果的基础上,利用网格法和ArcGIS 10.2软件的空间分析工具,对辽宁省及其沿海丹东、大连、营口、盘锦、锦州和葫芦岛等6市海岸线的分维值、分形特征分别进行了计算与研究。
1 研究方法辽宁是我国海洋大省之一,地处我国海疆的最北端,横跨黄海、渤海,全省沿海行政区属自东向西包括丹东市、大连市、营口市、盘锦市、锦州市和葫芦岛市等6个地级市,大陆海岸线东起鸭绿江口,西止辽冀分界线,基岩港湾海岸与较平直的平原海岸交错分布。根据2008年辽宁省公布的数据,全省大陆岸线总长2 110 km,其中大连市1 371 km、葫芦岛市261 km、丹东市125 km、锦州市124 km、营口市122 km和盘锦市107 km[13]。
1.1 分形维数计算模型根据网格法和分形理论,当用不同的网格长度r量取海岸线时,会得到不同的网格数目N(r),则N(r)∝r-D,对其两边同时取自然对数可以得到lnN(r)=-Dlnr+C,其中,C为待定常数;D为被测海岸线的分形维数[6]。
通过Excel软件利用最小二乘法对不同的r值和N(r)值进行拟合并回归,直线斜率即为分形维数D,C是其纵截距。
1.2 测量尺度选取按照分形理论,各个量测尺度r的取值和取值间隔没有严格规定,但海岸线的分形属于随机前分形,是一种统计自相似,存在特定的标度区。为了更精确地求取分维值,网格法所用网格边长最小尺度rmin,可根据地图分辨率(0.5 mm地图单元)换算成实际距离而定。因此本文选取的最小量测尺度为25 m,rmin之后的尺度取值依次为rmin×2n(n=1,2,3,…),最大量测尺度根据lnr—lnN(r)坐标图上的直线段转折点判断、选取[9]。
2 应用及分析 2.1 全省海岸线的分形几何学特征以成图比例尺为1:5万的2017年辽宁省调查统计岸线为基础数据,利用ArcGIS 10.2软件的Features to Raster工具,设置不同的量测尺度r,分别得到相应的网格数量,即量测次数N(r),根据r、N(r)的双对数散点,建立辽宁全省及沿海6市海岸线的lnr—lnN(r)双对数图,同时进行最小二乘法拟合和线性回归分析,得到辽宁全省和沿海6市海岸线关于lnr和lnN(r)的拟合方程式及其拟合度优度参数(R2)和分形维数,辽宁全省及沿海6市海岸线的lnr—lnN(r)双对数坐标图如图 1所示,辽宁省及其沿海6市以及中国、世界其他国家或地区海岸线分维值如表 1所示。
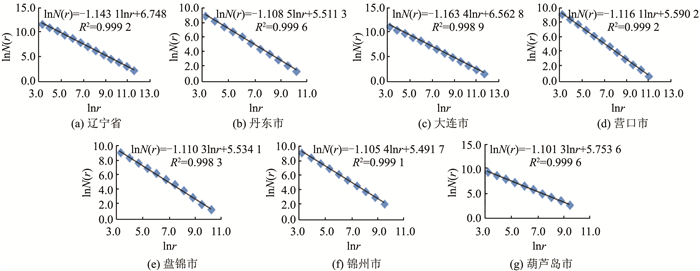 |
| 图 1 辽宁省及沿海6市2017年调查统计岸线量测尺度r与测量次数N(r)之间的双对数图 Fig.1 Double Logarithmic Map Between the Scale r of Coastline Measurements and the Number of Times of Survey in Liaoning Province and Six Coastal Cities in 2017 |
| 表 1 2017年辽宁省及沿海6市调查统计岸线及中国和世界不同区域海岸线分维值列表 Tab.1 List of Fractal Dimension Values of the Coastlines of Liaoning Province, Six Coastal Cities in Liaoning Province, China and Other Countries |
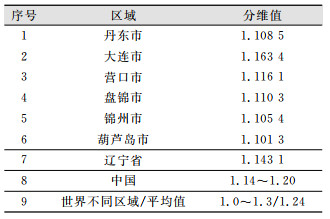 |
从图 1(a)可知,辽宁省2017年调查统计海岸线具有分形性质,分维值D为1.143 1。根据相关学者的计算,中国大陆海岸线虽然因分维方法的选取或岸线界定的标准不同,计算的分维值有差异,但总体相差不大,分维值介于1.14~1.20之间[9],而世界其他各地不同国家或区域海岸线的分维数大体在1.0~1.3之间,平均值大体为1.24[14]。从表 1可以看出,辽宁省海岸线的分维值不但低于中国大陆海岸线的分维值,且低于世界其他区域海岸线分维的平均值。从D值的定义来看,D值不仅表征了辽宁海岸线长度随测量尺度变化快慢程度;从几何意义上而言,还说明辽宁省海岸线的弯曲复杂程度低于全国和世界其他国家或地区海岸线平均水平。
另外,由图 1(b)~1(g)可以看出,辽宁沿海丹东市、大连市、营口市、盘锦市、锦州市和葫芦岛市海岸线同样具有分形性质,分维值分别为1.108 5、1.163 4、1.116 1、1.110 3、1.105 4和1.101 3。从表 1可以看出,大连市海岸线分维值最大,葫芦岛市海岸线的分维值最小,除大连市外,其他5市的海岸线的分维值都很接近,表明大连市海岸线的曲折复杂程度最高,其他5市海岸线弯曲复杂度相当。
2.2 全省海岸线的分形分维规律为了揭示辽宁全省、沿海6市海岸线分形空间分布规律,绘制了辽宁全省及沿海6市海岸线的分维值图,如图 2所示。从图 2可以看出, 辽宁省海岸线分维值D=1.143 1,介于沿海各市最大分维D大连市= 1.163 4和最小分维D葫芦岛市= 1.101 3之间,但并不等于沿海6市分维值的算术平均值D平均值=1.121 2,且算术平均值的分维大,趋向于局部最大的分维值D大连市=1.163 4,这一规律符合整体分维值趋向于局部分维值的最大值原则,遵循分形地貌学中的合并原理[15]。
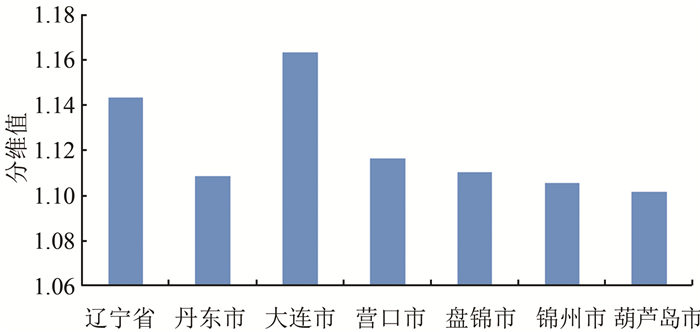 |
| 图 2 2017年辽宁全省及沿海6市海岸线的分维值图 Fig.2 Fractal Dimension Map of the Coastline of Liaoning Province and Six Coastal Cities in 2017 |
另外,按照区域地理位置,除丹东外,从东到西,海岸线分维值依次减少,反映了沿海各市海岸线曲折程度和分布情况。从辽宁沿海地质构造的沉降与隆起空间分布特征的视角来分析,大连市位于辽东半岛的南部,处于地质构造的地块抬升区,多为基岩海岸[16, 17],形成的岸线大多较为曲折,分形维数相对比较大,而葫芦岛市、锦州市、盘锦市、营口市位于辽河平原区,处于地质构造的沉降区[16, 17],形成的岸线较为平直,分形维数相对较小,这与上述计算结果相符。
2.3 沿岸活动对海岸线分形分维的影响近年来随着辽宁沿海经济带发展战略的不断推进,不同规模填海造地工程的实施,致使海岸线不断变化,为探究人类开发活动对辽宁省海岸线分形分维的影响,用上述方法计算了成图比例尺为1:5万的2008年辽宁省及沿海6市公布海岸线的分维值,计算结果如图 3,同时与2017年辽宁省及沿海6市调查统计岸线的分维值进行比较,如表 2所示。
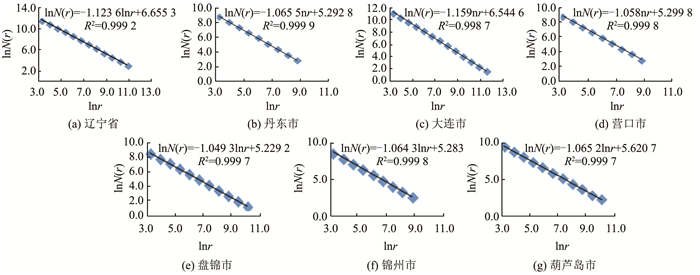 |
| 图 3 辽宁省及沿海6市2008年公布岸线量测尺度与测量次数之间的双对数图 Fig.3 Double Logarithmic Map Between the Scale of Coastline Measurements and the Number of Times of Survey Published in Liaoning Province and Six Coastal Cities in 2008 |
| 表 2 辽宁省及沿海6市海岸线2008年与2017年分维值及差值列表 Tab.2 Fractal Dimension and Difference Between 2008 and 2017 of the Coastline of Liaoning and Six Coastal Cities |
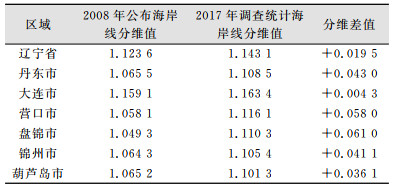 |
从表 2可以看出,辽宁全省及沿海各市海岸线的分维值都有所增加,表明海岸线的形状趋于复杂,其中盘锦市、营口市海岸线的分形维数变化最大,其次是丹东市、锦州市和葫芦岛市,大连市海岸线分形维数变化最小。
为满足沿海日益迫切的用地需求,在沿海地区,尤其是在辽东湾北部、西部的盘锦市、营口市、锦州市和葫芦岛市以及辽宁省东部丹东市这些易于开发的平原淤泥质和砂质海岸上,进行了港口码头、临港工业园区等围填海开发活动,这些开发规模大小不一、用海方式各异的用海活动改变了原来岸线的自然形态,一定程度上增加了海岸线曲折度,而多天然港湾的大连市,因建设过程中部分海岸被截弯取直,一定程度上减弱了海岸线弯曲度的增加。
3 结束语1) 2017年辽宁省调查海岸线具有分形性质,分维值D=1.143 1,表明辽宁省海岸线长度具有随测量尺度变化而变化的特征。因此,在制定全省海岸带保护规划、开发利用与管理等相关政策时,应考虑到辽宁省海岸线这一性质和特点,以实现海岸线资源的充分合理利用,另外建议在今后公布和使用海岸线长度数据时应附加说明岸线的分维值。
2) 辽宁沿海丹东、大连、营口、盘锦、锦州和葫芦岛等6市海岸线同样具有分形特征,分维值分别D丹东市=1.108 5、D大连市=1.163 4、D营口市= 1.116 1、D盘锦市= 1.110 3、D锦州市=1.105 4、D葫芦岛市=1.101 3,表明沿海各市海岸线在空间特征的分布上存在一定差异。
3) 辽宁省海岸线的分维遵循分形地貌学中的合并原理,即整体分维介于局部分维最大与最小值之间,且趋向于局部分维值的最大值。
4) 受沿海开发活动的影响,特别是港口码头和临港工业园区等人工填海造地使得辽宁全省和沿海6市海岸线的分维值有所增加,其中盘锦市、营口市海岸线的分形维数变化最大,其次是丹东市、锦州市和葫芦岛市,大连市海岸线分形维数变化最小。
| [1] |
Mandelbort B B. How Long is the Coast of Britain Statistical Self-Similarity and Fractional Dimension[J]. Science, 1967, 156(3775): 636-638. DOI:10.1126/science.156.3775.636 |
| [2] |
徐建华. 计量地理学[M]. 北京: 高等教育出版社, 2015.
|
| [3] |
朱晓华. 地理空间信息的分形与分维[M]. 北京: 测绘出版社, 2007.
|
| [4] |
Mandelbrot B B. Stochastic Models for the Earth's Relief, the Shape and the Fractal Dimension of the Coastlines, and the Number-Area Rule Forislands[J]. The National Academy of Sciences of the United States of America, 1975, 72(10): 3825-3828. DOI:10.1073/pnas.72.10.3825 |
| [5] |
Mandelbort B B. The Fractal Geometry of Nature[M]. San Francisco: W.H.Freeman and Company, 1982.
|
| [6] |
Liebovitch L, Toth T. A Fast Algorithm to Determine Fractal Dimensions by Box Counting[J]. Physics Letters A, 1989, 141(8/9): 386-390. |
| [7] |
Horne P, Suteanu C, Van Proosdij D, et al. Elevation-Pependent Multiscale Analysis of a Complex Intertidal Zone[J]. Journal of Coastal Research, 2013, 29(3): 631-641. |
| [8] |
Alexis M, Carlos A H, Maria G, et al. Fractal Analysis of the Complexity of Panama City Coastlines, Central America[J]. Revista Geografica, 2011, 149(1): 23-33. |
| [9] |
Su F Z, Gao Y, Zhou C H, et al. Scale Effects of the Continental Coastline of China[J]. Journal of Geographical Sciences, 2011, 21(6): 1101-1111. DOI:10.1007/s11442-011-0903-0 |
| [10] |
张云, 张建丽, 景昕蒂, 等. 1990年以来我国大陆海岸线变迁及分形维数研究[J]. 海洋环境科学, 2015, 34(3): 406-410. |
| [11] |
许宁, 高志强, 宁吉才. 基于分形维数的环渤海地区海岸线变迁及成因分析[J]. 海洋学研究, 2016, 34(1): 45-51. DOI:10.3969/j.issn.1001-909X.2016.01.006 |
| [12] |
朱晓华. 关于海岸线长度不确定性问题的研究[J]. 海洋开发与管理, 2000, 7(1): 23-25. |
| [13] |
辽宁省人民政府.辽宁省大陆海岸线[Z].沈阳, 2008
|
| [14] |
陈霞, 王建, 朱晓华. 用分形方法研究海岸线的长度[J]. 海洋科学, 2002, 26(12): 32-35. DOI:10.3969/j.issn.1000-3096.2002.12.009 |
| [15] |
艾南山, 李后强. 从曼德布罗特景观到分形地貌学[J]. 地理学与国土研究, 1993, 9(1): 13-17. |
| [16] |
全国海岸带和海涂资源综合调查成果编委会.中国海岸带和海涂资源综合调查报告[Z].北京, 1991
|
| [17] |
李从先, 范代读, 邓兵, 等. 构造运动与中国沿岸平原的地质灾害[J]. 自然灾害学报, 2002, 11(1): 28-33. DOI:10.3969/j.issn.1004-4574.2002.01.005 |
 2020, Vol. 45
2020, Vol. 45

