| 高原地区精密三角高程测量实践 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079
2. Key Laboratory of Precise Engineering & Industry Surveying, NASG, Wuhan 430079, China
几何水准测量[1]是传统的高程测量方法,它的理论研究、数据处理方面都趋于成熟,在工程、国家水准网中都得到了广泛的应用,它精度高,原理简单,但劳动强度较大,效率低。三角高程技术[1]的劳动强度较传统水准测量小,且在山区等地形起伏大的地区优势明显,效率高,但由于大气折光、仪器精度限制等原因,三角高程测量在高等级的水准测量中一直没有得到应用。
近年来,随着测量仪器和测绘技术的发展,由武汉大学学者提出的精密三角高程测量技术,创造性地解决了三角高程代替二等水准测量的难题[2-4]。该项技术在多地得到了应用,如高黎贡山[5]、舟山跨海高程测量[6, 7],并取得了极好的测量成果,但在高原地区还未得到应用。
相比之下,高原地区具有气压低、寒冷干燥、日照时间长、温差大、风力强劲的气候特点,以及高海拔的地形特点,因此水准测量具有大气折光变化大、大地水准面差距变化大等特点。本文以青海省藏区现代测绘基准体系基础设施建设兴海至同德二等水准测量项目为例,探讨在高原地区进行精密三角高程测量的作业方法及提高精度的措施。
1 精密三角高程测量原理 1.1 精密三角高程测量流程精密三角高程测量流程如图 1所示。
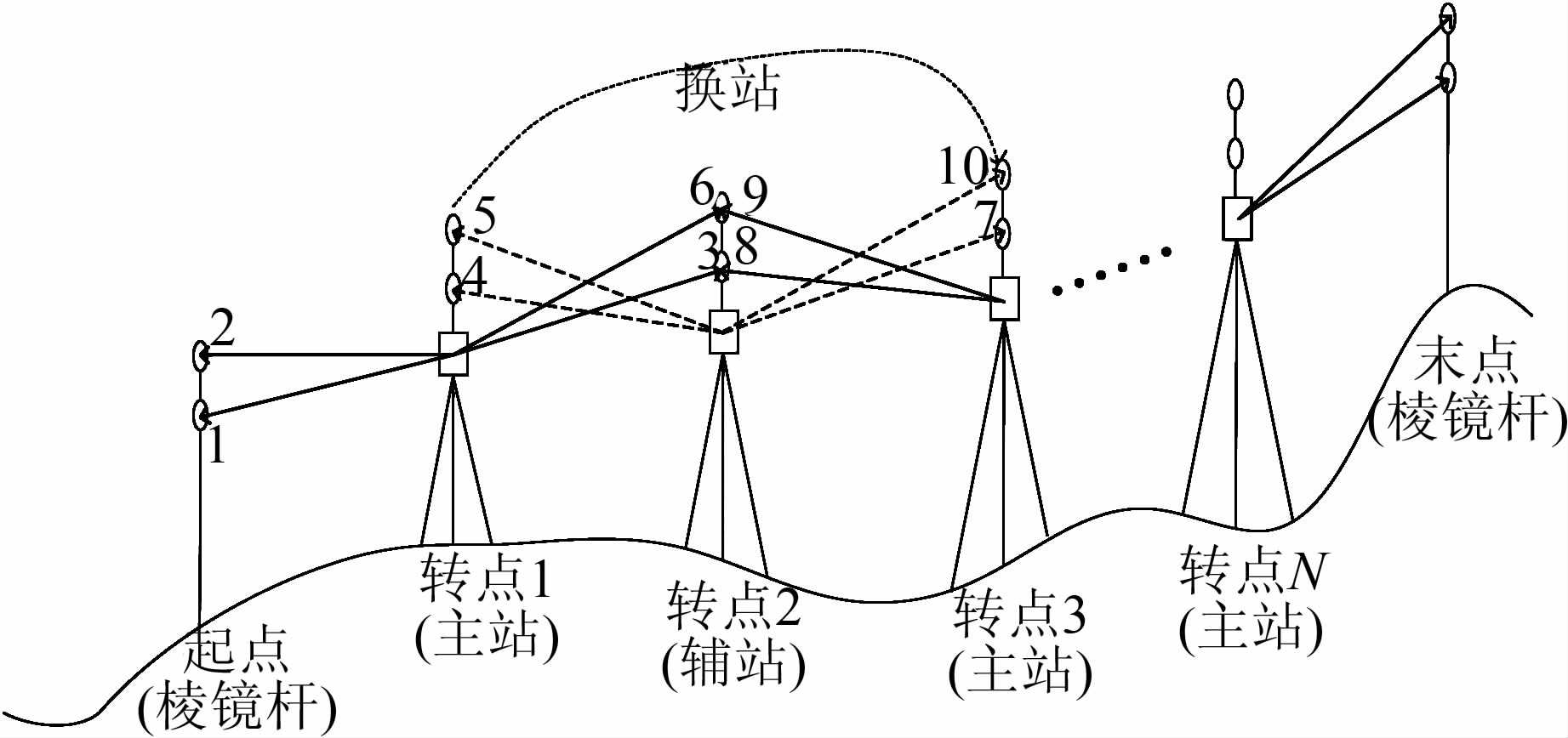 |
| 图 1 精密三角高程观测流程图 Figure 1 Flow Chart of Precise Trigonometric Leveling |
1) 测量之前,对所用仪器、脚架、棱镜杆进行检校;
2) 测量开始,在水准点上放置对中杆,在对中杆20 m以内架设主站(即观测对中杆的全站仪);
3) 依次对对中杆上高低棱镜进行观测;
4) 主站不动,在水准路线上布设辅站,按照后测站观测低棱镜、前测站观测低棱镜、前测站观测高棱镜、后测站观测高棱镜的顺序进行观测;
5) 辅站不动,主站换站,按照步骤4) 的顺序进行测量;
6) 如此往复,主站总是在奇数转点,辅站总是在偶数转点,将高程传递到下一个水准点;
7) 由主站对对中杆高低棱镜分别进行观测(对中杆高度应与该段水准路线起始点时的高度一致),完成测量。
1.2 精密三角高程测量观测方程经推导,精密三角高程测量的观测方程如下[2]:
| $\begin{align} & {{H}_{0n}}=[-{{D}_{1,0}}*cos{{Z}_{1,0}}+\frac{1}{2}\sum\limits_{2}^{n-1}{\left( {{D}_{i-1,i}}*cos{{Z}_{i-1,i}}-{{D}_{i,i-1}}*cos{{Z}_{i,i-1}} \right)} \\ & +{{D}_{n-1,n}}*cos{{Z}_{n-1,n}}\left] + \right[\sum\limits_{2}^{n-1}{\left( {{M}_{i-1,i}}+{{N}_{i-1,i}} \right)}] \\ & +\frac{{{S}_{1}}\left( {{\varepsilon }_{1}}-{{\varepsilon }_{m}} \right)-{{S}_{n}}\left( {{\varepsilon }_{n-1}}-{{\varepsilon }_{m}} \right)}{\rho \prime\prime }+\frac{\left( 1-{{K}_{n}} \right){{S}_{n}}^{2}-\left( 1-{{K}_{1}} \right){{S}_{1}}^{2}}{2R} \\ & +\frac{a{{e}^{2}}}{2}\left[ {{\left( {{B}_{0}}-{{B}_{1}} \right)}^{2}}co{{s}^{2}}{{B}_{0,1}}-{{\left( {{B}_{n}}-{{B}_{n-1}} \right)}^{2}}co{{s}^{2}}{{B}_{n-1,n}} \right] \\ \end{align}$ | (1) |
式中,右边第一项为概略高差,其中Di-1,i、Zi-1,i分别为架站点Pi-1观测架站点Pi低棱镜的斜距和天顶距;第二项为各转点垂线偏差及大气折光改正项(地球曲率已相互抵消),其中
高、低棱镜观测方程一样,测量时可相互检核,亦可作为往返测,大大减少了工作量。
1.3 精密三角高程测量误差分析由精密三角高程测量观测方程可以看出,精密三角高程测量的精度主要受仪器精度、垂线偏差、大气折光、地球曲率的影响。下面分析每一项的影响及其应对措施。
1) 仪器精度
影响因子为:
| $\begin{align} & -{{D}_{1,0}}\cdot cos{{Z}_{1,0}}+\frac{1}{2}\sum\limits_{2}^{n-1}{({{D}_{i-1,i}}\cdot cos{{Z}_{i-1,i}}-} \\ & {{D}_{i,i-1}}\cdot cos{{Z}_{i,i-1}})+{{D}_{n-1,n}}\cdot cos{{Z}_{n-1,n}} \\ \end{align}$ | (2) |
应对措施:使用高精度、具有自动照准的测量仪器,自动照准可以减少人为照准误差;测站上测量温度气压,并对距离进行改正,保证距离测量的准确性。
2) 垂线偏差
影响因子:在起末点表现为:
| $\frac{{{S}_{1}}\left( {{\varepsilon }_{1}}-{{\varepsilon }_{m}} \right)-{{S}_{n}}\left( {{\varepsilon }_{n-1}}-{{\varepsilon }_{m}} \right)}{\rho \prime\prime }$ |
在转点表现为:
| $\sum\limits_{2}^{n-1}{\frac{s}{2\rho \prime\prime }\left( {{\varepsilon }_{i-1}}-{{\varepsilon }_{i}} \right)}$ |
应对措施为:在高海拔以及高程起伏大的地区缩短观测边长。
3) 大气折光
影响因子:起末点表现为:
| $\frac{\left( 1-{{K}_{n}} \right){{S}_{n}}^{2}-\left( 1-{{K}_{1}} \right){{S}_{1}}^{2}}{2R}$ |
转点表现为:
| $\sum\limits_{2}^{n-1}{\frac{{{K}_{i,i-1}}-{{K}_{i-1,i}}}{4R}{{S}^{2}}}$ |
应对措施:起末点缩短观测边长,并让起末点的观测边长尽量接近;转点同时采用对向观测,注意避开不利时段。
4) 地球曲率
影响因子:起末点为:
| $\frac{a{{e}^{2}}}{2}\left[ {{\left( {{B}_{0}}-{{B}_{1}} \right)}^{2}}co{{s}^{2}}{{B}_{0,1}}-{{\left( {{B}_{n}}-{{B}_{n-1}} \right)}^{2}}co{{s}^{2}}{{B}_{n-1,n}} \right]$ |
转点的地球曲率被抵消。
应对措施:缩短起末点测站的观测边长。
2 青海省精密三角高程测量实践 2.1 测区概况本次精密三角高程测量项目为“青海省藏区现代测绘基准体系基础设施建设”项目的复测项目,测段为海南藏族自治州兴海县到同德县,该测段于精密三角高程测量前一个月进行了传统二等水准测量,可将两次测量的结果进行对照,以验证精密三角高程测量在高原地区的可行性。
测区海拔较高,兴海县位于青海省海南藏族自治州西南部,平均海拔3 924 m。同德县位于青海省东南部,平均海拔3 660 m。测段线路总长160余公里,包括一等水准点2个,即起末两点,二等水准点29个,均匀分布在测量线路中。测量线路所经区域大部分为滩地草原,高程起伏小;两处经过河流,高程起伏较大,达到500 m;整个测量线路中最大高差为1 039 m。高海拔以及高程起伏大对测量造成的影响是垂线偏差变化大,大地水准面差距大。
测区属于高原大陆性气候,具有气温低、昼夜温差大,降雨少而集中,日照长,太阳辐射强,高原季风强劲等特点,会对大气折光造成影响,进一步影响测量成果。
2.2 测量应对措施根据测区的测量条件及测量过程中遇到的各种问题,采取了以下措施进行应对。
1) 配备良好的软硬件
本次测量的硬件主要有4台全站仪,2套徕卡圆棱镜,1套徕卡对中杆。全站仪包括3台TM50,1台MS50,两台测量,两台备用。TM50的工作温度范围为-20 ℃~+50 ℃,防尘、防水、防雨,完全能够应对青海省多风、沙尘大、温差大且变化迅速的气候特点。仪器在每天使用之前应进行检定。
软件系统采用邹进贵教授课题组开发的精密三角高程系统[8]。该系统包括数据采集软件和数据处理软件两部分,其中数据采集软件运行在平板上,通过蓝牙和仪器连接,可以控制仪器进行自动化多测回观测,并对数据进行高低棱镜互差检核,保证数据质量。
2) 进行气象改正
全站仪电磁波测距是在地球的自然表面上、实际的大气条件下进行的,因此电磁波的传播速率会受到大气的影响,测得的距离需要经过改正才能得到两点间的倾斜距离。气象改正的实质是大气折射率对距离的改正,大气折射率n=c0/c,其中c0为光在真空中的传播速度,c为光在大气中的传播速度,因为折射率与温度、气压、湿度有关,所以通常称作气象改正[9]。
本次测量中,考虑到青海的气候条件,温度变化大、地形起伏大引起的气压变化大,携带了气压计、温度计、湿度计。每次架站之后,使用仪器测量出气压、温度、湿度三种气象要素,然后在全站仪上输入,仪器内部可自动进行距离改正。
3) 选择合适的测量时段
选择合适的测量时段主要是为了减弱大气折光[10, 11]的影响。太阳辐射强时,地面吸热,使得大气层离地面越近,温度越高;太阳辐射较弱,地面散热,地面温度逐渐低于上层大气,太阳辐射及温度的变化导致近地面的大气密度和折光差变化迅速且无规律,不宜进行观测。中午时分,太阳辐射强烈,空气对流剧烈,致使目标成像不稳定,通过全站仪可以观测到气浪,也不宜进行观测。加之测区地貌又以滩地草原为主,地面沙石多,比热容较小,因此温度随太阳辐射强弱变化十分迅速。太阳辐射强弱变化以及过强的太阳辐射对高原地区大气折光的影响较之其余地区尤为强烈。因此,为提高数据质量,应避开太阳辐射强弱变化大及太阳辐射过强的时段。
根据实践总结,每天的10:00~15:00是大气极不稳定的时间段,在该时间段观测,数据质量极差。掌握这个规律之后,测量时避开这个时段,选择大气稳定的时间段进行观测,可大大提高测量效率和数据质量。
4) 合理控制测量距离
控制测量距离,一方面可以减小大气折光的影响,另一个方面可以降低垂线偏差的影响[9]。
垂线偏差即地面上一点的重力向量g和相应椭球面上的法线向量n之间的夹角[9],总体来说,它的变化较平稳,但是在某些局部地区具有突变性质,且有很大幅度,这主要是由于地球内部质量密度分布的局部变化,如高山、海沟及其他不同地貌等因素引起的。为降低垂线偏差的影响,应在高海拔以及高程起伏大的地区缩短观测边长;然而,观测边长过短将降低测量效率,不能体现精密三角高程测量的优势。经实践发现,将观测边长控制在300~500 m,数据质量好,且测量效率高。
5) 进行水准面不平行性改正 由于地球内部物质分布并不均匀,地球的大地水准面是不平行的。而几何水准测量是依据水准面平行的原理测量高差的,因此即便水准测量没有误差,测得的某点高程也会和该点的正常高存在差异[9]。为解决这个问题,需要对水准测量测得的A、B两点的高差按照式(3) 进行正常位水准面不平行改正:
| $\varepsilon =-0.000\text{ }001\text{ }539\text{ }5\sin 2{{\varphi }_{m}}\cdot \Delta \varphi \prime {{H}_{m}}$ | (3) |
式中,φm是A、B两点的平均纬度;Δφ′=φA-φB是A、B两点的纬度差;Hm为两点间的平均高度(可用近似值代替)。
如在本次精密三角高程测量中,取两个水准点为例:Ⅱ兴巴1普纬度为35°45′26″,Ⅱ兴巴2普纬度为35°42′34″,由于高程数据保密,根据气压计测得了两点的概略高程Ⅱ兴巴1普为3 511 m,Ⅱ兴巴2普为3 451 m。根据式(3) 算得ε=14.54 mm,这个值对于二等水准测量来说非常可观。青藏高原地区纬度虽不高,但平均海拔达4 000 m,这导致水准面不平行改正非常大,因此在高原地区进行高程测量必须进行水准面不平行改正。
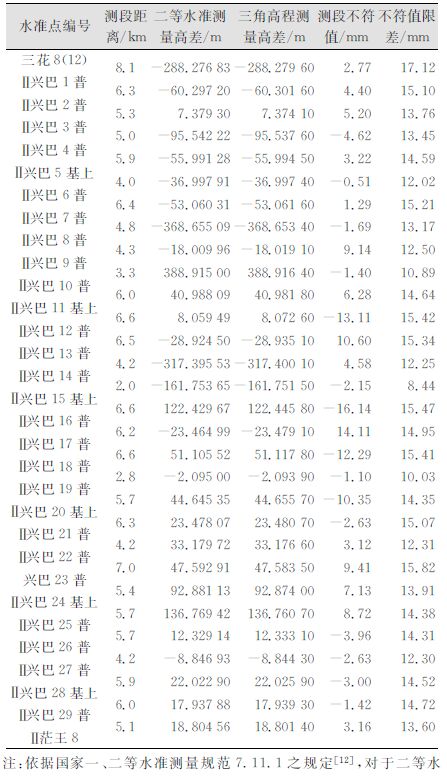
2.3 测量数据分析在完成数据采集工作之后,对数据进行了处理,数据处理结果如表 1所示。
| 表 1 精密三角高程数据处理结果 Table 1 Measurement Results of Precise Trigonometric Leveling |
 |
1) 不符值正态性分析
首先,对测段不符值进行正态性检验,以验证精密三角高程测量无系统性误差。由于各测段长度有异,应先将测段不符值归一化,即C=E/S,其中E为测段不符值(mm);S为测段长度(km);C为待检验值。
待检验值C的直方图和QQ图(分位数图)如图 2所示。
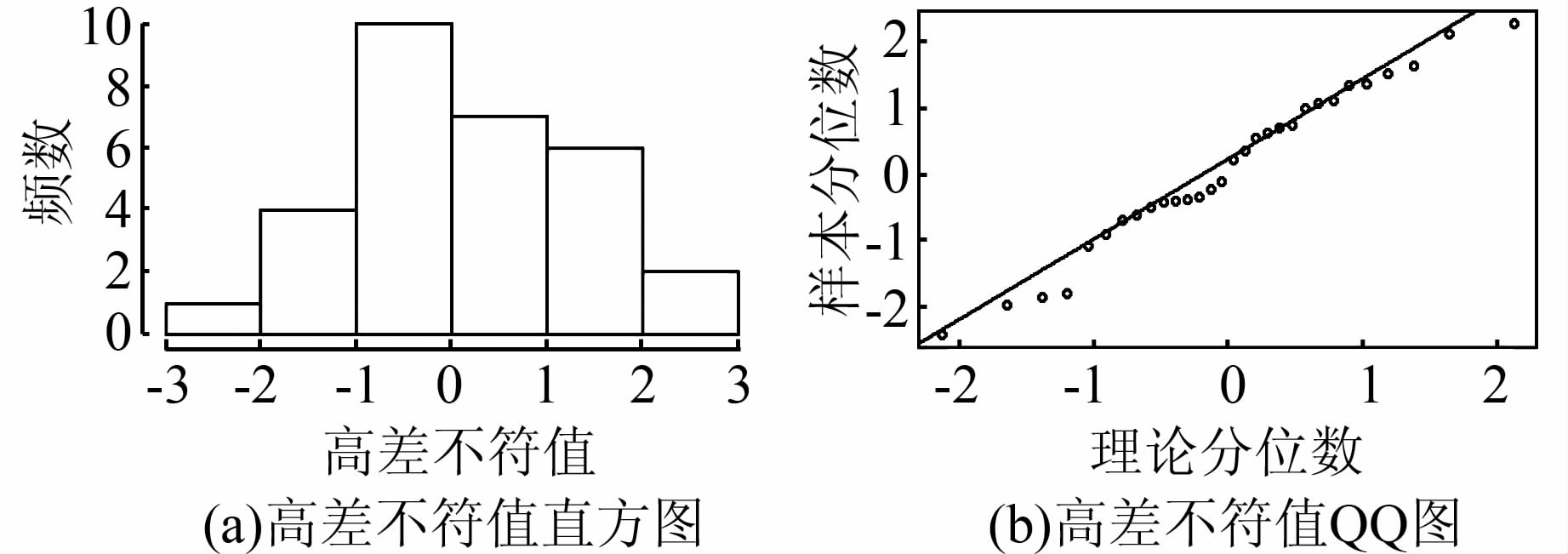 |
| 图 2 高差不符值的直方图和QQ图 Figure 2 Difference of Histogram and Normal QQ Plot Between Two Methods |
通过直方图 2(a)可以看出,待检验值C呈钟形分布,在0附近分布最多,往两边递减,有对称性;通过QQ图 2(b)可以看出,散点聚集在固定直线的周围。两者皆满足正态分布的图形表现。使用适用于小样本的Shapiro-Wilk检验得:W=0.975 3,接近1; p=0.691 6,显著大于0.05,符合正态分布,说明数据误差为随机误差,无系统误差,测量方法合理,数据可靠。
2) 不符值限差分析
通过对比测段不符值及其限差,发现测段不符值较大的几个测段集中在一起,即兴巴11基上到兴巴20基上,9个高差不符值有6个超过了10 mm,其中兴巴15基上到兴巴16普高差不符值超过限差0.67 mm。究其原因,这几个测段位于两县中间,对于只能住宿在县城内的测量人员来说,前往测点用时较长,为增加作业时间,在大气条件较差的时段进行了测量作业,从而降低了数据质量。这进一步说明选择合适的测量时段对提高数据质量的重要性。
除这几个测段,其余测段不符值都在±4 mm左右,精密三角高程测量结果和传统二等水准测量结果符合得非常好。
3 结束语本文首先介绍了精密三角高程测量的流程及观测方程,接着结合高原地区精密三角高程测量实践,分析了在高原地区进行精密三角高程测量需要采取的措施,最后对测得数据进行分析,得出了以下结论:
1) 在高原地区进行精密三角高程测量作业时,高原地区特有的气候条件及地理条件会对测量造成一系列的影响,表现在大气折光、垂线偏差以及水准面不平行性等方面。为减弱上述影响,应选择合适的测量时段,控制测量距离,并进行气象改正和水准面不平行性改正。
2) 通过和传统二等水准测量测得的数据比较,精密三角高程测量数据达到了较高的测量精度,满足国家二等水准测量的规范要求,证明了精密三角高程测量代替二等水准测量在高原地区的可行性。
| [1] |
潘正风, 程效军, 成枢, 等.
数字测图原理与方法[M]. 武汉: 武汉大学出版社, 2009 .
Pan Zhengfeng, Cheng Xiaojun, Cheng Shu, et al. Principles and Methods of Digital Mapping[M]. Wuhan: Wuhan University Press, 2009 . |
| [2] |
柏文锋, 熊斯, 黄利军, 等. 精密三角高程测量系统的研究与实现[J].
科技资讯,2010,(9) : 8–9.
Bai Wenfeng, Xiong Si, Huang Lijun, et al. The Study and Implement of Precise Trigonometric Leveling System[J]. Science & Technology Information,2010,(9) : 8–9. |
| [3] |
邹进贵, 徐亚明, 胡波, 等. 车载自动化精密三角高程测量系统研究[J].
测绘信息与工程,2010,35(4) : 30–32.
Zou Jingui, Xu Yaming, Hu Bo, et al. Automatic Precise Trigonometric Leveling System Based on Vehicle Platform[J]. Journal of Geomatics,2010,35(4) : 30–32. |
| [4] |
邹进贵, 徐亚明, 潘正风, 等. 基于TCRP1201全站仪的高程自动测量系统开发与应用研究[J].
测绘通报,2007,(12) : 30–33.
Zou Jingui, Xu Yaming, Pan Zhengfeng, et al. The Research on the Development and Application of Auto-height Surveying System Based on TCRP1201 Total Station[J]. Bulletin of Surveying and Mapping,2007,(12) : 30–33. |
| [5] |
邹进贵, 朱勇超, 童魁. 精密三角高程测量技术在高海拔山区的应用[J].
测绘地理信息,2013,38(6) : 6–9.
Zou Jingui, Zhu Yongchao, Tong Kui. Application of Precise Trigonometric Leveling Technology at High Altitude[J]. Journal of Geomatics,2013,38(6) : 6–9. |
| [6] |
赵尘衍, 袁庆华. 舟山群岛长距离跨海三角高程传递研究[J].
现代测绘,2015,(4) : 30–33.
Zhao Chenyan, Yuan Qinghua. Research on Long Distance Cross-Sea Height Transmission Based on Trigonometric Leveling in Zhoushan Islands[J]. Modern Surveying and Mapping,2015,(4) : 30–33. |
| [7] |
徐亚明, 施斌, 王代雄, 等. 改进的三角高程法在跨海高程传递中的应用[J].
测绘通报,2014,(4) : 65–67.
Xu Yaming, Shi Bin, Wang Daixiong, et al. An Improved Trigonometric Leveling Method for Cross-Sea Elevation Transfer[J]. Bulletin of Surveying and Mapping,2014,(4) : 65–67. |
| [8] |
邹进贵, 朱勇超, 胡波, 等. 测量机器人自动化垂直度与圆轴度检测系统研究[J].
测绘地理信息,2014,39(1) : 13–16.
Zou Jingui, Zhu Yongchao, Hu Bo, et al. Research on Automated Vertical and Round Detection System Based on Georobot[J]. Journal of Geomatics,2014,39(1) : 13–16. |
| [9] |
孔祥元, 郭际明, 刘宗泉.
大地测量学基础[M]. 武汉: 武汉大学出版社, 2010 .
Kong Xiangyuan, Guo Jiming, Liu Zongquan. Foundation of Geodesy[M]. Wuhan: Wuhan University Press, 2010 . |
| [10] |
王爱国. 大气折光和垂线偏差影响的三角高程测量的精度分析[J].
西部探矿工程,2007,(3) : 82–84.
Wang Aiguo. Accuracy Analysis of Trigonometric Leveling Allowing for the Effect of Atmospheric Refraction and Vertical Deflection[J]. West-China Exploration Engineering,2007,(3) : 82–84. |
| [11] |
蒋利龙, 施昆. 削减大气折光对三角高程影响的新途径[J].
测绘工程,2000,9(3) : 44–47.
Jiang Lilong, Shi Kun. New Method to Reduce the Effect of Atmospheric Refraction in EDM Trigonometric Leveling[J]. Engineering of Surveying and Mapping,2000,9(3) : 44–47. |
| [12] | GB/T 12897-2006.国家一、二等水准测量规范[S].北京: 中国标准出版社, 2006 GB/T 12897-2006.Specification for the First and Second Order Leveling[S].Beijing: China Standard Press,2006 |
 2016, Vol. 41
2016, Vol. 41

