| 无人机倾斜摄影云台倾角与三维模型详细度的关系探讨 |
倾斜摄影测量技术是新一代基于多角度观测的摄影测量技术[1],通过在同一飞行器上搭载多台传感器,同时从一个垂直、四个倾斜等5个不同的角度采集影像[2],打破了传统摄影只可以从一个垂直角度获取影像的局限性。结合后期快速建立三维模型技术,建立具有高精度的真三维模型[3],把人们带入一个符合人眼视觉的真实直观的世界[4]。
与传统航空摄影的大飞机相比,无人机以其方便、快捷、成本低廉的独特优势,得到了较为广泛的应用[5]。无人机倾斜摄影已经被越来越多的行业认可和应用,但其相对的国家技术标准一直没有明确,目前的作业方式大多处于“因人而异,各行其是”的阶段[6]。无人机倾斜摄影测量过程中,云台倾斜角度直接影响影像的质量,从而影响三维模型表达的详细程度。在拍摄之前,设置合适的云台倾角,使得尽可能全面地获取建筑物的侧面纹理,是本文研究的重点。
1 影响三维模型详细度的因素1) 遮挡因素。在倾斜摄影测量采集数据过程中,测区的高建筑物或者高地物都会影响相机拍摄光线,由于被遮挡的区域无法获取影像信息,无法提取特征点,从而不能进行匹配,导致后期建立的三维模型产生空缺,影响成果质量。
2) 云台倾角因素。云台倾角的大小对建筑物信息的侧面信息获取起着至关重要的作用。云台倾角过大,拍摄的庞大的数据量会使后期三维模型的建立变得非常缓慢,影响工作效率;云台倾角过小,会造成建筑物侧面的信息获取不完整[7-15],导致后期的建筑模型形成几何粘连。
无论是遮挡因素还是云台倾角因素,其本质都会影响建筑侧面信息的获取,拍摄区域遮挡物过多或者拍摄时云台倾角设置不合适都会造成后期三维模型的几何粘连。通过调整云台倾角,使得拍摄时遮挡面积达到最小,后期补拍的工作量也达到最少。
2 技术研究云台倾斜角度是指相机镜头偏离相机主光轴所形成的夹角。云台倾斜角度与建筑物的间隔、建筑物的高度以及无人机飞行高度之间的关系如图 1所示。
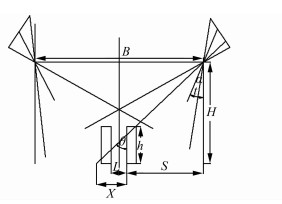 |
| 图 1 云台倾斜角与相关参数关系示意图 Fig.1 Schematic Diagram of Relationship Between Tilt Angle and Related Parameters |
由于两个设站之间的视线对称,因此在探讨云台倾角与拍摄详细度的关系时,考虑一边情况即可。图 1中,h代表建筑物高度(m);t代表云台倾斜角度;α代表相机的视角;L代表两建筑之间的间隔距离(m);H代表航高(m);S代表摄站垂直投影至平面的点到右侧建筑物边界的距离(m);X为建筑物投影至地面的阴影长度(m);θ角为刚好穿过建筑物顶端的光线与垂直方向的夹角;B为摄影基线长度(m)。
当X=L时,相机所能拍摄到的侧面纹理最全面,再结合图 1中所示的关系,可以得到:
| $ \begin{array}{c} \theta=\arctan \frac{L}{h} \end{array} $ | (1) |
| $ t-\alpha <\theta <t+\alpha $ | (2) |
| $ \arctan \frac{L}{h}-\alpha <t <\alpha+\arctan \frac{L}{h} $ | (3) |
为了保证拍摄影像的质量,侧视的视线要与下视的视线有一定的重叠角度,如图 2所示。
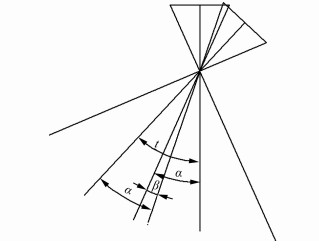 |
| 图 2 侧视与下视重叠范围示意图 Fig.2 Schematic Diagram of Overlapping Range of Side View and Down View |
则t的取值范围为:
| $ \alpha <t <2 \alpha-\beta $ | (4) |
对相机的视角进行讨论,如图 3所示。从图 3中可以得到如下数学关系:
| $ \tan \alpha=\frac{P}{2 f}=\frac{A u}{2 f} $ | (5) |
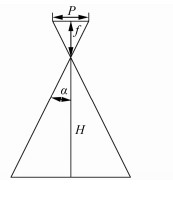 |
| 图 3 下视参数关系示意图 Fig.3 Schematic Diagram of Down View Parameter Relationship |
式中,A为相框长边上的像元个数;u为相机像元大小(μm);f为物镜镜头焦距(mm)。则有:
| $ \alpha=\arctan \frac{A u}{2 f} $ | (6) |
有的无人机已经提供了相机视角数值,因此在外业航拍时不需要根据式(6)再计算相机视角,直接代入α计算即可;对于没有提供相机视角数值的无人机,需要用式(6)进行计算。针对相机视角未知的公式推导如下:
再结合式(4)、式(5)即有以下推导公式:
1) 当
| $ \arctan \frac{L}{h}-\arctan \frac{A u}{2 f} <t <\arctan \frac{A u}{2 f}+\arctan \frac{L}{h} $ | (7) |
2) 当
| $ \arctan \frac{A u}{2 f} <t <\arctan \frac{A u}{2 f}+\arctan \frac{L}{h} $ | (8) |
3) 当
| $ \arctan \frac{L}{h}-\arctan \frac{A u}{2 f} <t <2 \arctan \frac{A u}{2 f}-\beta $ | (9) |
4) 当
| $ \arctan \frac{A u}{2 f} <t <2 \arctan \frac{A u}{2 f}-\beta $ | (10) |
在航摄之前,根据已知参数计算倾角并比较其大小,选择最小的角度范围作为云台倾斜的最佳角度范围。随着倾斜角度的增加,水平精度和高程精度均有提高,但高程精度提高更多。对于倾斜角为45°的倾斜影像,高程和平面定位精度相同。因此在云台倾斜角度的最佳范围确定后,要在考虑模型精度的前提下选择合理的云台倾斜角度。
3 实验分析以大疆单镜头精灵4Pro无人机为例,对某区域建筑物进行拍摄并构建三维模型。相关参数如下:建筑物平均高度h为30 m,建筑物平均间距L为19 m,相机焦距f为8.8 m,像元个数A为5 472(宽高比3:2),相机像元大小μ为241 μm,俯视与下视重叠度β为20°,航高H为80 m,飞行速度V为7.9 m/s,航向重叠度80%,旁向重叠度70%,飞行方式为“井”字型,拍照模式为等间距间隔拍照。将相关参数代入式(7)~式(10)中,计算出云台倾角的范围为37° < t < 54°。在考虑高程和平面精度的情况下,选择45°云台倾斜角度对测区进行拍摄,既满足了后期模型的详细度,又满足了精度要求。后期构建的三维模型如图 4所示。
 |
| 图 4 某地区建筑物模型 Fig.4 Building Model in an Area |
由图 4可以看出,采用合适的云台倾角拍摄的建筑物,后期构建的模型详细度比较高,几何粘连很少,避免了人工补拍,减少了工作量,提高了工作效率。
4 结束语本文通过研究建筑物高度、间距与云台倾角的关系,结合精度要求推导出了航拍不同高度和间距建筑物时的云台倾角的最适值,使得制作的模型详细度达到最高,减少了后期人工补拍的工作量,提高了工作效率。同时,因为云台倾角与模型详细度之间的关系涉及的因素过多,如果能够考虑到全部因素,本文的研究将更具有意义。
| [1] |
周晓敏, 孟晓林, 张雪萍, 等. 倾斜摄影测量的城市真三维模型构建方法[J]. 测绘科学, 2016, 41(9): 159-163. |
| [2] |
王伟, 黄雯雯, 镇姣. Pictometry倾斜摄影技术及其在3维城市建模中的应用[J]. 测绘与空间地理信息, 2011, 34(3): 181-183. |
| [3] |
Xiao J, Gerke M, Vosslman G. Building Extraction from Oblique Airborne Imagery Based on Robust Façade Detection[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 68: 56-68. DOI:10.1016/j.isprsjprs.2011.12.006 |
| [4] |
付博, 陈姗, 张俊. 无人机倾斜摄影测量技术在三维数字城市建模中的应用[J]. 湖南工业大学学报, 2019, 33(5): 79-83. |
| [5] |
孙杰, 林宗坚, 崔红霞. 无人机低空遥感监测系统[J]. 遥感信息, 2003(1): 49-50. |
| [6] |
曹正阳, 张明. 无人机倾斜摄影测量技术及其应用[J]. 科技经济导刊, 2019, 27(27): 45. |
| [7] |
刘辉, 张富文, 郑士举, 等. 无人机倾斜摄影测量技术在建筑测绘中的应用研究[J]. 建筑科技, 2018, 2(6): 64-67. |
| [8] |
廖永生, 陈文森. 无人机低空数字摄影测量参数计算和路线设计系统[J]. 测绘通报, 2011(9): 38-41. |
| [9] |
杨润书, 马燕燕, 殷海舟. 低空无人机航摄系统地面分辨率与航高的关系研究[J]. 地矿测绘, 2013, 29(3): 1-2. |
| [10] |
何敬, 李永树. 无人机航线规划参数分析研究[J]. 资源与人居环境, 2013(10): 26-28. |
| [11] |
仇春平, 卢晓攀, 王平论, 等. 无人机低空数字摄影测量成图精度实证研究[J]. 矿山测量, 2016(1): 67-70. |
| [12] |
张郁. 无人机低空摄影的精度分析与研究[J]. 测绘地理信息, 2018, 43(4): 59-61. |
| [13] |
柳静.无人机倾斜摄影测量三维模型绘制大比例尺地形图精度研究[D].西安: 西安科技大学, 2018
|
| [14] |
王京, 郭瑞隆, 马明义. 基于无人机倾斜摄影测量的三维重建及精度分析[J]. 测绘标准化, 2017, 33(3): 32-33. |
| [15] |
曹琳.基于无人机倾斜摄影测量技术的三维建模及其精度分析[D].西安: 西安科技大学, 2016
|
 2020, Vol. 45
2020, Vol. 45

