| GIS支持下的县乡公路网布局重要度解算方法 | [PDF全文] |
2. 长安大学公路学院,陕西 西安, 710064
2. School of Highway, Chang'an University, Xi'an 710064, China
中国县乡公路网在规模上占据运输系统较大比例,其布局的优劣影响着当地社会经济和运输业的发展。传统的公路网调整方法主要有交通区位线法和节点重要度法两种。交通区位线法是基于规划区域的经济和地理条件,结合干线交通道的主体走向构建路网的空间几何特征,对等级偏低的县乡公路网,交通区位线法作为一种远期的宏观布局方法在应用上受到一定局限;节点重要度法是将交通的发生区和吸引区抽象为节点,依据各个节点的经济、人口等指标信息以聚类的方法划分其重要程度进行路网布局[1],节点重要度法与经济发展层层递增辐射的理论相适应,但存在解算过程中重要节点的连接占比较大的问题,与节省资源和对经济发展的良性反馈机制贴合度不高。
本文将交通区位线-节点重要度联合的规划布局思想应用于宁波市县乡公路网布局调整中,应用GIS相关技术构建数字高程模型[2]模拟三维地形,结合当地主要节点的分布情况得到交通区位线,并分析路网重要度最大树可能存在的问题,优化最大树求解算法,通过GIS技术实现自动生成最大树,进一步实现线网的生成和显示,提高了与区域内实际县乡路网分布的拟合程度。
1 路网布局和交通区位分析1) 县乡等级路网布局调整思路。总结以往布局调整规划的经验,得出对于等级较低的县乡公路网规划的思路:①将规划区域的路网总体做区位分析,解算出区域内路网的走向主骨架,以此作为下一步调整工作的前提;②选择均势重要度法做路网布局优化工作,解算路网最优树作为县域县乡公路调整的基础和依据;③将交通区位线和路网最优树理论结合解算县乡路网的理论布局,利用所得的最优树对路网等级分布进行调整。
2) 结合数字高程模型的交通区位分析。交通区位线是依据所规划区域内部地理地势和经济结构所构建的交通高发虚拟线。用区域内高程数据构建50 m等高线,将县边界作为构建过程的硬断线,在ArcGIS中生成数字高程模型如图 1所示。拟合规划区域地形分布,明确区域内山脊线等地理特征位置走向[3]。
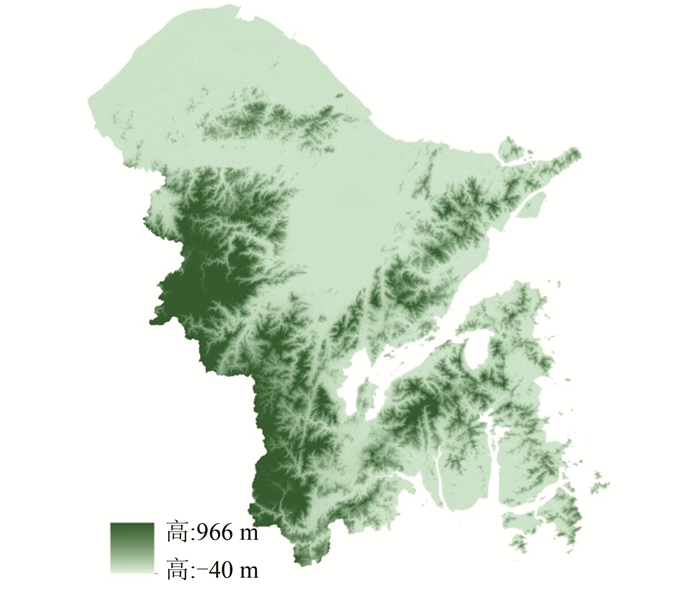 |
| 图 1 生成数字高程模型 Fig.1 Digital Elevation Model |
路网的主要功能是连通规划区域内部的运输通道和实现区域对外连接,即对内联络线、对外连接线两种:①对内联络线的载体是区域内部主要的经济运输要道,即各个主要节点之间的交通枢纽;②对外连接线的主要载体是国家干线网路及主要公路的连线[4]。
本文利用对规划区域的地理地貌、社会经济发展状况以及城市定位规划的统计分析,可得交通发生源有3 070个节点,以交通发生源作为控制点,连点成线,解算得到交通区位线,包括11条对外交通区位线(7横4纵)和11条区内交通区位线(6横4纵1环)。对外交通区位线如图 2所示; 区内交通区位线如图 3所示。
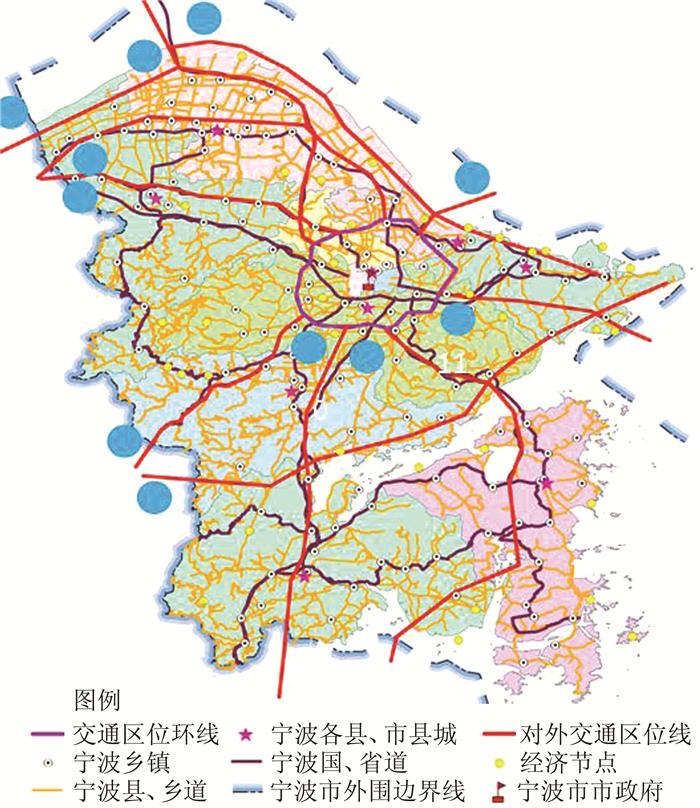 |
| 图 2 对外交通区位线 Fig.2 External Traffic Zone Line |
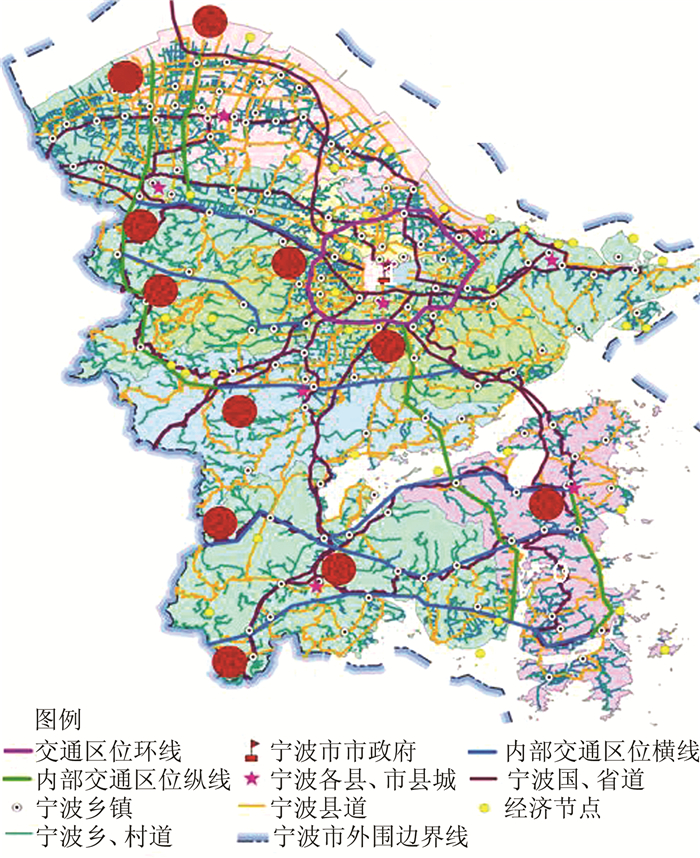 |
| 图 3 区内交通区位线 Fig.3 Internal Traffic Zone Line |
2 县乡路网均势重要度布局分析
均势重要度法旨在将把规划区域的各个子区域抽象理解为节点,将路网抽象为连接这些节点的连线[5]。可用主成分分析得到节点重要度权重,从而将节点按重要度划分层次。
以往所用的重要度布局法解算出的最大树存在与实际路网规划结果出入较大的问题,特别是在重要度稍低且节点较多的地区。原因是在解算最大树时未能重视路网布局形式,过多重视重要度最大的问题,导致重要度较低的节点与重要度较高的节点连接在一起,连接线舍近求远,布设不合理。
鉴于县乡路网布局规划中低等级节点过多的情况,尝试对节点重要度实施一定的修正后,利用图论算法解算最大树。相应的实施思路:首先,分层次进行布局,当完成第一层布局工作后,将所有节点的重要度动态更正成已连接节点的平均值;然后,进行下一等级节点的连接工作,从而解算重要度最大树。
所用到的均势重要度法涵盖选择节点、解算节点重要度及等级划分、解算路段重要度、生成最大树几个步骤。
2.1 选择节点、计算重要度和划分等级1) 确定节点和主要控制点。重要节点的选择原则基于当地的经济、地理、人文影响因素,主要节点包括:当地重要的工农业生产基地,对外交流门户(机场、火车站、码头等运输枢纽所在地),经济、政治、文化中心所在地,旅游景点,商业贸易交流中心,经济开发区等。
2) 计算节点重要度及划分等级。节点重要度是反映节点之间相对重要程度的一个变量,对于重要度的解算应当选择当地的社会经济、人口、GDP等数据作为指标信息对其进行量化的重要程度分析,选取权重归一化量化计算重要度[6]。
解算完成后按照所得到的节点重要度值进行排序,明确这些节点在规划区域的功能和地位。之后重新进行动态聚类分析,把上述的节点划分为6个层次,生成的节点重要度分布如图 4所示。
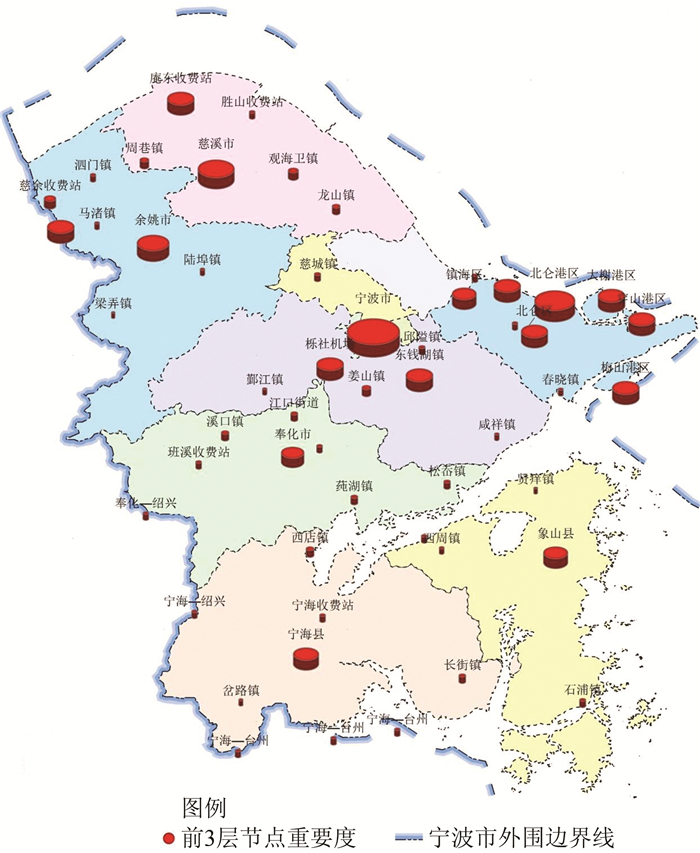 |
| 图 4 节点重要度 Fig.4 Area Node Importance |
2.2 路段重要度解算
对于求解、分层完成后的节点需对其进行节点连接,但鉴于路网之间地理、地势、政策、资金等的局限,不能逐一做到点点相连的完美情况,还需要分析节点之间怎样的连接可以实现县乡路网的最大效率。
路段重要度即所在路段的单位长度的重要度强度,用来表示路线各个边线的效率值。从而得到重要度最大树,即区域内的节点全部连通且内部不成圈而得到的路网形态[7]。确保解算得到的路网的重要度总和最大化,形成规划区域的路网主体架构。
2.3 基于ArcGIS的重要度最大树解算最大树解算方法主要有破圈法、避圈法、Prim算法。路网规划布局的一般思路为分层研究、逐层展开、整体优化[8]。此思路与Prim算法思路吻合,即节点分层,逐层解算。
使用GIS嵌入式开发平台ArcEngine进行所需功能的二次开发,编制出均势重要度最大树的Prim算法的解算程序。主要用到的均势重要度法的思路是在每层连接节点前,对上一层次的节点进行均势计算。在进行Prim解算时,必须对节点进行分层解算。为了计算效率和减少空间占用,对算法进行适当的优化处理。
存在图Gi=(Vi,Ei),以节点i的财政预算收入Gi作为第i层最大树的图,Vi囊括此层涉及到的节点,以Ei囊括涉及的边,另两集合的初始值设置为φ。另U={U1∩U2∩…∩Un},将Ui用以放置第i层节点,Ti用以放置第i层的最大树生成所得到的带权边。对节点进行分层次逐层解算最大树,数据冗余较少。依步骤解算最大树:①初始化过程:解算得到U1子集中所涉及的节点之间的带权边,存放于T1中;把集合U1的随意节点a存放在集合V1中,然后删除U1中的a。②首层节点实现最大树生成:在集合T1中比较起始点分别在集合U1和V1的带权边,选择重要度最大的边Eab,将其归进集合E1中,将节点b归入V1中,同时删除U1、T1中的节点b和边Eab,类推循环,直到U1=φ。③生成下一层最大树:在上一层节点重要度动态演变为此层所涉及的节点重要度的平均值时,在集合T2中生成U2及U2与V1间所有节点之间的带权边,在U2中选取任一节点依据步骤②对比解算,直至U2=φ。
此过程循环至所有层次结束。此时已连接所涉及全部节点,且做到每层Gi中存放该层解算所得到的最大树,帯权边集合Ti为里程等级,提供了数据备选。自动解算求出的最大树如图 5所示。对比路网里程规模预测值对其进行路网加密,可对每层添加边数以对应每一图层,便于布局规划的对比分析。
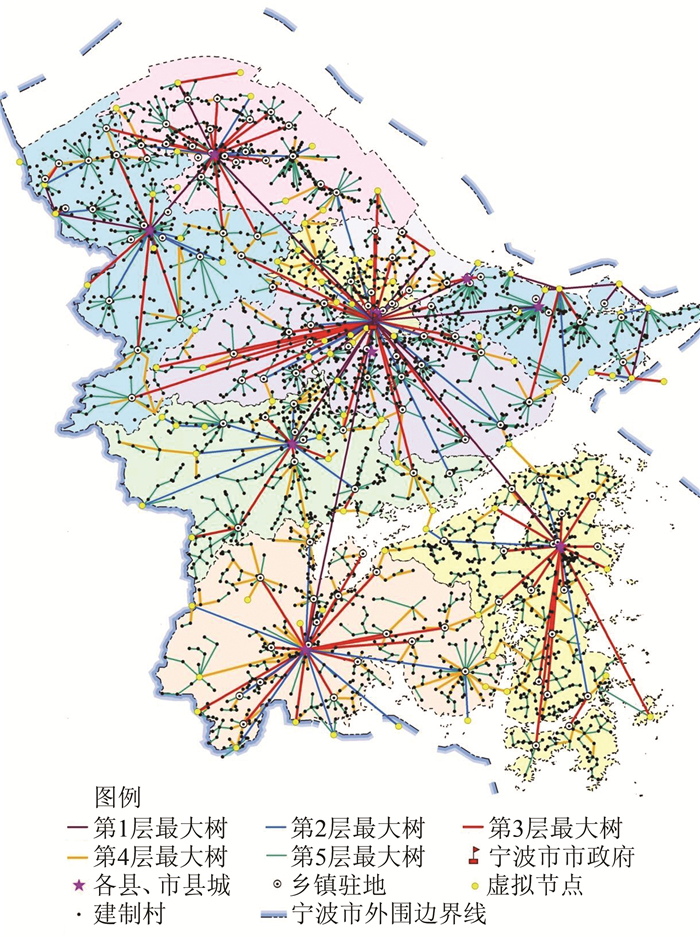 |
| 图 5 节点重要度最大树 Fig.5 Importance of the Maximal Tree |
3 理论路网布局生成
交通区位线和节点重要度最大树构成主骨架布局,由主骨架布局和节点层次划分形成理论布局方案,如图 6所示。
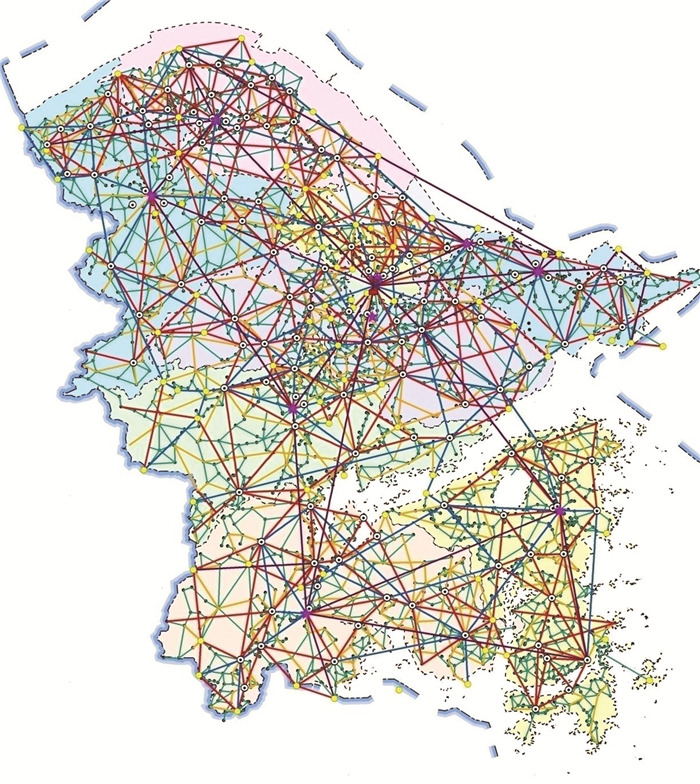 |
| 图 6 公路网理论布局 Fig.6 Road Network Theory Layout |
方案中,第1层路网将各县市中心区与市中心、对外出口以及重要的交通经济节点连接起来,等级对应国道;第2层路网使所有县市之间能快速通达,等级对应省道;第3层路网使各乡镇之间连通度高,等级对应县道;第4层路网连接当地主要的建制村、中心村与邻近的乡镇,等级对应乡道;第5层路网连接邻近的建制村,等级对应村道。
调整后的县乡公路网规模更趋合理,多项指标达到更高水平,带动社会发展的能力更强,对外连通性更加优越,内部交通节点的通达率有所提高。
4 结束语GIS技术可在区位线方法的基础上,采用交通区位与数字高程模型结合的方法,利用相关工具对节点的重要度进行量化显示以解算主要区位线和重要度最大树。现阶段的区位线解算主要依据当地的地理和经济信息进行绘制,对未来规划区域的地理形态进行三维模拟,可以具体显示区域山脊线等地理特征;再将主要经济节点、主要道路桥梁等信息量化显示在三维地图上,通过研究实现区位线的自动化求解和显示。
| [1] |
胡列格, 程立勤. 基于节点重要度交通区位布局法的城市群公路网布局研究[J]. 铁道科学与工程学报, 2008(1): 87-90. DOI:10.3969/j.issn.1672-7029.2008.01.018 |
| [2] |
李志林, 朱庆. 数字高程模型[M]. 武汉: 武汉大学出版社, 1998.
|
| [3] |
余红举, 吴晨曜, 周军元, 等. 多源数据生产DEM方法探索[J]. 测绘地理信息, 2016, 41(6): 86-88. |
| [4] |
邵春福. 交通规划原理[M]. 北京: 中国铁道出版社, 2004.
|
| [5] |
王元庆, 崔世华, 郝素斌. 重要度区位联合农村公路网布局法[J]. 中国公路学报, 2002(4): 89-92. |
| [6] |
段智, 袁振洲. 基于Prim算法的农村公路网布局重要度最大树求解方法[J]. 公路, 2007(5): 111-114. |
| [7] |
丁斌. 动态Fuzzy图最大树聚类分析[J]. 数值计算与计算机应用, 1992(2): 157-160. |
| [8] |
张树升, 周伟. 公路网规划的总量控制法[J]. 华东公路, 1996(2): 42-46. |
 2019, Vol. 44
2019, Vol. 44

