| 基于小波去噪的非等间距多点灰色预测模型 |
2. 广西空间信息与测绘重点实验室,广西 桂林,541000
2. Guangxi Key Laboratory of Spatial Information and Geomatics, Guilin 541000, China
变形预测的方法主要有回归分析法、时间序列分析法、BP神经网络法等。这些方法通常要求有大量样本,而且要求具有典型的概率分布,这在实际生产中难以实现,限制了其使用范围[1]。灰色预测模型针对小样本数据处理具有一定的优越性,传统的灰色预测模型主要有灰色GM(1, 1)模型、非等间距灰色GM(1, 1)模型、多变量灰色GM(1,n)等,这些灰色预测模型大多是单点或者等间距的。而在实际的建筑工程中,由于各方面因素的影响,变形观测所获得的数据可能是不等间距的。除此之外,建筑物的变形状态都布设有大量的变形监测点,监测点间是相互影响、彼此关联的[2]。单点的灰色模型没有利用监测点间的相互关系信息,等间距灰色模型没有考虑非等间距带来的误差。所以对多个变形监测点的非等间距观测数据建立非等间距多点灰色模型进行变形关联预测具有重要意义。但是,在对变形体的监测过程中,不可避免要受到外界环境的影响,或由于自身的系统性偏差,使得观测值包含了真实信号和误差两部分[3]。为了客观地对变形进行分析和解释,从观测数据中分离出噪声并提取变形特征,分析监测点的变形规律是十分必要。小波具有较好的时频特性,在沉降位移和噪声的区分、有效去除噪声保留有用信息方面较其他方法有明显的优势[4-5]。本文针对常规非等间距多点灰色模型在这方面存在的不足,将该模型与小波去噪相结合,利用小波原理对实际变形观测值进行去噪处理,然后再建立非等间距多点灰色预测模型进行变形分析与预测。
1 非等间距多点灰色预测模型 1.1 小波去噪原理非线性小波变换阈值去噪方法(nonlinear wavelet threshold value)主要是针对信号中混有白噪声的情况,根据白噪声在小波变换域的能量主要集中于幅值较低的小波系数特点,而白噪声在任何正交基上的变换仍然是白噪声,并且有着相同的幅度,信号的小波系数必然大于那些能量分散且幅值较小的噪声小波系数,这样可设计一阈值,使低于该阈值的小波系数变为零,从而使信号中的噪声得到有效抑制[6-7]。该方法得到是原始信号的近似最优估计,具有较广泛的适用性。
设对叠加了高斯白噪声的有限长度信号,某一尺度j时小波变换系数为yj=Ajf(x)可表示为:
| $ {y_j} = {x_j} + \delta {z_j} $ | (1) |
式中,xj为原始信号的小波变换系数;δ为常数且δ>0,是噪声级;zj为一个标准的高斯白噪声, 服从正态分布N(0, σ2)。
本文采用软阈值函数去噪的方法,在最大程度地去除小波大幅值系数中噪声的情况下,尽可能完整地保留有用信号的小波系数,使去噪后的信号与原始含噪信号之间的误差尽可能地减小,从而达到去噪的目的[8-9]。
1.2 非等间距多点灰色预测模型的建立设T=(T1, T2, T3, …, Tn)为某基坑沉降监测的一组时间序列,Tk-Tk-1≠const(固定值),并且k=2, 3, …, n,X(0)(T)表示各个基坑沉降监测点在各观测时间段内的实际沉降观测量矩阵:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}\left( T \right) = \left\{ {{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}\left( {{T_1}} \right),{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}\left( {{T_2}} \right),{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}\left( {{T_3}} \right), \cdots ,} \right.}\\ {\left. {{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}\left( {{T_i}} \right), \cdots ,{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}\left( {{T_n}} \right)} \right\}} \end{array} $ | (2) |
式中,X(0)(Ti)表示各基坑沉降监测点在观测时段Ti的沉降观测值向量,即X(0)(Ti)=(X1, Ti(0), X2, Ti(0), X3, Ti(0), …, Xm, Ti(0))T,m为基坑沉降点监测点数目,序列(Xi, T1(0), Xi, T2(0), Xi, T3(0), …, Xi, Tn(0))为非等间距序列,时间间距ΔT=Ti-Ti-1。
为了发掘数据中隐藏的规律,对基坑实际沉降观测量矩阵进行一次累加生成,得到一次累加生成矩阵X(1)(T):
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}\left( T \right) = \left\{ {{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}\left( {{T_1}} \right),{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}\left( {{T_2}} \right),{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}\left( {{T_3}} \right), \cdots ,} \right.}\\ {\left. {{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}\left( {{T_i}} \right), \cdots ,{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}\left( {{T_n}} \right)} \right\}} \end{array} $ | (3) |
式中,
| $ \begin{array}{l} \frac{{{\rm{d}}x_1^{\left( 1 \right)}}}{{{\rm{d}}t}} = {a_{11}}X_1^{\left( 1 \right)} + \cdots + {a_{1n}}X_n^{\left( 1 \right)} + {b_1}\\ \;\;\; \vdots \\ \frac{{{\rm{d}}x_m^{\left( 1 \right)}}}{{{\rm{d}}t}} = {a_{m1}}X_1^{\left( 1 \right)} + \cdots + {a_{mn}}X_n^{\left( 1 \right)} + {b_m} \end{array} $ | (4) |
记
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}}}{{{\rm{d}}t}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{X}}^{\left( 1 \right)}} + \mathit{\boldsymbol{B}} $ | (5) |
设Lj(Ti+1)是Xj(1)(t)在[Ti Ti+1]区间上的背景值,Lj(Ti+1)取Xj(1)(t)的近邻均值,则有:
| $ {\mathit{\boldsymbol{L}}_j}\left( {{T_{i + 1}}} \right) = \frac{1}{2}\left( {\mathit{\boldsymbol{X}}_j^{\left( 1 \right)}\left( {{T_i}} \right) + \mathit{\boldsymbol{X}}_j^{\left( 1 \right)}\left( {{T_{i + 1}}} \right)} \right) $ | (6) |
将微分方程(5)离散化,确定辨识参数A,B的最小二乘估计,设ai=(ai1, ai2, …, ain, bi),ai的最小二乘估计为:
| $ {{\hat a}_i} = {\left( {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right)^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ | (7) |
式中,
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{L_1}\left( {{T_2}} \right)}& \cdots &{{L_m}\left( {{T_2}} \right)}&1\\ {{L_1}\left( {{T_3}} \right)}&{}&{{L_m}\left( {{T_3}} \right)}&1\\ \vdots &{}&{}& \vdots \\ {{L_1}\left( {{T_n}} \right)}& \cdots &{{L_m}\left( {{T_n}} \right)}&1 \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{Y = }}{\left( {\mathit{\boldsymbol{X}}_{i,{T_2}}^{\left( 0 \right)},\mathit{\boldsymbol{X}}_{i,{T_3}}^{\left( 0 \right)}, \cdots ,\mathit{\boldsymbol{X}}_{i,{T_n}}^{\left( 0 \right)}} \right)^{\rm{T}}}。$ |
令
| $ {{\mathit{\boldsymbol{\hat X}}}^{\left( 1 \right)}}\left( {{T_i}} \right) = {{\rm{e}}^{\mathit{\boldsymbol{\hat A}}\left( {{T_i} - {T_1}} \right)}}{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}\left( {{T_1}} \right) + {{\mathit{\boldsymbol{\hat A}}}^{ - 1}}\left( {{e^{\mathit{\boldsymbol{\hat A}}\left( {{T_i} - {T_1}} \right)}} - I} \right)\mathit{\boldsymbol{\hat B}} $ | (8) |
还原后Ti时段的灰色预测值(即非等间距多点预测模型)为:
| $ {{\mathit{\boldsymbol{\hat X}}}^{\left( 0 \right)}}\left( {{T_i}} \right) = \frac{{\left( {{{\rm{e}}^{\mathit{\boldsymbol{\hat A}}\left( {{T_i} - {T_1}} \right)}} - {{\rm{e}}^{\mathit{\boldsymbol{\hat A}}\left( {{T_{i - 1}} - {T_1}} \right)}}} \right){\mathit{\boldsymbol{X}}^{\left( 0 \right)}}\left( {{T_1}} \right) + {{\mathit{\boldsymbol{\hat A}}}^{ - 1}}\left( {\left( {{{\rm{e}}^{\mathit{\boldsymbol{\hat A}}\left( {{T_i} - {T_1}} \right)}} - {{\rm{e}}^{\mathit{\boldsymbol{\hat A}}\left( {{T_{i - 1}} - {T_1}} \right)}}} \right)\mathit{\boldsymbol{\hat B}}} \right)}}{{\Delta {T_i}}},i = 1,2,3, \cdots ,n $ | (9) |
一般通过计算模型的拟合精度和模型预测的平均相对误差来检验非等间距多点预测模型预测结果的可靠性[10-11]。
1) 模型的拟合精度计算公式为:
| $ {\sigma ^2} = \frac{1}{{nm}}\sum\limits_{i = 1}^m {\mathit{\boldsymbol{V}}_i^{\rm{T}}{\mathit{\boldsymbol{V}}_i}} $ | (10) |
式中,
2) 记ρtk模型tk时刻预测值的平均相对误差,其计算公式为:
| $ \rho = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{\left| {{\mathit{\boldsymbol{V}}_i}\left( {{T_k}} \right)} \right|}}{{\left| {\mathit{\boldsymbol{X}}_{i,{T_k}}^{\left( 0 \right)}} \right|}}} \times 100\% $ | (11) |
本文实验数据来源于文献[2],选取位于某基坑北侧边坡上相互关联的3个沉降监测点A、B、C的监测数据进行整体变形分析与建模。实验选取3个沉降监测点前11期数据进行建模,然后分别用基于小波去噪的非等间距多点灰色预测模型和非等间距多点灰色预测模型对后两期的沉降量进行预测。
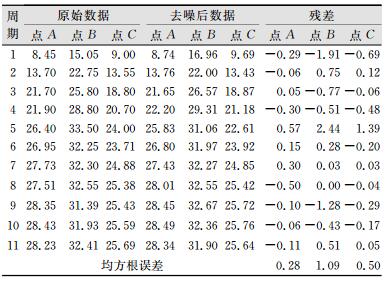
2.1 小波去噪处理本文方法首先利用软阈值函数的sym4小波对A、B、C 3个点前11期变形观测数据进行两层分解与重构,即去噪处理;然后运用去噪处理后的数据建立非等间距多点灰色预测模型。去噪前后的数据对比表及去噪效果图见表 1、图 1。
| 表 1 去噪前后数据对比/mm Tab.1 Comparison of Datas Before and After Denoising/mm |
 |
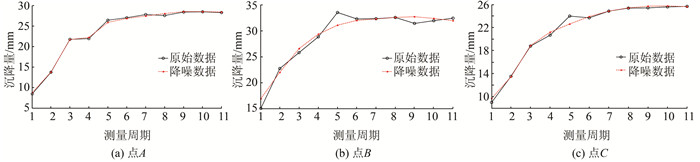 |
| 图 1 去噪效果 Fig.1 Result of De-noising Effect |
通过去噪前后数据对比表可知,除了点B的去噪信号均方根误差稍微有点大外,点A、C的去噪信号均方根都较小,所以整体滤波效果较好。由去噪效果图可以看出,原始观测数据在个别测量周期出现了较大数值的异常波动,经小波去噪处理后,变形信号曲线变得比较光滑,所以经小波去噪后的观测值可有效地削弱随机误差的干扰和去除噪声,使数据更接近基坑变形的真实情况,对非等间距多点灰色预测模型的建立有较大的帮助。
2.2 模型预测1) 模型参数计算。通过表 1去噪后的数据建模计算基于小波去噪的非等间距多点灰色预测模型参数:
| $ {{\mathit{\boldsymbol{\hat A}}}_1} = \left[ {\begin{array}{*{20}{c}} { - 0.135}&{0.083}&{0.044}\\ { - 0.128}&{0.072}&{0.048}\\ { - 0.086}&{0.067}&{0.009} \end{array}} \right];\;\;\;{{\mathit{\boldsymbol{\hat B}}}_1} = \left[ {\begin{array}{*{20}{c}} {10.759}\\ {18.708}\\ {10.992} \end{array}} \right] $ |
通过原始观测数据建模计算非等间距多点灰色预测模型参数:
| $ {{\mathit{\boldsymbol{\hat A}}}_2} = \left[ {\begin{array}{*{20}{c}} { - 0.219}&{0.071}&{0.151}\\ { - 0.300}&{0.062}&{0.251}\\ { - 0.179}&{0.057}&{0.124} \end{array}} \right];\;\;\;{{\mathit{\boldsymbol{\hat B}}}_2} = \left[ {\begin{array}{*{20}{c}} {10.562}\\ {17.753}\\ {10.678} \end{array}} \right] $ |
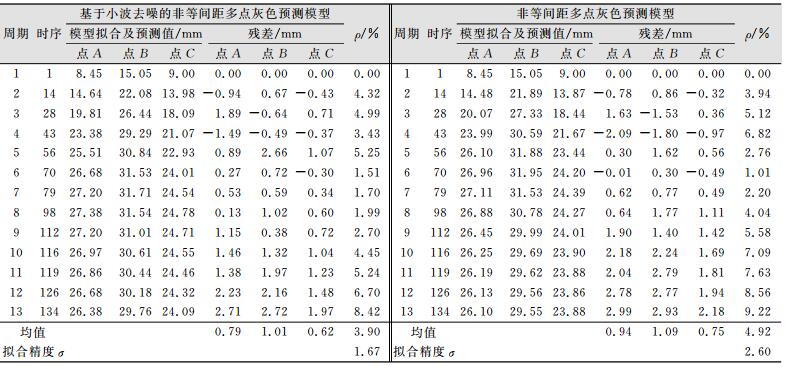
2) 拟合值和预测值计算。由式(9)~式(11)计算得到基于小波去噪的非等间距多点灰色预测模型和非等间距多点灰色预测模型的拟合值及预测值、模型的拟合精度及预测值的平均相对误差见表 2。
| 表 2 基于小波去噪的非等间距多点与非等间距多点灰色预测模型拟合与预测结果 Tab.2 Fitting and Forecasting Results of non-Equidistant Multi-point Gray Model Based on Wavelet Denoising and non-Equidistant Multi-pointgray Model |
 |
2.3 预测结果对比与分析
根据表 2,绘制两种模型拟合值及预测值对比图如图 2所示,并得到两种模型预测结果的对比表如表 3所示。表 3中,ρ表示各个变形监测点预测值平均相对误差的均值。
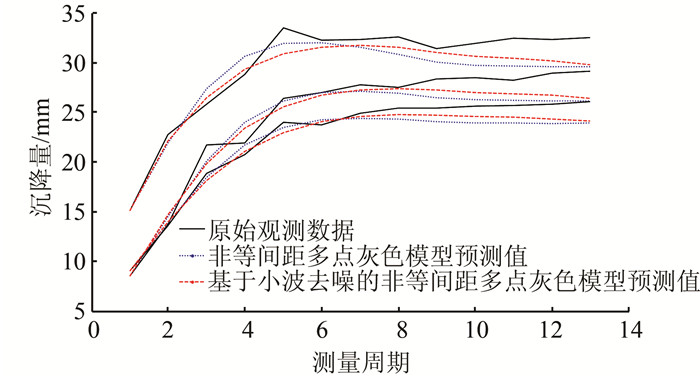 |
| 图 2 两个模型拟合值及预测值对比 Fig.2 Comparison of Fitting Values and Predictive Values for Two Model |
| 表 3 两种模型预测结果对比 Tab.3 Comparison of the Forecast Results for Two Model |
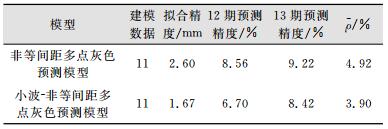 |
分析表 2~表 3可知,非等间距多点灰色预测模型得到A、B、C 3个监测点的第12期预测值平均相对误差为8.56%,第13期预测值平均相对误差为9.22%,模型拟合精度为2.60;而基于小波去噪的非等间距多点灰色预测模型得到A、B、C 3个监测点的第12期预测值平均相对误差为6.70%,第13期预测值平均相对误差为8.42%,模型拟合精度为1.67。除此之外,后者的残差均值和预测值平均相对误差均值都小于前者。通过对比以上两个模型可以得出,基于小波去噪的非等间距多点灰色预测模型的预测精度和拟合精度,都优于非等间距多点灰色预测模型。
通过对图 2中两个模型拟合值及预测值曲线的对比,也可以看出基于小波去噪的非等间距多点灰色预测模型较非等间距多点灰色预测模型,预测曲线更接近于原始观测数据曲线,而且拟合效果更好。说明原始观测数据经小波去噪后,再建立模型进行预测,是有效可行的。
3 结束语1) 小波阈值去噪方法有硬阈值法和软阈值法。硬阈值法去噪会将不属于噪音的有用信息去掉,所以本文采用的软阈值法去噪更具工程实用性。
2) 基于小波去噪的非等间距多点灰色预测模型解决了原模型无法实现对非平稳、含噪时间序列信号进行优化处理的问题,使原模型的拟合精度和预测精度得到了提高,是一种优于非等间距多点灰色预测模型的有效预测方法,适合在变形预测中应用。
不过,本文用于小波去噪处理的数据量少,而且小波基是靠经验和多次实验对比选取的,这对后期建立的非等间距多点灰色预测模型的预测精度有很大影响,在以后的研究工作中有待改正。
| [1] |
康超, 黄声享, 李洋洋. 小波去噪和新陈代谢GM(1, 1)相结合应用于变形预报[J]. 测绘地理信息, 2015, 40(6): 46-48. |
| [2] |
尹晖, 周晓庆, 张晓鸣. 非等间距多点变形预测模型及其应用[J]. 测绘学报, 2016, 45(10): 1140-1147. DOI:10.11947/j.AGCS.2016.20160005 |
| [3] |
黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 2版. 武汉: 武汉大学出版社, 2010.
|
| [4] |
刘闯, 花向红, 赵杰, 等. 基于小波去噪的高铁沉降预测模型研究[J]. 测绘地理信息, 2015, 40(1): 38-40. |
| [5] |
王建波, 栾元重, 许君一, 等. 小波分析桥梁变形监测数据处理[J]. 测绘科学, 2012, 37(3): 79-81. |
| [6] |
李超, 郝建新, 文鸿雁, 等. 变形监测数据的一种小波去噪法研究[J]. 测绘科学, 2012, 37(4): 65-66. |
| [7] |
高成, 董长虹, 郭磊, 等. MATLAB小波分析与应用[M]. 2版. 北京: 国防工业出版社, 2007.
|
| [8] |
向东, 贡建兵. 变形序列小波消噪最佳分解尺度量化指标的确定[J]. 武汉大学学报·信息科学版, 2014, 39(4): 467-470. |
| [9] |
尹晖, 朱锋. 时序数据去噪中的小波策略及评价指标[J]. 武汉大学学报·信息科学版, 2012, 37(11): 1374-1377. |
| [10] |
Wang Qijie, Wang Changcheng, Xie Rong'an, et al. An Improved SCGM(1, m) Model for Multi-point Deformation Analysis[J]. Geosciences Journal, 2014, 18(4): 477-484. DOI:10.1007/s12303-014-0012-z |
| [11] |
尹晖, 陈永奇, 张琰. 贫信息条件下的多点变形预测模型及其应用[J]. 测绘学报, 1997, 26(4): 365-372. |
 2018, Vol. 43
2018, Vol. 43

