| 融合BP神经网络的组合模型地铁结构变形预测 |
城市发展,交通先行。随着城市中心区域的高密度开发和人群高密度集中,交通出行总量剧增,交通拥堵现状日益严重,地铁交通无疑成为缓解地面交通压力、实现人车立体分流、解决交通拥堵的最佳公共交通方式之一。截至2020年12月31日,中国内地共计44座城市开通城市轨道交通,运营里程达7 715.31 km。地铁建设已成为一种必然的趋势,根据预测,到21世纪末,世界上将有近三分之一的人口要乘坐地铁去工作和生活[1]。随着越来越多的轨道交通线路建成运营,提高运营质量,保障运营安全的需求将日益突出,中国的城市轨道交通同时蕴藏着巨大发展机遇与挑战。
运行速度快、运营系统化、发车间隔短、运载人口密度高是地铁运营的4大主要特征,由此决定了地铁运营对安全的高标准,以杜绝地铁运营事故的发生。监测数据不仅描述监测对象的实际变形状态,更蕴含了变形发展趋势的预兆信息。事故发生往往不是纯偶然事件的,都有一个时间过程,通过分析监测数据中蕴含的预兆信息,为地铁安全运营提供可靠的数据支持,将事故遏制在萌芽之中。随着测量机器人、自动化监测系统、多传感器集成系统等高新技术的不断应用,变形监测积累的资料繁多,数据信息量庞大,研究如何及时、有效地从大量变形监测信息中挖掘有效数据信息,进行变形分析、解释,并对变形作短期和中、长期预测等具有重要的理论意义和实用价值[2]。目前变形预测数学模型主要有时间序列分析模型、回归分析模型、灰色理论模型、神经网络模型、卡尔曼滤波等[3, 4]。但由于系统或模型的不确定性,试图通过越来越复杂的单一模型预测接近真实常常会导致模型精度的虚假乐观[5-7]。
不同类型的变形预测模型具有各自的适用性及精度等级。1969年,Bates和Granger首次提出了组合预测理论[8],并证明2种或2种以上无偏的单项预测模型可以按某种规则进行组合,获得的组合预测结果优于任何单一预测模型,为预测领域提供了新的研究思路。
1 BP神经网络优化一般而言,所建数学模型与客观实际之间往往是有差异的,这种差异称为模型误差[9]。经过众多学者对模型误差的研究,现已形成了系统误差理论、粗差理论、统计诊断理论、方差-协方差估计理论和抗差估计理论等[9-11]。通过对模型误差进行理论优化后,将获得更高的预测精度,但将该理论应用于组合模型的预测结果优化效果如何,还鲜有研究。本文采用BP(black propagation)神经网络优化组合模型,提高组合的模型预测精度。
1.1 BP神经网络算法原理自20世纪50年代以来,人们相继提出了各种各样的学习算法,其中Romelhart和Mcclelland提出了误差反向传播算法(error back propagation algorithm,简称BP算法)。它采用最速下降法的学习规则,通过误差反向传播来不断优化网络的阈值和权值,使得最终的网络误差平方和最小。标准的BP神经网络拓扑结构一般包含输入层、隐含层和输出层3部分,其中隐含层允许存在多个。同层神经元之间互不连接,每一层的神经元只接受前一层神经元的输出。其输入层神经元通常采用线性传递函数,隐含层和输出层神经元则可根据具体问题选择Sigmoid型传递函数或线性传递函数,如图 1所示。
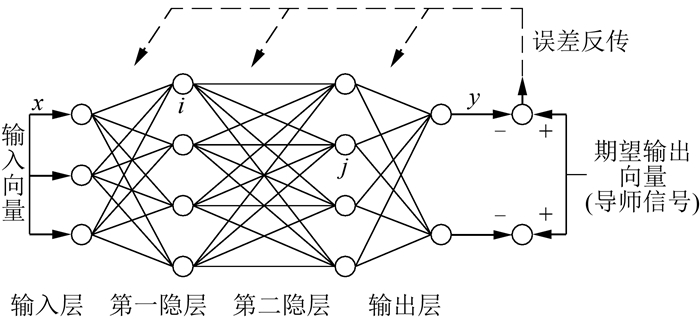 |
| 图 1 神经网络结构图 Fig.1 Neural Network Structure |
1.2 BP神经网络优化组合模型
模型是人为构造出来的用于模拟真实值的方式,不可避免的会与真实值之间存在误差,即模型误差。若真实值为y=z(x)而人为构造的模型为y'=f(x),则Δf=y-y'即为模型误差。如果能采用某种方法获得Δf,就可对y'进行模型误差的补偿,人为构造的模型就得到优化,得到的预测值z(x)=f(x)+Δf将更接近于真模型,从而可以使得预测精度得到进一步提高。这种优化组合模型的BP神经网络结构层为(n+1)×p×1,如图 2所示。
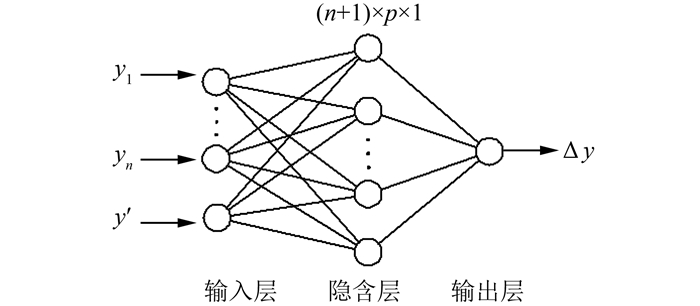 |
| 图 2 BP-时间序列网络结构图 Fig.2 BP-Time Series Network Structure |
从图 2所示的BP神经网络结构图中,输入层层数为n+1,输入数据为y1、y2、…、yn、y',y'表示组合模型的预测值,n为用于模型组合的单一模型个数; 这种模型优化的实质是:组合模型预测值y'作为BP神经网络的输入层之一,输出层Δy即表示真值与BP神经网络计算值之间的偏差值。其目的是通过学习样本的拟合来预测预测样本的估计值,通过求出Δy的BP神经网络估计值ΔyBP,便可对组合模型进行优化,优化公式为:
| $ \bar y = y' + \Delta {y_{{\rm{BP}}}} $ | (1) |
最终,y即为组合模型优化后的预测值。
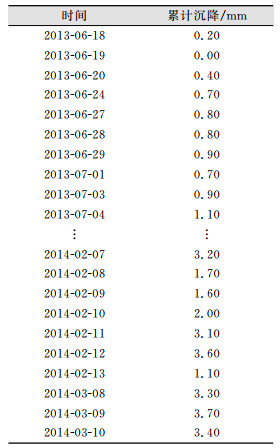
2 工程应用将文中所述方法应用于南京某地铁线自动化监测数据,以分析该方法的适用性及精度。通过构建时间序列模型和回归分析模型,并基于误差平方和最小准则构建回归-时间序列预测模型,并创新性的通过BP神经网络对回归-时间序列预测模型的预测结果进行模型优化,进一步提高模型预测精度。原始数据为监测点Z方向的变形值,得到Z方向累计变形值,如表 1所示(由于篇幅有限,只列举了一部分数据),共有266期沉降数据,前207期数据定为训练样本,后59组数据为预测样本。累计变形曲线如图 3所示。
| 表 1 监测点Z方向累计变形值 Tab.1 Accumulated Deformation in Z Direction |
 |
 |
| 图 3 Z方向累计沉降曲线图 Fig.3 Accumulated Deformation in Z Direction |
2.1 构建时间序列模型
样本数据中的时间间隔不一致,故采用三次样条插值法对缺失的时间序列进行插值,得到连续的等时间间隔的Z方向坐标,再求得连续的等时间间隔的Z方向累计沉降。通过EVIEW软件计算得到时间序列模型MA(2)为:
| $ \begin{array}{l} x\left( t \right) = 0.007\;073 - 0.504\;16a\left( {t - 1} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;0.304\;716a\left( {t - 2} \right) \end{array} $ | (2) |
列车运行的振动、临近施工的扰动等都是影响既有地铁结构变形的主要因素,这些因素都与时间有着直接的联系。因此,构建本文案例的回归分析模型其本质即为建立变形量与自变量之间的函数关系。从Z方向累计沉降曲线图显示,地铁结构变形随时间具有周期性变形规律,且根据土体沉降规律及累计沉降曲线可得出,Z方向变形随时间的变化率逐渐减小。故在构建回归分析模型中,可加入周期变化。本文拟采用的多元回归模型有:
| $ {y_t} = {a_0} + {a_1}t + {a_2}\ln t $ | (3) |
| $ {y_t} = {a_0} + {a_1}\ln t + {a_3}{t^2} $ | (4) |
| $ {y_t} = {a_0} + {a_1}\sqrt t + {a_2}\sin \left( {wt} \right) + {a_3}\cos \left( {wt} \right) $ | (5) |
| $ {y_t} = {a_0} + {a_1}\ln t + {a_3}\sin \left( {wt} \right) + {a_4}\cos \left( {wt} \right) $ | (6) |
| $ {y_t} = {a_0} + {a_1}\sqrt t + {a_2}{t^2} + {a_3}\sin \left( {wt} \right) + {a_4}\cos \left( {wt} \right) $ | (7) |
式中,yt为时刻t的期望值(变形值); t为某时刻到首次观测日期的累计时间(d);
根据上面所构建的5种多元回归模型分别称为A、B、C、D、E模型,将Z方向累计沉降数据进行预处理后输入SPSS软件中,求得多元回归方程的系数分别为:
| $ A:{y_t} = - 1.252 + 1.07\ln t - 0.007t $ | (8) |
| $ B:{y_t} = - 1.176 + 0.979\ln t $ | (9) |
| $ \begin{array}{l} C:{y_t} = 1.104 + 0.164\sqrt t - 0.131\sin \left( t \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.006\cos \left( {wt} \right) \end{array} $ | (10) |
| $ \begin{array}{l} D:{y_t} = 0.206 - 0.113\ln t + 0.022\sin \left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.66\cos \left( {wt} \right) \end{array} $ | (11) |
| $ \begin{array}{l} E:{y_t} = - 1.021 - 0.155\sqrt t + 1.187\ln t - \\ \;\;\;\;\;\;\;\;\;0.094\sin \left( t \right) + 0.05\cos \left( {wt} \right) \end{array} $ | (12) |
将式(8)~式(12)的回归模型分别对预测样本数据进行地铁结构变形预测,计算得到模型预测结果中误差如表 2所示。
| 表 2 各个模型预测中误差/mm Tab.2 Prediction Accuracy of Each Prediction Models/mm |
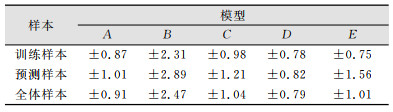 |
由表 2可知,模型D在预测精度明显好优于其他模型,故最终的回归分析模型采用模型D,即式(11):yt=0.206-0.113lnt+0.022sin(t)+0.66cos(wt)。
2.3 组合模型权重解算获得误差最小的预测结果是本应用的主要目标,故本文采用基于误差平方和最小准则构建组合模型,解算组合模型权系数,基于误差平方和最小准则[12]表达式为:
| $ \begin{array}{l} \mathit{\boldsymbol{W}} = {\left( {{w_1}\;\;\;{w_2}} \right)^{\rm{T}}}, \mathit{\boldsymbol{R}} = {\left( {1\;\;\;1} \right)^{\rm{T}}}, \mathit{\boldsymbol{E}} = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}_1^{\rm{T}}{\mathit{\boldsymbol{e}}_1}}&{\mathit{\boldsymbol{e}}_1^{\rm{T}}{\mathit{\boldsymbol{e}}_2}}\\ {\mathit{\boldsymbol{e}}_2^{\rm{T}}{\mathit{\boldsymbol{e}}_1}}&{\mathit{\boldsymbol{e}}_2^{\rm{T}}{\mathit{\boldsymbol{e}}_2}} \end{array}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ {\begin{array}{*{20}{c}} {\min {J_1} = {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{EW}}, }\\ {{\rm{s}}.{\rm{t}}.\;\;{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{W}} = 1} \end{array}} \right. \end{array} $ | (13) |
式中,w1表示组合模型中时间序列模型的权重; w2表示组合模型中回归分析模型的权重; ei=(ei1, ei2, …, eiN)T(i=1, 2),表示第i种单项预测方法的预测误差列向量。解得权重值为:
| $ {w_1} = 0.175, {w_2} = 0.825 $ |
本工程实例构建的的BP神经网络优化模型结构和主要参数如表 3所示。
| 表 3 BP神经网络模型结构及参数 Tab.3 Structure and Parameters of BP Neural Network Model |
 |
通过以上BP神经网络结构得到的补偿值ΔyBP,优化后的组合模型预测精度与各个模型的精度比较如表 4所示。
| 表 4 各个预测模型地铁结构变形预测结果精度比较/mm Tab.4 Prediction Accuracy of Each Prediction Model/mm |
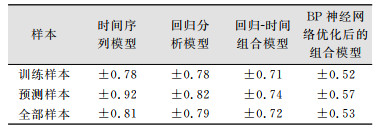 |
由表 4可知,本文所采用的回归-时间序列组合预测模型在预测阶段,比时间序列模型的预测结果提升19.57%,比回归分析模型的预测结果提升9.76%以上。经过BP神经网络优化后的组合模型预测较优化前精度提升22.97%,比时间序列模型的预测结果提升了27.17%,比回归分析模型的预测结果提升38.04%。由此可知,本文所采用的组合模型比单一模型的预测精度都得到提升,而通过BP神经网络优化后的组合模型预测精度得到进一步提升。
3 结束语监测精度更高、实时性更好、可靠性更强是未来变形监测发展的重要趋势,也是预防工程事故发生的重要保障。本文研究构建基于BP神经网络优化的组合模型,并应用于既有运营地铁结构变形值的预测,研究结果表明该方法应用于预测运营地铁结构变形方面具有较高的适用性和精度,为地铁结构变形预测提供科学而有效的技术方法。
| [1] |
郑怀德. 试论广州市地下空间开发利用管理体制改革[J]. 地下空间与工程学报, 2013, 9(1): 8-12. |
| [2] |
文鸿雁. 基于小波理论的变形分析模型研究[D]. 武汉: 武汉大学, 2004
|
| [3] |
叶俊华. 基于自适应卡尔曼滤波的灰色模型改进及在变形预测中的应用研究[D]. 西安: 长安大学, 2012
|
| [4] |
岳春芳, 宋金元. RBF神经网络组合模型在GPS高程拟合中的应用[J]. 测绘地理信息, 2020, 45(1): 20-22. |
| [5] |
Chatfield C. Model Uncertainty and Forecasting Accuracy[J]. Journal of Forecasting, 1996, 15(7): 495-508. DOI:10.1002/(SICI)1099-131X(199612)15:7<495::AID-FOR640>3.0.CO;2-O |
| [6] |
赵宇, 谢谟文文, 杜伟超. 城市轨道交通地面沉降雷达遥感监测分析[J]. 测绘地理信息, 2017, 42(5): 66-69. |
| [7] |
梅文胜, 于安斌, 王忠仁. 新型地铁轨道控制网复测精度控制指标分析[J]. 测绘地理信息, 2017, 42(2): 114-117. |
| [8] |
Bates J M, Granger C W J. Combination of Forecasts[J]. Operations Research Quarterly, 1969, 20(4): 451-468. DOI:10.1057/jors.1969.103 |
| [9] |
陶本藻. 测量数据处理的统计理论和方法[M]. 第2版. 北京: 测绘出版社, 2014.
|
| [10] |
杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1994.
|
| [11] |
孙海燕. p-范分布理论及其在测量数据处理中的应用[D]. 武汉: 武汉大学, 1995
|
| [12] |
王建平. 组合预测权重计算公式的探讨[J]. 预测, 1993, 12(4): 54-55. |
 2021, Vol. 46
2021, Vol. 46

