| 光谱余弦修正在多光谱传感器辐射校正中的研究 | [PDF全文] |
2. 武汉大学遥感农作物表型实验室,湖北 武汉,430079;
3. 中国资源卫星应用中心,北京,100094
2. Laboratory for Remote Sensing and Crop Phenotyping, Wuhan University, Wuhan 430079, China;
3. China Centre for Resources Satellite Data and Application, Beijing 100094, China
随着遥感技术的不断发展,遥感产品的需求也由定性走向定量[1, 2]。辐射校正成为遥感数据处理的重要构成部分,也是遥感产品定量化应用的基础和前提[3-6]。
目前,除了前期的实验室定标和星上定标,在轨定标也很重要,这一阶段的定标通常利用标准定标场作为地表参照,以场地定标和交叉定标最为常见[7, 8]。场地定标主要是以经验线性回归模型为基础,建立传感器入瞳处辐射量与传感器输出数字值之间的关系[9]。Naughton等[10]利用美国的Rail Road Valley Playa定标场和Ivanpah Playa定标场,对德国RapidEye卫星的多光谱影像数据进行了辐射定标;黄妙芬等[11]利用场地定标获取了北京一号小卫星多光谱相机辐射定标系数;勾志阳等[12]利用高光谱辐射特性靶标,采用反射率基法对无人机多光谱影像进行了辐射定标。经验线性回归方法是以单通道为核心,利用多余观测值,使用最小二乘方法计算的[13],但是地物光谱谱段间的联系是客观存在的[14],此种方法忽视了谱段间的联系,不仅不能充分利用光谱信息,而且使校正精度受到影响。在辐射校正过程中,波段间的影响不是单一的线性关系,所以光谱信息在校正过程中不容忽略。
本文充分考虑谱段间的关系,提出了一种光谱余弦修正的辐射校正方法。为了利用谱段间的联系,拟针对无人机遥感影像数据辐射校正问题,对地面、航空数据进行处理,在场地定标的基础上,突破光谱余弦修正的关键技术,通过研发相关算法实现遥感影像数据的辐射校正处理,求解出更优的辐射校正模型。为了验证改进方法的适用性,本文拟分析改进前后光谱反射率的变化情况,并与实测光谱进行对比。
1 实验过程 1.1 数据观测本次实验于2019-09-18开展,实验区域位于湖北省武汉市江湾体育公园一带,实验同步采集了地面和无人机数据。
1) 地物光谱测量。本文中的地面光谱数据由美国ASD FieldSpec Pro便携式地物波谱仪采集获得,简称ASD数据,测量地物包含植被、马路和水体等多种类型,地物类型丰富,地物面积较大且均匀。在研究区域铺设标准定标毯6块,均匀选取50个地面目标。每个样本采用5点取样法,每点进行5次光谱测量,25条光谱曲线中剔除异常值,其余的平均值被用作地面目标的参考光谱。在这50个样本中,抽取20个样本用于辐射校正算法研究,而剩余30个样本用作验证数据。
2) 机载多光谱影像。使用Tetracam公司由12个微型相机组成的Mini-MCA相机获取影像,中心波长(单位:nm)分别为490、520、550、570、670、680、700、720、800、850、900、950,影像量化级为8 bit。大疆8旋翼无人机通过200 m飞行高度获取空间分辨率分别为0.1 m的影像。
1.2 兼顾光谱信息的辐射定标研究本实验中,兼顾光谱信息的辐射定标方法主要有以下几个步骤:
1) 无人机各波段定标参数计算。
在本研究中,无人机飞行高度是在200 m的低空进行的,在低空飞行状态下,成像光谱数据具有的特点是传感器和地面之间的大气影响相对较小,利于以线性关系建立地面反射率与数字值之间的关系[15]。每个像素的反射率可以利用式(1)进行计算:
| $ \rho_{i}=G_{i} D_{i}+B_{i}(1 \leqslant i \leqslant 12) $ | (1) |
式中,ρi和Di分别是在波段i中定标毯的反射率值以及对应无人机影像中的数字值;Gi和Bi为传感器在波段i时的增益和偏置。在影像中选择定标毯对应的像元,所选像元的反射率是定标毯的反射率。利用这些像元的数字值和反射率,使用最小二乘的方法可以计算出每个波段的增益和偏置。
2) 光谱余弦值计算。
从地面样本中选取出修正地物,并在影像中选择其对应的像元,获得数字值,利用步骤1)中方法计算出的各波段增益和偏置,带入一个修正地物的数字值,计算出预测反射率, 记为ρ′(预测值)。计算预测值ρ′与地物真实测量值ρ之间的光谱角余弦值记为α, 光谱角余弦值的计算式[16]如式(2)所示。
| $ \cos \theta=\frac{\sum\limits_{i=1}^{n} \rho_{i}^{\prime} \rho_{i}}{\sqrt{\sum\limits_{i=1}^{n} \rho^{\prime 2}_ i} \sqrt{\sum\limits_{i=1}^{n} \rho_{i}^{2}}}, \theta \in\left[0, \frac{\pi}{2}\right] $ | (2) |
式中,cosθ是光谱角的余弦值α;ρ′i为修正地物第i波段的预测值;ρi为修正地物第i波段的真实测量值。
3) 定标参数的修正。
定标参数的修正是根据光谱角余弦值以及光谱预测值和真实测量值的差异来决定的。修正算法特点如下:预测值减去真实测量值的差值大于零,那么要使修正过程中预测光谱逼近真实测量的光谱,就应该让预测值慢慢变小,靠近真实测量值[17]。无人机12个波段的增益Gi都是大于0的数值,偏置Bi都是小于0的数值,各地物光谱角余弦值α均小于1。根据式(1)可以知道,要想预测值减小,则只需要增益减小,偏置增大,所以Gi·α使增益减小,Bi/α使偏置增大,这样预测值就会减小,逼近真实测量值;预测值减去真实测量值的差值小于零,则与预测值减去真实测量值的差值大于零的情况相反,所以需要Gi/α使增益增大,Bi·α使偏量减小,这样预测值就会增大,逼近真实测量值。
光谱角余弦值作为修正参数,是因为对于增益和偏置的修正,每次修正应该是一个比较小的改变,这样不会使修正后的增益和偏置变化太大,也不会使地物光谱变化太大,改变地物光谱规律。本研究中地物光谱角余弦值一般很接近1,用增益和偏置与一个接近于1的数值进行乘除运算,满足使他们变化很小的要求。
具体操作如下:利用步骤2)中计算出修正地物的预测值和真实测量值做减法运算,若预测值减去真实测量值的差值大于零,则需要Gi·α,Bi/α;若预测值减去真实测量值的差值小于零,则需要Gi/α,Bi· α,修正后的增益记为G′i,偏置记为B′i。此时,修正后的定标参数为G′i和B′i,利用修正后的定标参数更新步骤1)最小二乘计算出的定标参数,代入步骤2)、步骤3)中进行循环,循环结束的条件为光谱预测值已经最佳逼近真实测量值时,最佳逼近是指下次再迭代进行过后预测值ρ′与地物真实测量值ρ之间计算光谱角余弦值已经逼近1或者3次循环后光谱角余弦值的变化特别小,可忽略不计。
当循环结束时,代表这个修正地物的使命完成,将最后一次循环修正后的定标参数进行记录,更新步骤1)中的定标参数,然后从地面样本中选取出新的一个修正地物,并在影像中选择其对应的像元,获得数字值,代入步骤2)、步骤3)中进行新一轮的循环,新一轮循环结束时,修正后的定标参数同样需要更新步骤1)中的定标参数。
当所有修正地物都进行了修正,最后得到的定标参数即为本研究中修正后的最终定标参数。
4) 无人机影像辐射定标。
本实验中,利用步骤3)中最终定标参数,根据步骤1)中的式(1),可以将无人机影像转换为地表反射率产品。
1.3 其他辐射定标方法为了评价本文提出的方法,在同一幅无人机影像中还应用了经验线性回归方法。经验线性回归方法利用定标毯的数字值和反射率建立了影像数字值与反射率的关系,然后利用式(1)将同一幅无人机数字影像转换为地表反射率产品。
1.4 精度验证本文使用相对误差、平均相对误差作为精度验证标准,相对误差计算公式为:
| $ \varepsilon=\frac{\left|\rho^{\prime}-\rho\right|}{\rho} $ | (3) |
| $ \bar{\varepsilon}=\frac{1}{n} \sum\limits_{i=1}^{n} \frac{\left|\rho_{i}^{\prime}-\rho_{i}\right|}{\rho_{i}} $ | (4) |
式中,ρ′为无人机反演的地表反射率;ρ为对应的地表测量反射率;ρ′i为第i波段的无人机反演的地表反射率;ρi为第i波段的地表测量反射率;n为波段数。
2 结果与分析针对辐射定标后生成的地表反射率数据,分别对光谱余弦修正法(radiometric correction with spectral angle consine,RCSC)和经验线性回归法(empirical linear regression,EL)进行定标结果对比分析。
2.1 全部地物修正效果分析本文选取绿砖、马路、水体、植被、塑胶跑道、地板作为修正地物,在所有地物一起进行修正时,分析其修正后的精度。验证数据源于§1.1中所采集的地物标准反射光谱,根据无人机传感器波段,将ASD数据运算至相应波段,作为验证数据。
图 1显示了若干种典型地物的地面验证数据和两种校正方法得到的无人机影像反射率对比。可以看出对绿砖、马路、地板有相似的校正效果,而对水体、植被、塑胶跑道等地物,光谱余弦修正法校正后光谱曲线更加接近真实形态。
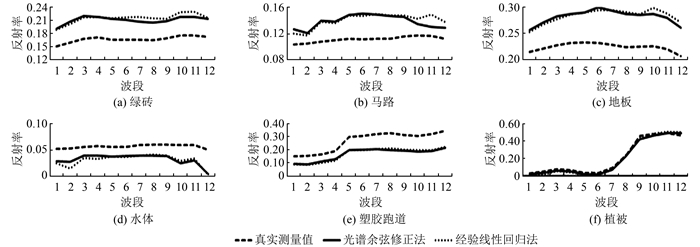 |
| 图 1 UAV影像地物光谱曲线对比 Fig.1 Comparison of Spectral Curves of UAV Image |
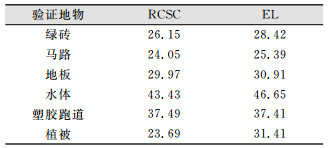
在光谱曲线的基础上,本文还定量分析了各地物两种方法相对误差的比较,如表 1所示。结果表明,在各地物中,两种方法都可以取得较好的效果,但是光谱余弦修正法的平均相对误差较低,精度较高。
| 表 1 各地物两种方法相对误差对比/% Tab.1 Comparison of Relative Error in Various Samples by RCSC and EL Methods/% |
 |
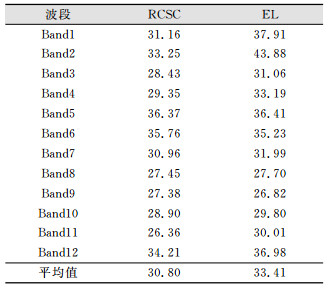
本文还对无人机影像在不同波段使用两种校正方法的校正精度进行了评估,结果如表 2所示。结果表明,各波段校正精度光谱余弦修正法优于经验线性回归法。光谱余弦修正法的平均相对误差比经验线性回归法降低了2.61%。
| 表 2 UAV影像校正相对误差统计/% Tab.2 Relative Calibration Error Statistics for UAV Image/% |
 |
2.2 不同地物修正效果分析
针对实验结果,本文还利用单一地物进行修正,分析单一地物修正时,对其他地物的影响效果。表 3显示了在单一地物进行修正时,在光谱余弦修正法下各地物的平均相对误差。
| 表 3 不同修正地物下各验证地物相对误差/% Tab.3 Relative Calibration Error Statistics for Various Samples/% |
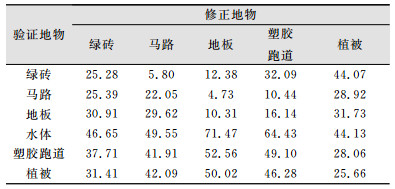 |
表 3中各地物相对误差与表 2中各地物在经验线性模型下的相对误差对比的结果表明:利用绿砖作为修正地物,绿砖、马路、地板在本文的光谱余弦修正法下,平均相对误差降低,而水体、塑胶跑道、植被的平均相对误差升高;利用马路作为修正地物,绿砖、马路、地板在本文的光谱余弦修正法下,平均相对误差降低,而水体、塑胶跑道、植被的平均相对误差升高;利用地板作为修正地物,绿砖、马路、地板在本文的光谱余弦修正法下,平均相对误差降低,而水体、塑胶跑道、植被的平均相对误差升高;利用塑胶跑道作为修正地物,水体、塑胶跑道、植被在本文的光谱余弦修正法下,平均相对误差降低,而绿砖、马路、地板的平均相对误差升高;利用植被作为修了地物,水体、塑胶跑道、植被在本文的光谱余弦修正法下,平均相对误差降低,而绿砖、马路、地板的平均相对误差升高。
根据本文光谱余弦修正算法的特点,结合不同地物作为修正时,各地物两种方法相对误差对比结果可以发现:分别以绿砖、马路、地板作为修正地物时,绿砖、马路、地板的精度得到了提高,而水体、塑胶跑道、植被的精度有所降低;分别以塑胶跑道、植被作为修正地物,水体、塑胶跑道、植被的精度得到了提高,而绿砖、马路、地板的精度有所降低。
由此可以发现,绿砖、马路、地板之间互相影响,会使他们的精度得到提高,水体、塑胶跑道、植被之间互相影响,也使精度提高。分析图 1中各地物光谱曲线,可以发现绿砖、马路、地板的预测光谱值大于真实测量光谱值;水体、塑胶跑道、植被的预测光谱值都小于真实测量光谱值。结合本文算法,可以得出结论,各地物对模型的修正结果主要取决于两个方面的原因:①地物光谱间的相似性;②地物光谱预测值与真实测量值之间的差异。当不同地物间满足光谱曲线形态相似且预测光谱值与真实测量光谱值之间的大小关系相同,在使用本文的光谱余弦修正法进行辐射校正时,就可以互相作为修正地物,提高其精度。基于以上分析,将本文的6个经典地物划分为两类,记为A类和B类,其中A类代表绿砖、马路、地板;B类代表水体、塑胶跑道、植被。
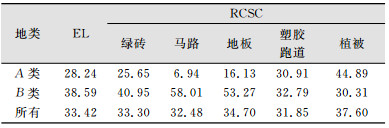
本文统计了对不同地物作为修正时,A类、B类、全部地物在光谱余弦修正法和经验线性回归法校正时的平均相对误差,如表 4所示。从表 4可以发现,正如以上分析的结果一样,绿砖、马路、地板单独作为修正,A类地物的精度提高,B类地物的精度下降;塑胶跑道、植被单独作为修正,A类地物的精度下降,B类地物的精度提高。
| 表 4 不同地物作为修正UAV影像校正相对误差统计/% Tab.4 Relative Calibration Error Statistics for Different Categories of Samples for UAV Image/% |
 |
3 结束语
随着遥感技术的发展,对遥感影像的精度提出了更高的要求。本文针对无人机影像的辐射校正提出了一种新的兼顾光谱信息的辐射校正方法,能有效解决无人机遥感影像辐射校正的问题,提高校正精度。通过本文光谱余弦角修正法和经验线性回归方法的对比,证明光谱余弦角修正法能有效提高辐射校正精度。本实验中的6种典型地物,在光谱余弦角修正法下,从无人机影像得到的反射率光谱总能与地面真实测量光谱形态更相似且更靠近。本文光谱余弦角法充分利用了被传统辐射校正忽视的各谱段间关系,从而得到了更加精准的校正模型,为辐射校正提高了一个新的思路。本方法不仅在无人机影像辐射校正时可以应用,在卫星影像辐射校正时也是一个应用方向。
| [1] |
龚建周, 夏北成. 基于大气辐射校正的广州市植被覆盖度遥感估算[J]. 应用生态学报, 2007, 18(3): 575-580. DOI:10.3321/j.issn:1001-9332.2007.03.020 |
| [2] |
陈挚秋, 王建力. 2015年夏秋季重庆市大气颗粒物污染与降水的关系[J]. 三峡生态环境监测, 2016, 1(1): 46-51. DOI:10.3969/j.issn.2096-2347.2016.01.007 |
| [3] |
Hu C, Muller-Karger F E, Andrefouet S, et al. Atmospheric Correction and Cross-Calibration of Landsat 7/ETM+Imagery over Aquatic Environments: A Multiplatform Approach Using SeaWiFS/MODIS[J]. Remote Sensing of Environment, 2001, 78(1/2): 99-107. |
| [4] |
Pahlevan N, Lee Z, Wei J, et al. On-orbit Radiometric Characterization of OLI (Landsat 8) for Applications in Aquatic Remote Sensing[J]. Remote Sensing of Environment, 2014, 154: 272-284. DOI:10.1016/j.rse.2014.08.001 |
| [5] |
谭金石, 黄书华, 黄正忠. 基于无人机遥感的海岛礁监测技术研究[J]. 测绘地理信息, 2018, 43(6): 55-57. |
| [6] |
任文艺, 伍丹, 秦林. 无人飞艇低空高光谱遥感数据采集与处理初探[J]. 三峡生态环境监测, 2016, 1(1): 52-57. DOI:10.3969/j.issn.2096-2347.2016.01.008 |
| [7] |
朱绍攀, 陈宇. 大气辐射校正方法分析[J]. 地理空间信息, 2010, 8(1): 113-116. DOI:10.3969/j.issn.1672-4623.2010.01.038 |
| [8] |
高海亮, 顾行发, 余涛, 等. 星载光学遥感器可见近红外通道辐射定标研究进展[J]. 遥感信息, 2010, 25(4): 117-128. DOI:10.3969/j.issn.1000-3177.2010.04.022 |
| [9] |
López D H, García B F, Piqueras J G, et al. An Approach to the Radiometric Aerotriangulation of Photogrammetric Images[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2011, 66(6): 883-893. |
| [10] |
Naughton D, Czaplamyers J S. Absolute Radiometric Calibration of the RapidEye Multispectral Imager Using the Reflectance-Based Vicarious Calibration Method[J]. Journal of Applied Remote Sensing, 2011, 5(1): 3 544-3 550. |
| [11] |
黄妙芬, 邢旭峰, 宋庆君, 等. 反射率基法获取北京一号小卫星多光谱CCD辐射定标系数[J]. 资源科学, 2009, 31(3): 509-514. DOI:10.3321/j.issn:1007-7588.2009.03.023 |
| [12] |
勾志阳, 晏磊, 陈伟, 等. 无人机高光谱成像仪场地绝对辐射定标及验证分析[J]. 光谱学与光谱分析, 2012, 32(2): 430-434. DOI:10.3964/j.issn.1000-0593(2012)02-0430-05 |
| [13] |
张勇, 顾行发, 余涛, 等. 中巴地球资源卫星热红外通道的交叉辐射定标[J]. 红外与毫米波学报, 2006, 25(4): 261-266. DOI:10.3321/j.issn:1001-9014.2006.04.005 |
| [14] |
孔祥兵, 舒宁, 陶建斌, 等. 一种基于多特征融合的新型光谱相似性测度[J]. 光谱学与光谱分析, 2011, 31(8): 2 166-2 170. |
| [15] |
汪小钦, 王苗苗, 王绍强, 等. 基于可见光波段无人机遥感的植被信息提取[J]. 农业工程学报, 2015, 31(5): 152-159. DOI:10.3969/j.issn.1002-6819.2015.05.022 |
| [16] |
魏祥坡, 余旭初, 付琼莹, 等. 光谱角余弦与相关系数测度组合的光谱匹配分类方法与实验[J]. 地理与地理信息科学, 2016, 32(3): 29-33. DOI:10.3969/j.issn.1672-0504.2016.03.006 |
| [17] |
万意, 李长春, 赵旭辉, 等. 基于SVM的光学遥感影像分类与评价[J]. 测绘地理信息, 2018, 43(6): 74-77. |
 2021, Vol. 46
2021, Vol. 46


