| 利用三维点云数据计算单木树冠体积的扇形分割算法 |
2. 武昌理工学院城市建设学院,湖北 武汉,430223;
3. 武汉大学测绘学院,湖北 武汉,430079
2. School of Urban Construction, Wuchang University of Technology, Wuhan 430223, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
三维激光扫描技术为不规则物体的建模和体积量算提供了一种方便可靠的途径[1-3]。在林业应用中,三维激光扫描技术不仅可用于树木的三维建模,还可以用来测量树冠冠幅、体积等参数,为评估树木生长状况、生态效益提供基础数据[4, 5]。基于三维点云数据的树冠体积计算方法从原理上主要可分为两类:体元法和切片法。体元法把三维空间划分为一系列等体积小立方体(体元),统计包含点云数据的有效体元个数即可得到树冠体积[6, 7]。切片法将树冠等间隔分割成许多个切片,按一定方法计算每个切片的体积后再累加得到树冠体积。切片法的关键是计算树冠横截面面积,根据截面积计算方法切片法又有多种算法,如圆台(锥)体算法[8]、凸包算法[4]和改进凸包算法[9]等。此外,还有直接对树冠整体进行三维建模来计算体积的方法[6, 10]。各种算法都有一定的优缺点,得到的树冠体积可能会有较大差异。本文基于扇形分割的截面积算法给出了一种树冠体积计算方法,并利用实测点云数据进行试验,与凸包算法和体元法进行对比验证。
1 单木树冠体积计算方法 1.1 扇形分割法本文提出的体积计算方法基于切片法。切片法的原理是将树木点云数据沿垂直方向等间隔分层,如图 1(a)所示,把每一层近似看成台体,累加各层台体的体积得到树冠体积,具体计算公式为[5]:
| $ V=\frac{\Delta h}{3} \sum\limits_{i=1}^{n-1}\left(S_{i}+\sqrt{S_{i} S_{i+1}}+S_{i+1}\right) $ | (1) |
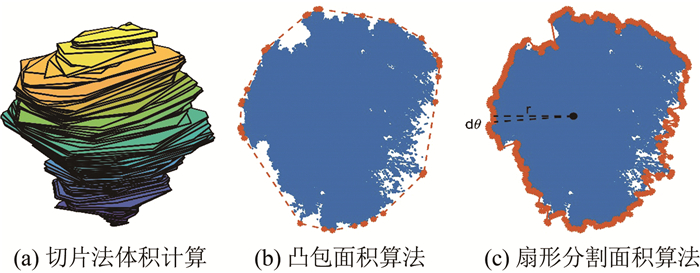 |
| 图 1 切片法体积计算原理 Fig.1 Schematic Diagram of Volume Calculation by Slices |
式中,n为切片的层数;Si为第i层切片的面积;Δh是分层的高度。式(1)显示切片法计算体积需要计算一系列树冠截面的面积,因此,体积计算的准确性主要取决于面积计算的准确性。常用的切片面积计算方法是凸包法,如图 1(b)所示,即把包含切片内全部点云的最小凸多边形的面积作为切面面积。然而,实际中很多的树冠切面并非凸多边形,此时,凸包算法会将树冠外围凹陷部分计入面积结果中,导致切片面积和树冠体积计算结果比实际值偏大。
为了克服凸包法的缺点,本文给出了一种基于扇形分割面积算法的树冠体积计算方案。扇形分割面积算法的基本原理如图 1(c)所示,以切片中心为极点,将切面等分为m个小扇区,则扇形的顶角dθ=2π/m,以扇区中最远数据点的极距作为小扇形的半径r,进而可计算得到每个小扇形的面积[11]。这些小扇形的面积之和即为切面面积:
| $ S_{i}=\sum\limits_{j=1}^{m} \frac{1}{2} r_{j}^{2} \mathrm{~d} \theta $ | (2) |
连接每个小扇区中的最远数据点可得到切面的外轮廓,图 1(b)和图 1(c)显示扇形分割法得到的外轮廓要比最小凸多边形更接近切面的实际外形,因而相应的面积计算精度要优于凸包法[11]。
1.2 体元法为了比较体积计算结果,本文还采用了体元法。其基本思想是将树冠视为由许多个给定大小的小立方体组成,因而将体积的计算转换为统计小立方体的数量,如图 2所示。基本步骤是:根据点云数据的空间范围将树冠周围空间划分为一个个立方体,统计出包含有点云数据的小立方体的数量,再乘上立方体的体积就得到了树冠的体积[6]。小立方体(体元)边长是体元法中的关键参数。体元设置太小将增加巨大的运算量,同时也可能使叶面缝隙的空间因没有点云数据而未计算在内,导致计算的体积偏小。体元太大则可能使树冠外轮廓严重偏离真实形状,导致计算结果偏大。文献[7]为体元边长的取值提供了一个经验准则。
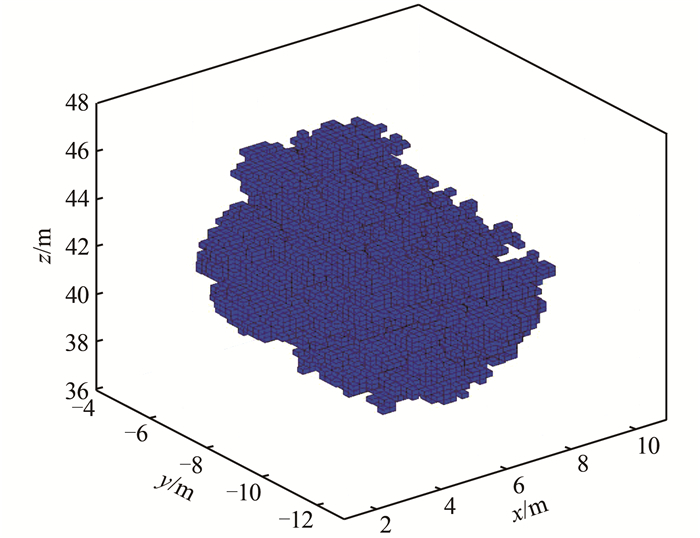 |
| 图 2 体元法示意图 Fig.2 Schematic Diagram of Voxel Mothed |
2 实验结果与分析
利用三维激光扫描仪在某校园采集了15株樟树的点云数据,树冠形态有较大差异。原始数据经过点云配准、滤波和去噪等预处理后,形成单株树木的点云数据,如图 3所示。
 |
| 图 3 实验树木点云数据 Fig.3 Point Cloud Data of Trees in this Study |
由于树冠体积真值未知,无法评估算法的绝对精度,本文将扇形分割法树冠体积计算结果与凸包法和体元法计算结果进行比较分析。计算体积时,扇形分割法、凸包法的高度分层高度为0.2 m,扇形分割法中m值设为300,体元法的体元边长取值为0.1 m。结果如图 4所示,3种方法中凸包法计算的体积值最大,体元法最小,扇形分割法介于凸包法和体元法之间,这一结果符合各算法的特点。凸包法将凸多边形与树冠实际轮廓之间的空隙包括在内,因而计算体积值偏大,而体元法则因未计入树冠内部真实空隙或由于枝叶遮掩产生的伪空隙导致结果偏小[6, 9]。
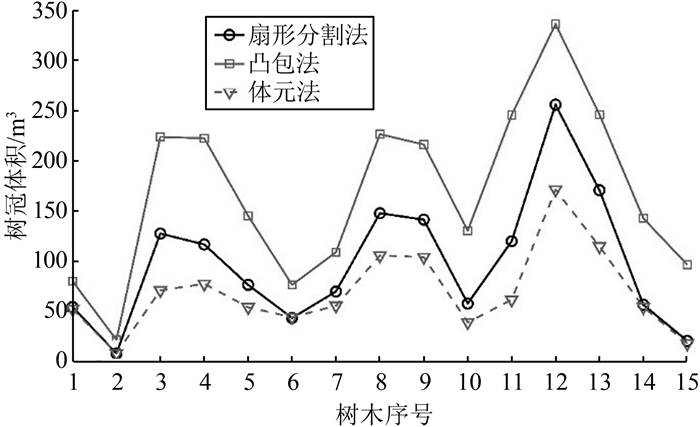 |
| 图 4 3种方法计算的树冠体积 Fig.4 Tree Crown Volumes Calculated by Three Methods |
不同方法的结果数值上存在较大差异,但存在很好的相关性。图 5中的线性回归模型显示,扇形分割法与其他两种方法的回归模型决定系数(R2)超过0.9,而凸包法和体元法之间R2值只有0.78。3种方法结果之间的皮尔森相关性分析也表明,本文方法与凸包法、体元法之间具有强相关性,相关系数分别为0.95(p < 1×10-7)和0.97(p < 1×10-9)。凸包法和体元法之间的相关系数为0.88(p < 1×10-4)。
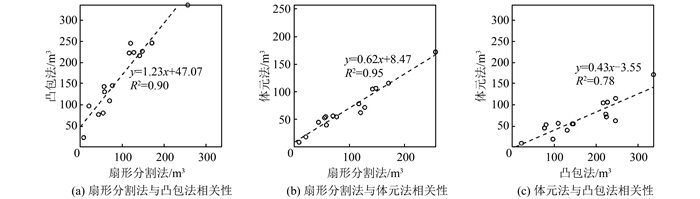 |
| 图 5 3种方法计算结果的线性回归模型 Fig.5 Linear Regression Models Between Results from Three Methods |
3 结束语
利用三维点云数据计算树冠体积,不同方法的结果有较大差异,这些差异源于方法本身的特点,很难简单评价某一方法更优。本文基于扇形分割算法提出了一种改进的体积计算方法,通过与凸包法、体元法进行对比,验证了新方法的有效性。实验表明新方法得到的树冠体积值介于凸包法和体元法之间,且具有强相关性。扇形分割法能有效克服传统凸包法因未剔除树冠外围凹陷空间导致体积偏大的不足,也可避免体元法未顾及枝叶遮蔽形成的伪空隙致使体积偏小的问题。
| [1] |
史向阳. 室内激光点云的三维场景快速重建[J]. 测绘地理信息, 2019, 44(1): 115-117. |
| [2] |
张荣华, 李俊峰, 林昀. 三维激光扫描技术在体积量算中的应用研究[J]. 测绘地理信息, 2014, 39(6): 47-49. |
| [3] |
刘明学, 崔进业. 基于点云三维坐标数据计算复杂物体体积[J]. 测绘地理信息, 2018, 43(3): 96-98. |
| [4] |
冯仲科, 罗旭, 马钦彦, 等. 基于三维激光扫描成像系统的树冠生物量研究[J]. 北京林业大学学报, 2007, 29(S2): 52-56. |
| [5] |
徐伟恒, 冯仲科, 苏志芳, 等. 一种基于三维激光点云数据的单木树冠投影面积和树冠体积自动提取算法[J]. 光谱学与光谱分析, 2014, 34(2): 465-471. |
| [6] |
Fernández-Sarría A, Martínez L, Velázquez-Martí B, et al. Different Methodologies for Calculating Crown Volumes of Platanus Hispanica Trees Using Terrestrial Laser Scanner and a Comparison with Classical Dendrometric Measurements[J]. Computers and Electronics in Agriculture, 2013, 90: 176-185. DOI:10.1016/j.compag.2012.09.017 |
| [7] |
韦雪花, 王永国, 郑君, 等. 基于三维激光扫描点云的树冠体积计算方法[J]. 农业机械学报, 2013, 44(7): 235-240. |
| [8] |
熊妮娜, 王佳, 罗旭, 等. 一种基于三维激光扫描系统测量树冠体积方法的研究——以油松为例[J]. 北京林业大学学报, 2007(S2): 61-65. |
| [9] |
董亚涵, 李永强, 李鹏鹏, 等. 基于改进凸包算法的树冠轮廓点提取与体积计算[J]. 测绘工程, 2018, 27(8): 66-71. |
| [10] |
李庆, 高祥伟, 费鲜芸, 等. 利用Alpha-shape算法进行树冠三维模型构建[J]. 测绘通报, 2018(12): 91-95. |
| [11] |
李宏星, 欧阳玉华. 基于三维激光扫描点云的树冠面积快速精准计算方法[J]. 绿色科技, 2015(6): 72-74. |
 2021, Vol. 46
2021, Vol. 46


