测绘地理信息   2019, Vol. 44 Issue (5): 8-10
0
引用本文
郑肇葆, 郑宏. 基于图像信息熵的高光谱图像分类[J]. 测绘地理信息, 2019, 44(5): 8-10. DOI:10.14188/j.2095-6045.2019165
ZHENG Zhaobao, ZHENG Hong. Hyperspectral Image Classification Based on Image Information Entropy[J]. Journal of Geomatics 2019, 44(5): 8-10. DOI:10.14188/j.2095-6045.2019165
基于图像信息熵的高光谱图像分类[PDF全文]
郑肇葆1, 郑宏2    
1. 武汉大学遥感信息工程学院，湖北 武汉，430079;
2. 武汉大学电子信息学院，湖北 武汉，430072
收稿日期: 2019-04-01
基金项目: 深圳市基础科研项目(JCYJ20150422150029095)
第一作者简介: 郑肇葆，教授，现主要从事摄影测量与遥感的教学和科研工作。E-mail:zhengzb@whu.edu.cn
摘要: 首先将一幅100像元×100像元的高光谱图像划分为以5像元×5像元构成的区域，作为大像元的图像，大像元中25个像元特征值的均值作为一个大像元的特征值。每组图像有175幅图像，实验中将他们分成四段，发现第三、四段的信息熵较小(其数值仅为二或三位数的数量级)，仅用第一、二段的数据进行分类。选用图像信息熵≥1 500的图幅，进行该类图像信息熵均值的计算。农田、山体、居民地、水体4类不同地物的信息熵的均值和4种地物中某个地物的属性，利用其信息熵值与4种不同地物信息熵的均值比较，差值最小者的属性，即为待定地物的属性。
关键词: 图像信息熵     高光谱图像分类     大像元    
Hyperspectral Image Classification Based on Image Information Entropy
ZHENG Zhaobao1, ZHENG Hong2    
1. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China;
2. School of Electronic Information, Wuhan University, Wuhan 430072, China
Abstract: Firstly, a hyperspectral image of 100×100 pixels is converted into a region composed of 5×5 pixels, as a large pixel image, the mean of the eigenvalues of 25 pixels in a large pixel is regarded as the eigenvalue of a large pixel.The information entropy of a hyperspectral image is obtained on the basis of a large pixel image.There are 175 images in each group. In the experiment, they are divided into four segments. It is found that the information entropy of the third and fourth segments are smaller (their value is only the order of magnitude of two or three digits), only the data in the first and second segments are adopted. We choose the images whose information entropy is more than 1 500, and calculate the mean value of information entropy of this kind of images. There are four kinds of different land objects whose mean information entropy are known: farmland, mountain, residential area and water area. To determine the attributes of a certain land object in the four, we compare its information entropy with the mean values of information entropy of four different land objects, and the attributes of the smallest difference are that of the land object to be determined.
Key words: image information entropy     hyperspectral image classification     large image pixels    

众所周知，在航空摄影的图像分类中，高光谱图像与航空摄影图像不完全相同。高光谱图像在空中摄影时，在空中一个位置不是摄取地面一张像片，而是由几百张具有不同波段的像片组成的。实验中使用的高光谱图像，摄影一次就有242张像片，因为它有242个不同的波段，每个波段有一张像片。在空中一个位置摄取的242张像片称为一组，如果在空中n个位置对地面同一类型目标进行摄影，则获取n组高光谱图像，每一组有242张不同波段的高光谱图像。笔者在实验中使用4种不同类型的高光谱图像：农田(12组)、山体(15组)、居民地(11组)、水体(12组)，利用图像的信息熵[1]来进行高光谱图像的分类。

1 高光谱图像的信息熵

在高光谱图像分类中，为了节省计算信息熵的时间，将一幅100像元×100像元图像划分为若干5像元×5像元，并把每个像元块称为“大像元”，用大像元中25个像元的灰度均值作为一个“大像元”的特征值。假定一幅图像中每个大像元的特征为f(i, j)，求得该幅图像的大像元特征均值为fcp，可以得到每个大像元的残差v(i, j)和该幅图像特征的标准差[1]。

在这个基础上，将一幅大像元图像分为两组：第一组是大像元特征值f(i, j)与该图像大像元特征的均值fcp之差的绝对值小于或等于2 m的n1个大像元组成。第二组大像元数量为n2=n-n1。

可以得到适用的图像信息熵[1]：

$H = P\left( {{a_1}} \right)I\left( {{a_1}} \right) + P\left( {{a_2}} \right)I\left( {{a_2}} \right) $

式中，H表示一幅图像的信息熵；P(a1)表示第一组大像元的先验概率；P(a2)表示第二组大像元的先验概率；I(a1)和I(a2)分别表示第一、二两组大像元的特征均值。

实验数据有4种不同地形特征：农田、山体、居民地、水体，每组图像有242幅(每个波段一幅图像)，经过筛选，保留175幅图像供研究使用。将175幅图像分成4段(0~49，50~93，94~133，134~174)，对4类不同地形的每幅图像作了以下分析研究：

1) 第一段(0~49)：H≥2 000的个数为40个；1 500≤H < 2 000的个数为7个；1 000≤H < 1 500的个数为3个。

2) 第二段(50~93)：H≥2 000的个数为16个，其中≥3 000的4个；1 500≤H < 2 000的个数为12个；1 000≤H < 1 500的个数为8个。

3) 第三段(94~133)：H≥2 000的个数为0个；1 500≤H < 2 000的个数为0个；1 000≤H < 1 500的个数为0个。

4) 第四段(133~174)：按同样3个区间段作信息熵的统计情况，全是零。

从以上175幅图像信息熵的分布情况可知：第三、四段图像的信息熵仅为二、三位十进制数字，有的甚至为零。鉴于这种情况，在以后的试验中，仅用第一段和第三段数据计算的结果。

2 高光谱图像的分类

高光谱图像在空中一个位置摄取了地面同一个目标242幅图像，经过筛选，我们使用其中175幅，这些图像与通常航空摄影得到的图像，主要差异是后者摄取的每张像片的波段都是相同的；而前者摄取的每张像片的波段是不相同的，尽管是对同一地面目标，高光谱图像的信息熵不完全相同，给目标的分类带来困难[2-18]。为了解决这个问题，关键是每个类别基准图像的选取，对于航空摄影的图像，通常对每个类别的图像选取1/3的图像作为该类别的基准图像，进行图像的分类[19-22]。这种方法对于高光谱图像的分类并不适用，因为高光谱图像在空中一个位置摄取了242幅不同波段的图像(在试验中采用了175幅)，每幅图像的信息熵不完全相同。信息熵的大小反映出图像信息量的多少，我们选用图像信息熵H≥1 500的有效，可以参加该图像信息熵均值的计算。在实验中每一组的第一段、第二段的信息熵均值就是这样得到的。将农田12组图像第一段、第二段的信息熵列在表 1中。

表 1 农田的信息熵 Tab.1 Information Entropy of the Farmland

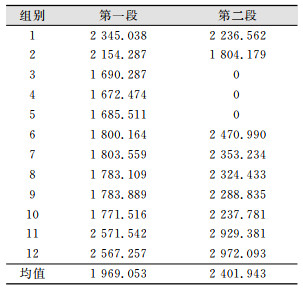类似地，对山体15组图像、居民地11组图像以及水体12组图像信息熵列表的最后一行也计算其相应的第一段、第二段信息熵的均值。这些数据在文中没有象农田(表 1)那样一一列出来。今有待定属性的一幅图像的信息熵(假定是第一段的)与4个类别第一段信息熵均值比较，其中差值绝对值最小的属性，即为待定图像的属性。如表 2所示。

表 2 各类别信息熵均值与某类个体信息熵的差值 Tab.2 Values Are the Difference Between the Information Entropy of Determing a Land Object and the Mean Values of Information Entropy of the Different Land Objects

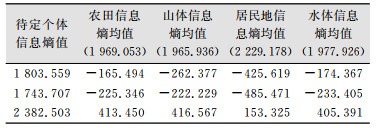表 2第1行中待定个体信息熵为1 803.559，它与4个类别各自的信息熵均值比较，最小的差值绝对值为165.494，该类的属性为农田，即可判定待定个体属性为“农田”。第2行待定个体信息熵为1 743.707，它与4个类别各自的信息熵均值比较，最小的差值绝对值为222.229，该类的属性为山体，即可判定待定个体的属性为“山体”。第3行待定个体信息熵为2 382.503，它与4个类别各自的信息熵均值比较，最小的差值的绝对值为153.325，该类的属性为居民地，即可判定待定个体的属性为居民地。

实验中使用农田12组、山体14组、居民地11组、水体12组高光谱图像，按前面介绍的图像分类方法进行分类实验，分类的结果为农田11/12、山体13/14、居民地11/11、水体11/12(分数、分母的数值表示每类场地的图像数，分子为相应地物图像被正确分类的数量)。

3 结束语

本文将一幅100像元×100像元的高光谱图像划分为以5像元×5像元构成的区域，作为大像元的图像，25个像元特征值的均值作为一个大像元的特征值。实验中将农田、山体、居民地、水体等4类不同地物每组图像的175幅图像分成4段，选用图像信息熵≥1 500的图幅有效，参加该类图像信息熵均值的计算。4种地物中某个地物的属性，利用其信息熵值与4种不同地物信息熵的均值比较，差值最小者的属性，即为待定地物的属性。

参考文献
[1]
郑肇葆, 郑宏. 基于图像信息熵的图像分类[J]. 测绘地理信息, 2018, 43(5): 1-3.
[2]
Zhang Xiangrong, Gao Zeyu, Jiao Licheng, et al. Multifeature Hyperspectral Image Classification with Local and Nonlocal Spatial Information via Markoo Random Field in Semantic Space[J]. IEEE Trans on Geoscience and Remote Sensing, 2018, 56(3): 1409-1424. DOI:10.1109/TGRS.2017.2762593
[3]
Zabalza J, Ren Jinchang, Wang Zheng, et al. Fast Implementation of Singular Spectrum Analysis for Effective Feature Extraction in Hyperspectral Imaging[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2845-2853. DOI:10.1109/JSTARS.2014.2375932
[4]
Zhao Wenzhi, Du Shihong. Spectral-Spatial Feature Extraction for Hyperspectral Image Classification:A Dimension Reduction and Deep Learning Approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4544-4554. DOI:10.1109/TGRS.2016.2543748
[5]
Wu Hao, Prasad S. Dirichlet Process Based Active Learning and Discovery of Unknown Classes for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4882-4895. DOI:10.1109/TGRS.2016.2552507
[6]
Chen Jike, Xia Junshi, Du Peijun, et al. Combining Retation Forest and Multiscale Segmentation for the Classification of Hyperspectral Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(9): 4060-4072. DOI:10.1109/JSTARS.2016.2524517
[7]
Sun Le, Wu Zebin, Liu Jianjun, et al. Supervised Spectral-Spatial Hyperspectral Image Classification with weighted Markoo Random Fields[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1490-1503. DOI:10.1109/TGRS.2014.2344442
[8]
Sun Bin, Kang Xudong, Li Shutao, et al. Random-Walker-Based Collaborative Learning for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 99: 1-11.
[9]
Xue Zhaohui, Du Peijun, Li Ju, et al. Sparse Graph Regularization for Hyperspectral Remote Sensing Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(4): 2351-2366. DOI:10.1109/TGRS.2016.2641985
[10]
吴银花, 胡炳樑, 高晓惠, 等. 利用区域增长技术的自适应高光谱图像分类[J]. 光学精密工程, 2018, 26(2): 426-434.
[11]
张会敏, 杨明, 吕静. 基于自适应核联合稀疏表示的多特征高光谱图像分类[J]. 中国科学技术大学学报, 2018, 48(4): 41-49.
[12]
田彦平, 陶超, 邹峥嵘, 等. 主动学习与图的半监督相结合的高光谱影像分类[J]. 测绘学报, 2015, 44(8): 919-926.
[13]
王君言, 张春梅, 张云斌, 等. 基于DL1图和KNN图叠加图的高光谱图像半监督分类算法[J]. 中国科学:信息科学, 2017(12): 66-77.
[14]
程志会, 谢福鼎. 基于空间特征与纹理信息的高光谱图像半监督分类[J]. 测绘通报, 2016(12): 59-62.
[15]
万源, 陈晓丽, 张景会, 等. 低秩稀疏图嵌入的半监督特征选择[J]. 中国图象图形学报, 2018(9): 1316-1325.
[16]
崔宾阁, 吴子宾, 秦学川, 等. 基于改进标签传播算法的高光谱图像半监督分类[J]. 山东科技大学学报(自然科学版), 2016, 35(6): 101-107. DOI:10.3969/j.issn.1672-3767.2016.06.016
[17]
李绣心, 凌志刚, 邹文. 基于卷积神经网络的半监督高光谱图像分类[J]. 电子测量与仪器学报, 2018(10): 95-102.
[18]
闫苗, 赵红东, 李宇海, 等. 基于卷积神经网络的高光谱遥感地物多分类识别[J]. 激光与光电子学进展, 2019, 56(2): 191-198.
[19]
郑加苏.基于图像信息熵的无参考图像质量评估算法的研究[D].北京: 北京交通大学, 2015
[20]
张钧萍, 张晔. 基于多特征多分辨率融合的高光谱图像分类[J]. 红外与毫米波学报, 2004, 23(5): 345-348. DOI:10.3321/j.issn:1001-9014.2004.05.007
[21]
樊利恒, 吕俊伟, 于振涛, 等. 基于核映射多光谱特征融合的高光谱遥感图像分类法[J]. 光子学报, 2014, 43(6): 87-92.
[22]
刘峰, 龚健雅. 一种基于多特征的高光谱遥感图像分类方法[J]. 地理与地理信息科学, 2009(3): 19-22.