| 三维空间基准转换公共点选取的新方法 |
2. 地球空间信息技术协同创新中心,湖北 武汉,430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
WGS-84坐标转化为西安80坐标系下的坐标,涉及到三维空间的基准转换。而七参数是不同的空间直角坐标系之间坐标转换的必要参数,包括三个平移参数、三个旋转参数和一个尺度参数[1, 2]。七参数可以直接从测绘部门获得,或利用至少3个公共点求得,因此,利用至少3个公共点求解七参数的过程中,公共点的选取将影响到坐标转换的精度。待求点离公共点距离越小,转换精度越高; 公共点分布越均匀,观测的公共点越多,则转换参数解算越稳定,解算精度也越高[3, 4]。但针对公共点处于不同的相对位置时,尤其是大区域下,如何选取均匀分布的公共点且兼顾待求点离公共点的距离小,并保证坐标转换精度能够达到最高还有待深入研究。
本文基于布尔沙-沃尔夫(Bursa-Wolf)模型,首先给出了坐标转换的主要公式,通过WGS-84坐标系与西安80坐标系的转换实例,将有效面积分析法引入某区域实测的两组GPS公共点位选取,提出了一种指导公共点选择的新方法,分析了不同空间域公共点的选择对坐标转换精度的影响关系。
1 三维空间基准转换原理将地心坐标系下的WGS-84坐标转换到参心坐标系下的西安80坐标,通常采用含有七参数的布尔沙-沃尔夫模型。工程测量中经常使用的是高斯投影平面坐标(x,y,h)[5],将WGS-84大地坐标(B, L, H)转换为空间直角坐标(X84, Y84, Z84),通过式(1)转换到西安80空间直角坐标(X80,Y80,Z80)[6],利用式(3)~式(5)得到西安80大地坐标(B, L, H),经高斯投影后得到平面坐标(x,y,h),坐标转换流程如图 1所示。
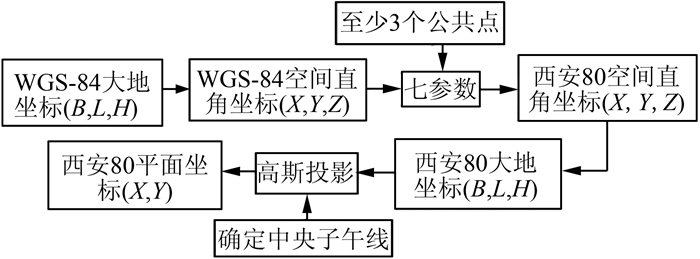 |
| 图 1 七参数法坐标转换流程图 Figure 1 Flow Chart of Seven-Parameter Transformation |
1.1 七参数法坐标转换原理
设点(X80, Y80, Z80)和(X84, Y84, Z84)分别表示西安80空间直角坐标和WGS-84空间直角坐标,布尔沙-沃尔夫七参数模型为[7]:
| $ \left[{\begin{array}{*{20}{c}} {{X_{80}}}\\ {{Y_{80}}}\\ {{Z_{80}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\Delta {X_0}}\\ {\Delta {Y_0}}\\ {\Delta {Z_0}} \end{array}} \right] + \left( {1 + m} \right)\left[{\begin{array}{*{20}{l}} 1&{{\varepsilon _Z}}&{-{\varepsilon _Y}}\\ {-{\varepsilon _Z}}&1&{{\varepsilon _X}}\\ {{\varepsilon _Y}}&{-{\varepsilon _X}}&1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{X_{84}}}\\ {{Y_{84}}}\\ {{Z_{84}}} \end{array}} \right] $ | (1) |
式中,ΔX0、ΔY0、ΔZ0为3个平移参数;εX、εY、εZ为3个旋转参数;m为尺度变化参数。这7个转换参数的求解需要知道至少3个公共点,当多于3个公共点时,按照最小二乘法求得7个参数的最或然值。
1.2 大地坐标与空间直角坐标的转换大地坐标转换到空间直角坐标公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {X = \left( {N + H} \right)\cos B\cos L}\\ {Y = \left( {N + H} \right)\cos B\sin L}\\ {Z = \left( {N\left( {1-{e^2}} \right) + H} \right)\sin B} \end{array}} \right. $ | (2) |
式中,卯酉圈曲率半径
空间直角坐标转换到大地坐标公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {L = \arctan \left( {Y/X} \right)}\\ {B = \arctan \left( {\frac{{Z + N{e^2}\sin B}}{{\sqrt {{X^2} + {Y^2}} }}} \right)}\\ {H = \sqrt {{X^2} + {Y^2}} \cdot \sec B-N} \end{array}} \right. $ | (3) |
大地纬度B的计算比较复杂,通常采用迭代法。迭代时,设置初值
本文提出的有效面积是指选取的公共点所围成的最大面积。假设有5个点,点号分别为1、2、3、4、5;当选取1、2、3点为公共点时,3个点依次连线所包围的最大面积即为有效面积。
有效面积分析法就是将有效面积和有效面积覆盖的测量点数量作为选取公共点的考虑因素,建立有效面积、有效面积覆盖的测量点数量与平面坐标转换精度的联系,研究其与平面坐标转换精度的关系。本文将转换点的点位标准差σ、x和y方向较差绝对值的平均值|Δx|和|Δy|作为指标来衡量有效面积分析法的可行性。其中,标准差的计算公式为:
| $ \sigma = \sqrt {\sum\limits_{i = 1}^n {\Delta s_i^2/n} }, \;\;\;\Delta {s^2} = \Delta {x^2} + \Delta {y^2} $ | (4) |
x和y方向较差绝对值的平均值为:
| $ \left| {\Delta \bar x} \right| = \frac{{\sum\limits_{i = 1}^n {\left| {\Delta {x_i}} \right|} }}{n}, \left| {\Delta \bar y} \right| = \frac{{\sum\limits_{i = 1}^n {\left| {\Delta {y_i}} \right|} }}{n} $ | (5) |
山东省某测区实测的两组GPS观测点,均已知西安80平面坐标(x,y,h)和WGS-84大地坐标(B, L, H),其中第一组数据精度高,如图 2(a)所示,最长基线为14.8 km,覆盖面积约为72.6 km2, 中央子午线为115°30′;第二组数据精度低,如图 2(b)所示,最长基线为23.3 km,覆盖面积约为154.5 km2, 中央子午线为120°。
 |
| 图 2 已知点位分布 Figure 2 Distribution of Known Points |
3.2 有效面积对转换精度的影响
1)数据处理。为了考虑有效面积对平面坐标转换精度的影响,对两组数据均采取选择3个点为公共点,剩余点为测量点的处理方法,每组有C52=10种组合结果,图 3分别给出了各组合点位图,表 1给出了有效面积对转换精度的影响。
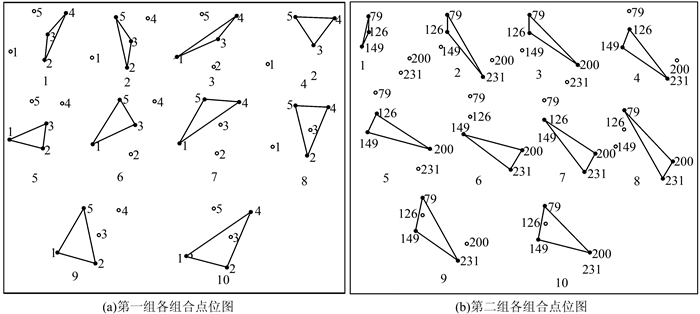 |
| 图 3 第一组和第二组各组合点位图 Figure 3 Points Distribution in Group 1 and Group 2 |
| 表 1 第一组和第二组有效面积对转换精度的影响 Table 1 Effects from Effective Area to Accuracy of Coordinate Transformation in Group 1 and Group 2 |
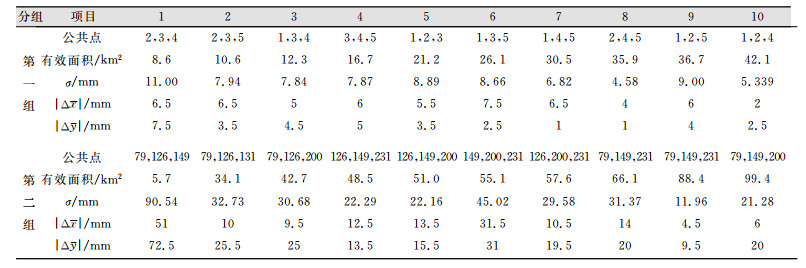 |
2)数据分析。转换点标准差随有效面积的变化如图 4中的折线所示,其规律可以用对数函数拟合,可以看出,转换点的点标准差围绕对数函数的下降趋势呈上下浮动。从表 1可见,σ、|Δx|、|Δy|从组合1到组合10整体呈下降趋势。随着有效面积的增大,σ、|Δx|、|Δy逐渐减小。表明有效面积增大,平面坐标转换精度得到提高。
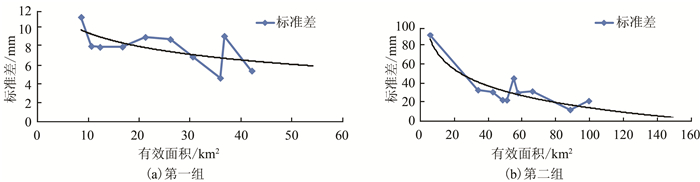 |
| 图 4 误差随有效面积的变化 Figure 4 Error with a Change of the Effective Area |
从表 1中第一组数据和图 3(a)可见,组合5、6、9的结果比较异常,是因为这3个组合的公共点都位于点位分布的一侧,测量点距离公共点较远,公共点分布很不均匀;与组合5、6、9相比较,组合2、3、8、10的公共点实现了均匀分布,随着有效面积增大,其坐标转换精度得到明显提高。而组合8、10与所有组合相比,有效面积大且覆盖了一定数量的测量点,所以其坐标转换精度最高。
从表 1中第二组数据和图 3(b)可见,组合6的测量点距公共点较远,公共点分布不均匀,所以其结果比较异常。组合5、9的公共点均匀分布,但组合9的有效面积明显大于组合5,因而其坐标转换精度明显好于组合5。而组合9、10的有效面积最大,且覆盖了一定数量的测量点,所以其坐标转换精度是最高的。
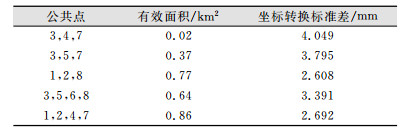
为了验证上述大区域(70~160 km2)得到的结论亦适用于小区域,本文特选取某小区域实例进行验证,如图 5所示。已知8个点,覆盖面积约1.6 km2,最长基线为2.0 km。顾及公共点均匀分布和覆盖测量点的数量,选取不同有效面积的5组公共点进行坐标转换,结果如表 2所示。可见,不论是选取3个公共点还是4个公共点,有效面积越大,坐标转换精度越高。
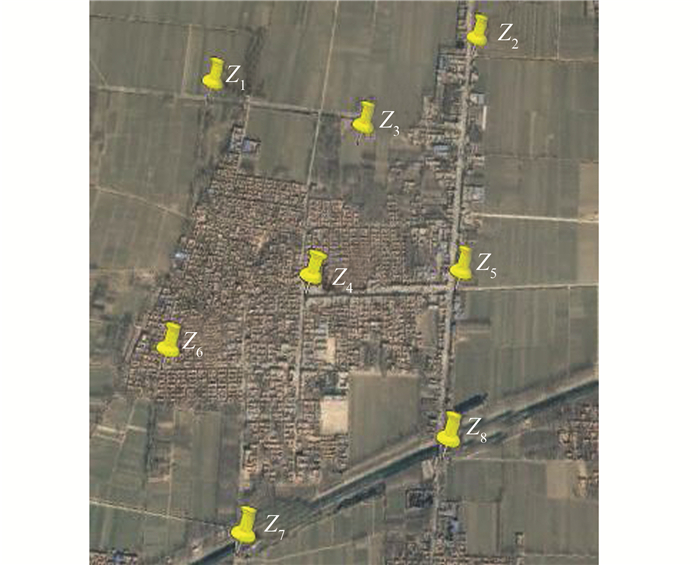 |
| 图 5 验证点点位分布图 Figure 5 Distribution of Verification Points |
| 表 2 验证结论 Table 2 Verification Conclusions |
 |
4 结束语
本文通过实例分析了不同公共点的选取对平面坐标转换精度的影响,验证了有效面积分析法指导公共点选取的可行性。实验结果证明,利用有效面积分析法指导公共点选择是合理且有效的;有效面积越大,坐标转换精度越高;在公共点分布均匀时,有效面积越大,有效面积覆盖的测量点数量越多,坐标转换精度越好。
| [1] |
王解先, 邱杨媛. 高程误差对七参数转换的影响[J].
大地测量与地球动力学,2007,27(3) : 25–28.
Wang Jiexian, Qiu Yangyuan. Influence of Ellipsoidal Height Error on Seven-Parameter Transformation[J]. Journal of Geodesy and Geodynamics,2007,27(3) : 25–28. |
| [2] |
谢鸣宇, 姚宜斌. 三维空间与二维空间七参数转换参数求解新方法[J].
大地测量与地球动力学,2008,28(2) : 104–109.
Xie Mingyu, Yao Yibin. A New Method for Solution of Seven-Parameter Transformation Between 3D and 2D Spaces[J]. Journal of Geodesy and Geodynamics,2008,28(2) : 104–109. |
| [3] |
王玉成, 胡伍生. 坐标转换中公共点选取对于转换精度的影响[J].
现代测绘,2008,31(5) : 13–15.
Wang Yucheng, Hu Wusheng. Influence Caused by Public Points Selection on Accuracy of Coordinate Conversion[J]. Modern Surveying and Mapping,2008,31(5) : 13–15. |
| [4] |
马腾, 王耀强, 葛岱峰, 等. 坐标转换参数及测点与公共点距离对手持GPS精度的影响[J].
测绘信息与工程,2010,35(5) : 16–17.
Ma Teng, Wang Yaoqiang, Ge Daifeng, et al. Influence of Transformation and Distance Parameters Between Common Point and Measuring Point on Accuracy of Mobile GPS[J]. Journal of Geomatics,2010,35(5) : 16–17. |
| [5] |
马家琼, 杨晓英, 崔文刚. WGS-84和西安80坐标转换研究[J].
测绘与空间地理信息,2013,36(4) : 158–160.
Ma Jiaqiong, Yang Xiaoying, Cui Wengang. The Research of Coordinate Transformation Between WGS-84 and Xi'an 80[J]. Geomatics and Spatial Information Technology,2013,36(4) : 158–160. |
| [6] |
黄太山. 浅谈常用坐标系统的关系及坐标转换的原理[J].
测绘与空间地理信息,2011,34(6) : 269–274.
Huang Taishan. Discussion on Relations of Commonly Used Coordinates System and the Principle of Coordinate Conversion[J]. Geomatics and Spatial Information Technology,2011,34(6) : 269–274. |
| [7] |
徐仕琪, 张晓帆, 周可法, 等. 关于利用七参数法进行WGS-84和BJ-54坐标转换问题的探讨[J].
测绘与空间地理信息,2007,30(5) : 33–42.
Xu Shiqi, Zhang Xiaofan, Zhou Kefa, et al. Discussion of Seven-Parameter Coordinate Transformation Between WGS-84 and BJ-54[J]. Geomatics and Spatial Information Technology,2007,30(5) : 33–42. |
 2016, Vol. 41
2016, Vol. 41

