| 一种基于SRTM高程数据的可视化选取投影面的新方法 |
随着2000中国大地坐标系(China geodetic coordinate system 2000, CGCS2000)的启用,各省市相继将地方相对独立的坐标系转换为CGCS2000椭球下的坐标系统[1, 2]。建立地方独立坐标系的传统方法是将城市以县区等经济发达地区为单位划分坐标系,将一个地区划分为多个独立坐标系,分别取其中央子午线为高斯投影中央子午线,平均海拔为投影面,建立高斯平面坐标系[3, 4]。这样做容易满足变形精度要求,却使一个地区存在多个独立坐标系。随着城市的发展,独立坐标系已经不能满足城市扩张的需求,急需建立统一的能够满足变形精度要求的坐标系。投影长度变形与投影面的高程和距离中央子午线的距离有关,建立与之相对应的独立坐标系的常用方法包括抵偿高程面法(改变投影面高程)、任意带法(改变投影的中央子午线)及将两者结合起来的方法(既改变投影面高程又改变投影的中央子午线)[5]。传统选取抵偿高程面的方法是结合测区的控制点高程数据,选取测区控制点的平均高程面或最高、最低高程的平均高程面为抵偿高程面,该方法操作简单,但是对于控制点的几何分布有较高要求,在那些海拔较高或地形起伏较大的地区,由于控制点稀少,且点位分布不均匀,缺少相应的高程值,造成抵偿高程面选取的不准确,导致部分地区产生较大的投影长度变形。本文提出了一种基于航天飞机雷达地形测绘任务(shuttle radar topography mission,SRTM)全球地形起伏数据的可视化选取投影面的方法,通过3″×3″(90 m×90 m)均匀的格网点获得测区较为全面的高程数据,计算投影变形及均方根(root mean square, RMS)值,根据RMS值最小原则,选择合适的投影高程面。与传统方法相比,该方法克服了高海拔地区或山区控制点少的缺点,并且可以利用GMT(generic mapping tools)软件将投影变形按区域直观地呈现出来,实现了投影面选取的可视化,有利于结合实际的地形条件及经济发展需要选取合适的投影面。
1 实验原理 1.1 投影变形计算原理采用测距仪等手段在地面量距,其观测边长D归算至参考椭球面上时,长度会缩短ΔD,设观测边的平均大地高为H′,地球平均曲率半径为R,则由此引起的高程归化改正有如下近似关系:
| $ \frac{{\Delta D}}{D} \approx \frac{{H'}}{R} $ | (1) |
椭球面上的边长S投影至高斯平面,其长度将放长ΔS,设该边两端点的平均横坐标为Ym,由此引起的高斯投影距离改正有如下近似关系式[6]:
| $ \frac{{\Delta S}}{S} = \frac{{Y_m^2}}{{2{R^2}}} $ | (2) |
式(1)和式(2)变形具有相互抵偿的地带,高程归化改正与高斯投影改正的差值σ为[7, 8]:
| $ \sigma = \left| {\frac{{H'}}{R} - \frac{{Y_m^2}}{{2{R^2}}}} \right| $ | (3) |
如果考虑投影长度变形的正负,则式(3)为:
| $ \sigma = \frac{{H'}}{R} - \frac{{Y_m^2}}{{2{R^2}}} $ | (4) |
为保证投影长度变形计算的精确性,可用投影点所在卯酉圈半径N替代上式中的地球平均半径R,计算公式为[9]:
| $ N = \frac{a}{W}, 可得\;\;W = \sqrt {1 - {e^2}{{\sin }^2}B} $ | (5) |
式中,e为椭球第一偏心率;a为椭球长半轴;B为投影点地理纬度。
在利用抵偿高程面法建立独立坐标系时,并未减小距离的高斯投影改正值(即式(2)表示的距离改正),而是选择一个合适的水准面来作为投影面,由此引起的高程归化值抵偿高斯投影改正值,在该面上,高程归化改正与高斯投影改正相互抵偿。高程归化改正与高斯投影改正的差值σ为[10, 11]:
| $ \sigma = \left| {\frac{{H - {H_0}}}{R} - \frac{{Y_m^2}}{{2{N^2}}}} \right| $ | (6) |
式中,H0为基准面高程值;H为点高程值,单位为m。
显然,若取测区的平均高程面作为投影面,则位于平均高程面上边长的高程归化改正值为零。为使测区中心处式(3)中两项改正值之和为零,则投影面比平均高程面低的部分H′m应具有如下数学关系:
| $ \frac{H_{m}^{'}}{N}-\frac{Y_{m}^{2}}{2{{N}^{2}}}=0,得\ \ H_{m}^{'}=\frac{Y_{m}^{2}}{2N} $ | (7) |
在利用任意带法建立独立坐标系时,由于高程归算面不变,故由式(1)表示的高程归化改正值不变,此时选择一条合适的子午线作为中央子午线,由此引起的边长的高斯投影改正抵偿高程归化改正值。
由式(7)可知,若取测区的平均高程面为投影面,则H′m=0,此时可得Ym=0,即取测区平均经线为中央子午线。顾及投影长度变形的符号,投影变形公式为:
| $ \sigma = \frac{{H - {H_0}}}{N} - \frac{{Y_m^2}}{{2{N^2}}} $ | (8) |
式中,当卯酉圈半径N取地球平均半径6 373.137km时,根据式(8)计算可以得到投影变形。县级区域的东西长度不超过100km,高斯投影距离改正相对较小,而高程对投影长度变形的影响相对较大。
1.2 投影面选取步骤1) 根据测区范围从相关主管部门获得测区边界数据或从全球行政区域边界数据(global administrative areas, GADM)库获取行政边界数据。
2) 从美国SRTM官网获取的SRTM地形数据,水平分辨率为90 m,数字高程精度为1 m,根据上一步获得的边界数据利用GMT软件进行裁切,绘制测区的数字高程模型(digital elevation model,DEM)。
3) 利用已有的坐标系参数和SRTM地形数据,根据绘制的测区DEM选择初始的投影面高程及步长,分别计算相应高程投影面下的区域投影变形,并计算其RMS值,利用GMT软件展绘在图上。
4) 依据不同高程面的投影变形分布图和相应的RMS值,结合实际情况,考虑地形因素选择合适的投影面。如果地形比较平坦则直接依据RMS值最小为原则选取投影面;如果地形起伏较大,则应依据平原、山谷等地区投影变形较小为原则选取投影面。
2 投影面选取实例1) 投影变形分析及数据来源。本文以湖北省武汉市独立坐标系投影面的选取为例来证明本文提出的投影面选取方法的可行性。武汉市地处江汉平原,地势较为平坦,平均海拔为40 m。由式(5)计算得到武汉地区的卯酉圈曲率半径N武汉≈6 378 km。由式(8)计算投影变形为:
| $ \sigma = \frac{{H - {H_0}}}{{6378}} - \frac{{{y^2}}}{{2 \times 6378 \times 6378}} $ | (9) |
式中,σ为点位投影变形,单位为cm;y为点在高斯投影面上的y坐标,即距离中央子午线的距离;根据式(9)计算可以得到,较大的高程变动会导致较大的投影变形。高程每变化63.78m,投影变形相应增加或减小1cm。如果需要投影变形在2.5cm之内,则高差(H-H0)必须在±159m范围内。市级区域的东西长度不超过100 km,影响不大。因此,设定坐标系最重要的是设置投影高程面。武汉市的行政边界数据从GADM库获取,高程数据采用SRTM的3″×3″的DEM数据。
2) 投影变形的计算及投影面的选取。利用GMT软件根据武汉市行政边界数据对其高程数据进行裁切,绘制武汉市的DEM,如图 1所示。
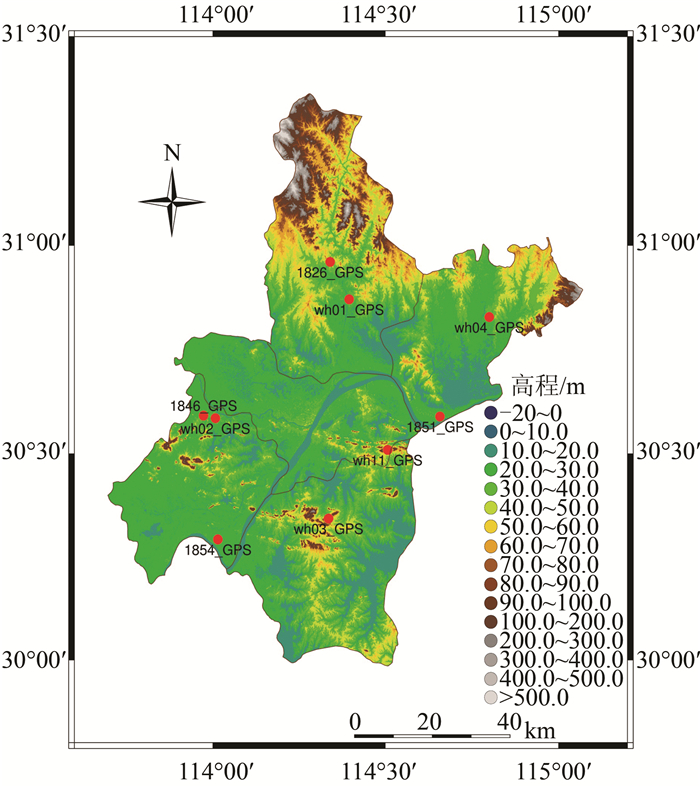 |
| 图 1 武汉市高程及CGCS2000点位分布图 Fig.1 Wuhan Topographic Map and CGCS2000 Points Distribution |
从图 1中可以看出,武汉市总体地形较为平坦,北部为山地,地形起伏较大,在投影面选取的时候尽量考虑地势平坦地区的投影变形,山区可以适当放宽投影变形的要求。图 1给出了武汉地区的CGCS2000控制点的分布情况,可以看出整个武汉地区只有9个CGCS2000控制点,数量少,且分布不均匀,这些点1826_GPS、1846_GPS、1851_GPS、1854_GPS、wh01_GPS、wh02_GPS、wh03_GPS、wh04_GPS和wh11_GPS的高程依次为:34.764 581 m、18.390 29 m、10.547 1 m、9.916 422 m、20.549 95 m、25.101 58 m、66.956 15 m、17.036 92 m和68.419 63 m,其平均高程为30.18 m。
投影面高度从0 m开始,每隔10 m,根据式(9)分别计算不同投影高程面下的投影变形,利用GMT软件绘制投影变形分布图,并计算其RMS值,结果如图 2所示。
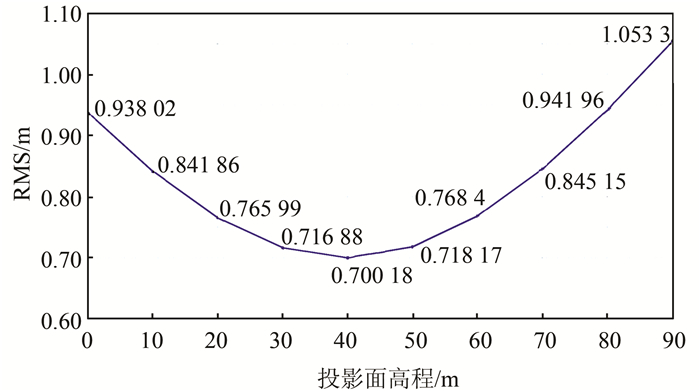 |
| 图 2 武汉市不同高度投影面的RMS值 Fig.2 RMS of Projection Planes with Different Height |
从图 2中可以看出,当投影面高度为40 m时,其RMS值最小,即投影变形最小。由于篇幅限制,本文只给出投影面为40 m时的投影变形分布图,如图 3所示。从图 3中可以看出,武汉市除了北部的山区外,其余地区的投影变形都在2.5 cm/km之内,可以选择40 m为投影高程面。
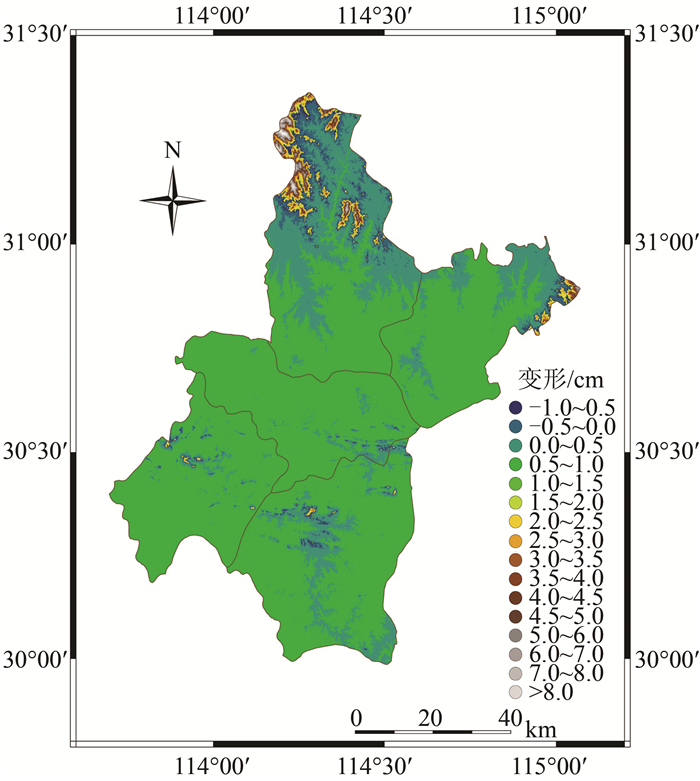 |
| 图 3 投影面为40 m时武汉地区的投影变形分布图 Fig.3 Projection Deformation at 40 m Projection Plane |
在确定出最佳投影面之后(图 3),与武汉地区的CGCS2000控制点的平均高程作比较,如果按照传统方法选择这些点的平均高程30.18 m作为投影面,其与本文方法选择的投影面之间存在着大约10 m的差距,这主要是由于CGCS2000点分布不均匀,点位稀疏造成的。从图 2中的RMS值可知,投影面高程为30 m时,RMS值为0.716 88 m;投影面高程为40 m时,RMS值为0.700 18 m。两者的RMS值相差不大,实际工作中这两个投影面都可以选择,证明了本文方法的可行性,并且本文方法克服了传统方法点位不足的缺点,实现了投影面选取的可视化,有利于结合实际的地形条件选取合适的投影面。
3 结束语在利用传统方法选取投影面时,无法充分考虑整个测区的地形条件,继而无法选择出与整个测区地形符合最好的投影面。特别是在高海拔、地形起伏较大的地区,作业困难,控制点更加稀少,而本文提出的方法可弥补传统方法的不足,利用3″×3″分辨率的SRTM地形数据,每隔90 m可以选取一个格网点,格网点分布均匀,能够更好地估计地形条件选取投影面。另外,利用GMT软件可以将测区地形图和投影变形分布图直观地呈现出来,实现了投影面选取的可视化,有利于结合实际的地形条件及经济发展需要选取合适的投影面。
| [1] |
李文华, 李寻. 高原地方坐标系的理论设计与投影变形检验[J]. 测绘科学, 2015, 40(10): 79-83. |
| [2] |
黄德伦.基于CGCS2000的地方独立坐标系模型构建及实例分析[D].西安: 西安科技大学, 2013 http://d.wanfangdata.com.cn/Thesis_D347504.aspx
|
| [3] |
李江卫, 白洁, 郭际明, 等. 基于CGCS2000的城市平面坐标系最佳选取[J]. 测绘科学, 2011, 36(4): 63-65. |
| [4] |
耿晓燕.地方独立坐标系向2000国家大地坐标系转换研究[D].西安: 西安科技大学, 2010 http://cdmd.cnki.com.cn/Article/CDMD-10704-2011014897.htm
|
| [5] |
杨志, 覃辉, 文鸿雁, 等. 基于投影变形大小的投影带和投影面选择[J]. 公路工程, 2016, 41(1): 59-63. DOI:10.3969/j.issn.1674-0610.2016.01.013 |
| [6] |
王淑玲, 刘振宇, 高炳浩. 利用最优化方法确定最佳城市独立坐标系[J]. 测绘科学技术学报, 2013, 30(6): 569-571. DOI:10.3969/j.issn.1673-6338.2013.06.005 |
| [7] |
范一中, 王继刚, 赵丽华. 抵偿投影面的最佳选取问题[J]. 测绘通报, 2000(2): 21-22. |
| [8] |
王继刚, 王坚, 于先文. 具有抵偿面的任意带高斯投影直角坐标系的选取方法[J]. 测绘通报, 2002(11): 31-32. DOI:10.3969/j.issn.0494-0911.2002.11.011 |
| [9] |
党亚民, 成英燕, 薛树强. 大地坐标系统及其应用[M]. 北京: 测绘出版社, 2010.
|
| [10] |
林华健. 基于最小二乘的具有高程抵偿面的任意带高斯投影变换方法研究[J]. 测绘地理信息, 2017, 42(3): 34-36. |
| [11] |
尹伟言, 赵鑫. 不同独立坐标系的比较以及最佳选取问题[J]. 测绘地理信息, 2017, 42(3): 18-21. |
 2019, Vol. 44
2019, Vol. 44

