| 一种基于熵权法理论的水准网平差定权方法 |
2. 云南坤测科技有限公司,云南 昆明,650100
2. Yunnan Kunce Survey Technology Co., Ltd., Kunming 650100, China
就大地测量学而言,有效获取高精度高程的方法仍然是几何水准测量。近年来,水准测量的精度随着现代测量中数据处理技术的发展也取得了显著性的提高。对水准网数据的处理方法通常是采用间接平差法,在平差中就会涉及到高差定权问题,针对定权问题一般采用两种方式,其一为按照距离千米数定权,另一种为按照测段内的测站数定权[1]。此两种方法应用很广,但是,对于地形复杂的区域,特别是起伏情况普遍地区,这两种方法都很难有效地反映水准测量的真实精度[2, 3]。基于此,本研究提出一种综合的定权方法,基于熵权理论,充分考虑测段内距离千米数和测站数中所包含的信息,并综合拟定它们的权重,进而得到一种具有综合信息的定权方法,该方法能有效整合上述两种常用定权方法的优点,进而可以充分适应复杂地区的定权问题。最后,本研究将建立的新的定权方法与常用的方法进行了对比分析,并采用单因素方差分析对最后的结果进行分析,从而验证本文提出方法和常用方法在精度上具有显著的优越性。
1 熵权法理论在水准网平差处理中,涉及定权问题,正如前面所述,常用的两类定权方法都比较适用于特定的地形,一种适用于平缓地区,一种适用于地形起伏较为显著的地区。可见,测段内的距离千米数和测站数都含有丰富的高差定权信息。因此,为综合利用测段内的距离千米数和测站数中携带的定权信息,本文采用熵权法拟定距离千米数和测站数在高差定权中所占权重,得到对应的权重向量。熵权法是一种客观赋权的方法,可避免人为主观因素的影响,其来源于信息论,“熵”表征的是系统的紊乱程度[4],若某评价指标的熵值越小,则反映该指标包含的信息量越大,即赋予较大的权重系数;反之,则赋予较小的权重系数[5, 6]。
将距离千米数和测站数视为两个影响因子,设第j个影响因子为yj,为规避各影响因子的量纲对定权结果带来的影响,对原始数据做归一化预处理:
| $ {x_{ij}} = 0.1 + \frac{{0.9\left( {{y_{ij}} - \min \left( {{y_{ij}}} \right)} \right)}}{{{{\max }_j}\left( {{y_{ij}}} \right) - {{\min }_j}\left( {{y_{ij}}} \right)}} $ | (1) |
式中,xij为归一化值;maxj(yij)为第j个影响因子的最大值;minj(yij)为第j个影响因子的最小值。
然后,根据信息熵的定义,计算各影响因子的信息熵:
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{ij}} = \frac{{{x_{ij}}}}{{\sum\limits_{i = 1}^m {{x_{ij}}} }}}\\ {{H_j} = - \frac{1}{{\ln m}}\sum\limits_{i = 1}^m {{P_{ij}}} \ln {P_{ij}}} \end{array}} \right. $ | (2) |
式中,Pij为待求的第j个影响因子向量中第i个值所占该影响因子的概率;Hj为第j个影响因子的信息熵;m为评价对象的数目;n为影响因子的数目。
最后,可通过计算得到的所有影响因子信息熵进一步计算各影响因子的熵权:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _j} = \left( {1 - {H_j}} \right)/\sum\limits_{j = 1}^n {\left( {1 - {H_j}} \right)} }\\ {\sum\limits_{j = 1}^n {{\omega _j}} = 1;j = 1, 2, 3, \cdots , n}\\ {{\omega _j} \in [0, 1]} \end{array}} \right. $ | (3) |
式中,ωj为第j个影响因子的权重系数。
通过式(3)可以计算出距离千米数和测站数权系数向量w = (ω1,ω2)。最后将w与式(2)中的Pij相乘,便得到第i个观测值的权重,记为wi,即得到了基于熵权法的定权结果。此后,可以顺利地运用加权最小二乘法进行水准网平差运算。
2 常用的水准网定权与平差方法水准测量结束后需要对数据进行处理,数据处理一般需要经过3个阶段,首先是需要对水准网高差观测值进行定权计算,通常采用两种常用的方法完成该部分工作,即按照测段内的水准路线长度定权或者按照测段内的测站数定权[7]。其次,需要求解每一个测段内的高差改正量,多采用间接平差法完成该项工作,得到各个水准点上的高程平差值[8, 9]。最后,完成验后精度评定,评定时依据验后单位权中误差。
当进行水准网平差操作时,会涉及到多条水准路线,可将每一条水准路线的观测视为被评价的对象,评价指标自然是影响该线路观测值的各种影响因素[10-13]。假如涉及到m条路线问题,每条路线都有n个影响因子,原始数据矩阵X可由观测数据、距离千米数以及测站数构成,随后利用上述提及的熵权理论求解距离千米数和测站数权重矩阵[14-16],即观测值定权结果。本文提出的基于熵权法理论的水准网平差定权流程如图 1所示。在观测值的权重分配后,按照间接平差原理计算完成后续操作。
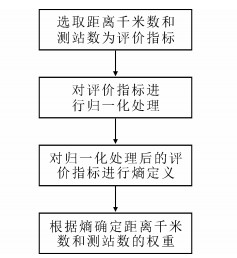 |
| 图 1 熵权法定权流程 Fig.1 Entropy Weight Process |
3 算例分析
选用某一地形复杂区域的水准网数据作为实例(见图 2),分别按照每个测段内的距离千米数、测站数以及本文提出的熵权理论定权,而后分别进行平差计算,最后对比分析不同定权方法下的水准网平差结果以评价定权方法的可靠性,也即是它们对水准网平差结果的效果。此外,基于水准网平差结果,采用置信水平为0. 05的单因素方差分析对3种不同的定权方法效果做统计性的分析以判断本研究所提方法的可靠性和合理性。图 1中A点为已知高程的水准点,表 1为水准网的测量结果,目的是为了求得未知高程的水准点B、C、D的高程数据。可依据水准测量数据通过间接平差技术求解水准点B、C、D的高程平差值。
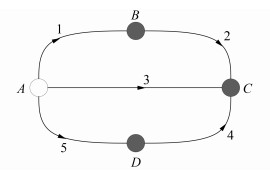 |
| 图 2 水准网示意图 Fig.2 Schematic Diagram of Leveling Network |
| 表 1 水准网观测数据 Tab.1 Level Net Observation Data |
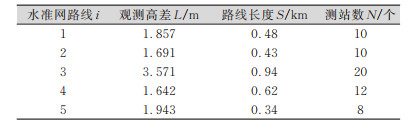 |
根据上述的熵权理论定权方案依据表 1中的数据求得定权结果,此外,为作对比分析,同时采用常用的两种定权方法进行定权计算,即分别只利用测段内的距离千米数信息和测站数信息建立两种定权方法并完成定权计算,得到水准网观测值的定权结果,如表 2所示,分别为上述3种定权方法的定权结果。
| 表 2 水准网观测数据定权结果 Tab.2 Weighted Results of Observation Data from Leveling Network |
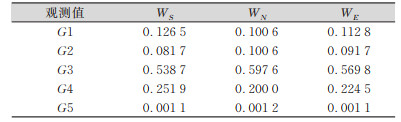 |
通过表 2中的数据可见,3种定权方法下求取的权重数据具有一定的差异,客观上也说明了在对水准网做平差处理时,不同的定权方法选取确实是会对整个平差结果产生一定的影响,也再次揭示了水准网的测量平差中选取可靠的定权方法的重要性。
在表 2中权重数据的基础上,利用间接平差计算方法求取平差数据,计算公式为:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} - \mathit{\boldsymbol{l}} $ | (4) |
式中,P为含有定权偏差的水准测量权矩阵;N为测段法方程系数矩阵;V为测段高差改正数;l为误差方程常数项;B为由水准网图形构成所决定的系数矩阵。经过计算可以得到各个定权方法下的平差数据,如表 3所示。
| 表 3 水准网待定点高程平差精度评定结果/mm Tab.3 Leveling Network to be Fixed Point Adjustment Accuracy Evaluation Results/mm |
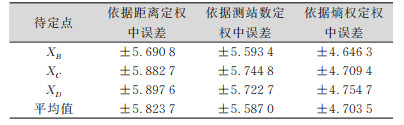 |
对水准网待定点高程平差精度评定结果进行统计性描述(见表 4),由表 4中的结果可见,本研究体提出的基于熵权理论进行定权的中误差的平均值最小,为±4. 703 5 mm,另外利用两种常用的定权方法进行定权的中误差平均值相差甚微,分别为±5. 823 7 mm和±5. 687 0 mm,均大于本文提出的定权方法下的中误差平均值。
| 表 4 水准网待定点高程平差精度评定结果描述 Tab.4 Description of the Adjustment Accuracy Evaluation Results of the Leveling Network to be Fixed Point |
 |
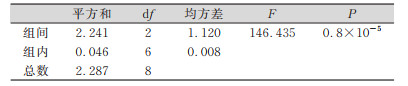
为了进一步分析讨论本文提出的熵权理论定权结果对水准网平差处理的有效性和合理性,对上述水准网的待定点高程平差精度的评定结果做单因素方差分析(在0. 05的置信水平下),表 5为分析结果,从表 5中可以看出,P=0.8×10-5 < 0. 05,说明本研究提出的定权方法应用效果与另外两种常用方法应用效果之间的差异具有统计学意义,也即说明本研究提出的熵权理论定权法的应用效果显著优于常规定权方法,相对于常用的两种定权方法而言,本文提出的方法更为合理,且得到的最终水准网平差值的精度更高,更适用于复杂地形区域的测量平差。
| 表 5 水准网待定点高程平差精度评价结果的单因素方差分析 Tab.5 Single Factor Analysis of Variance(Anova)of AdjustmentAccuracy Evaluation Results for Fixed Point in Leveling Network |
 |
4 结束语
针对水准网的测量平差中存在的定权问题,本文在充分了解常用的两种定权方法后,发现其在定权时都具有片面性,对于复杂起伏条件下的水准网测量数据的处理仍然存在缺陷,基于此,本研究在这两种定权方法的基础上提出了一种充分整合测段内的距离千米数和测站数中所带的定权信息的新的定权方法,即通过利用信息熵理论背景下的熵权法,综合考虑测段内的距离千米数和测站数信息而建立的熵权法定权方案。最后通过实例对比分析3种定权方法的应用效果,并采用统计学分析方法分析了结果的合理性和可靠性。
1)在水准网平差时的观测高差定权问题中,常用的两种定权方法应用受测区地形的约束性较大,因为它们对于不同的地形条件都不具有普适性,都只能适用于部分地形条件,如地形起伏不太显著的区域或者地形起伏较为明显的区域,然而,对于地形相对复杂的测区,因为同时存在多种不同起伏情况的测段致使单选用两种常用的定权方法中的一种都不能有效反映出水准测量的实际精度。
2)为解决常规定权方法存在的缺陷,即不能很好地适用于同时存在多种不同类型的地形条件的测段,本研究提出一种基于熵权理论的观测值定权方法。采用3种不同的定权方法某一地形复杂区域的水准网做平差处理,对比3者的高程平差精度评定结果可见,本文提出的新的定权方法具有较大优势,最终平差值的平均精度相对更高。
3)最后为了进一步分析讨论本文提出的熵权理论定权结果对水准网平差处理的有效性和合理性,对上述水准网的待定点高程平差精度的评定结果做单因素方差分析,结果表明研究提出的定权方法应用效果与另外两种常用方法应用效果之间的差异具有统计学意义,即说明本研究提出的熵权理论定权法的应用效果显著优于常规定权方法。本方法提出的新的定权方法普适性更强,尤其是针对测区地形复杂条件下的水准测量数据处理问题,可在一定程度上提高水准测量中平差结果的可靠性,是一种良好的水准网平差定权方法,具有一定的推广价值。
| [1] |
姜佃高, 邢鹏飞. 水准网平差中常用抗差估计方法的有效性研究[J]. 北京测绘, 2017(5): 6-10. |
| [2] |
赵言, 花向红, 尹志永. 基于定权的多因子线性拟合方法研究[J]. 测绘工程, 2012, 21(4): 5-8. DOI:10.3969/j.issn.1006-7949.2012.04.002 |
| [3] |
谢建, 朱建军. 不等式约束秩亏网平差的算法研究[J]. 大地测量与地球动力学, 2011, 31(6): 117-120. |
| [4] |
常文倩, 唐德善, 唐肖阳, 等. 河长制下黄沙港河道岸线资源开发利用评价[J]. 水电能源科学, 2018, 36(12): 83-86. |
| [5] |
张顺堂, 吴昌友. 基于熵权可变模糊评价模型的矿井火灾安全性评价[J]. 数学的实践与认识, 2018, 48(23): 175-182. |
| [6] |
王攀. 高煤阶煤储层非均质性耦合模型及煤层内含气量影响因素权重分析[J]. 煤炭技术, 2018, 37(1): 51-54. |
| [7] |
王磊, 郭际明, 喻永平, 等. 水准网定权方法对精度评定的影响[J]. 测绘通报, 2011(5): 26-28. |
| [8] |
Kang Q, Fan Q W, Zurada J M. Deterministic Convergence Analysis via Smoothing Group Lasso Regularization and Adaptive Momentum for Sigma-Pi-Sigma Neural Network[J]. Information Sciences, 2021, 553: 66-82. DOI:10.1016/j.ins.2020.12.014 |
| [9] |
Fan Q W, Kang Q, Zurada J M. Convergence Analysis for Sigma-Pi-Sigma Neural Network Based on some Relaxed Conditions[J]. Information Sciences, 2022, 585: 70-88. DOI:10.1016/j.ins.2021.11.044 |
| [10] |
郭际明, 杨学彬, 陈劲林. 引水隧洞洞内平面控制网布设方案设计与分析[J]. 测绘地理信息, 2017, 42(2): 17-20. |
| [11] |
郭际明, 邬应忠, 赵建双. 多级导线网的统一平差研究[J]. 测绘信息与工程, 2001, 26(3): 9-12. |
| [12] |
曹强, 郇英程, 陈民坤. 中间设站法三角高程测量代替三等水准测量探讨[J]. 北京测绘, 2018, 32(9): 1 034-1 036. |
| [13] |
聂建亮, 刘晓云, 田婕, 等. 利用自适应水准网动态平差建立山东垂直运动速度模型[J]. 武汉大学学报·信息科学版, 2020, 45(4): 620-625. |
| [14] |
付新启. 论测量平差中必要观测数的确定[J]. 北京测绘, 2018, 32(1): 40-43. |
| [15] |
王永弟, 许承权. 熵权理论在测量平差中的应用[J]. 测绘通报, 2012(11): 52-54. |
| [16] |
陈振国, 唐龙江. 基于稳健总体最小二乘的GPS水准拟合研究[J]. 测绘地理信息, 2018, 43(4): 84-87. |
 2022, Vol. 47
2022, Vol. 47


