| 城市土地密度圈层分布的反S型规律及其应用 |
2. 武汉大学地理信息系统教育部重点实验室,湖北 武汉, 430079;
3. 地球空间信息技术协同创新中心,湖北 武汉, 430079
2. Key Laboratory of Geographic Information System, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
城市土地是人类聚集活动的场所,城市土地的增长是重要的地理空间动态演化过程。许多研究利用城市景观指标对城市土地形态进行表征[1-3],这些研究主要集中在斑块尺度和景观尺度[4, 5]。对城市中人口密度分布的研究发现城市活动呈同心分布,即经济活动的密度随着距离的增加而逐渐衰减。文献[6]通过对城市内部人口密度分布的研究建立了几个经典模型来描述其随中心到边缘距离的变化;Clark[7]使用指数模型来衡量城市人口密度从中心向边缘地区下降的规律;Berry等[8]提出随着城市中心距离的增加城市人口密度以负指数方式下降; Batty等[9]则将逆幂模型和负指数进行比较并基于实证研究指出逆幂模型更适用于城市人口密度分布。但对衡量城市土地密度分布的研究较少。笔者将城市土地密度定义为城市地区不透水表面占比,探究城市土地密度分布规律。在前期研究中,笔者发现城市土地密度分布呈现反S型分布规律,并提出了反S函数来定量分析城市土地密度分布规律[10]。
在研究国内主要城市土地密度分布特征的基础上,选取9个美国、13个欧洲人口总量大于100万的典型城市,来获取1990年、2000年和2014年城市土地利用数据,从而进一步分析城市土地密度分布变化规律。对单中心、多中心城市分别进行定量拟合分析,根据城市土地密度分布特征,将城市划分为核心区、内城区、郊区和边缘4个区域,利用反S函数拟合参数定量分析城市扩张特征并比较城市形态变化过程。进一步地,以武汉市为例,根据城市的不同方向、交通廊道分析城市土地密度的反S型分布及分区异质性;利用商业网点密度、人口密度、容积率、道路密度等城市地理要素数据,以分析验证不同地理要素的反S型集聚特征。
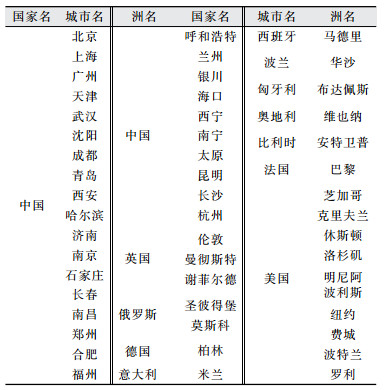
1 数据与方法 1.1 数据获取及信息提取中国样本城市的研究时期为1990年、2000年和2010年,其具体信息如表 1所示。遥感影像数据来源于美国地质调查局(United States Geological Survey,USGS)官方网站开源数据,选取的是美国陆地卫星(Landsat)的TM(thematic mapper)/ETM+(enhanced thematic mapper plus)影像。遥感数据处理包括影响几何校正、图像拼接、图像融合、图像裁剪和影像增强。结合目视解译和监督分类,将遥感影像数据分为不透水表面、水体、绿地和其他用地4类,再提取各城市的不透水表面数据,各期遥感影像总体分类精度在85%~93%。美国和欧洲城市信息如表 1所示,城市土地利用数据来源于Atlas of Urban Expansion:the 2016 Edition[11],数据集中遥感影像时间约为1990年、2000年和2014年,城市用地分为建成区、开放空间(植被等)和水域3类。笔者选择数据中的建成区作为城市不透水表面数据。
| 表 1 研究城市所在地区信息 Tab.1 Regional Information of Sample Cities |
 |
1.2 城市土地密度计算
采用圈层梯度分析对城市进行圈层划分。圈层分析是以城市中心为圆心向外做一系列等距的缓冲区,将其作为刻画城市扩展空间分异的基本单元,用以计算相关空间指标[12]。在圈层法缓冲分析中,选择一个缓冲环作为城市的最终边界,这个边界应该足够大,包括空间连续、构成一体化城市功能的城市区域和城市的外环路;同时应排除远离主城区的独立小城市。
根据城市主要用地结构和功能布局,将城市分为单中心和多中心城市两种主要的类型。根据城市的圈层划分,各缓冲带内的城市土地密度为不透水表面的面积与可利用土地的面积之比(可利用土地面积不包括河流、大型湖泊等不可建设或受保护区域的面积)。
1.2.1 单中心城市单中心城市中心功能强大,具有集中资源和影响整个城市的作用,中心往往位于城市中央位置或城市起源地及其附近,具有明显的交通优势。对单中心城市进行圈层划分,即以各城市中心为圆心,建立一系列宽度为1 km的缓冲带。单中心城市以北京、芝加哥和柏林为例(图 1)。北京市处于华北平原地区,是典型的平原城市,城市建设用地呈片状分布,以天安门为圆心向外呈圈层扩张; 芝加哥位于美国中西部,东邻密歇根湖,为典型的单中心城市,城市形态呈“手掌状”由中心区卢普区向北、西、南3个方向发展; 柏林为城市范围较小的单中心城市,以城市中心区向外呈圆环状发散发展。
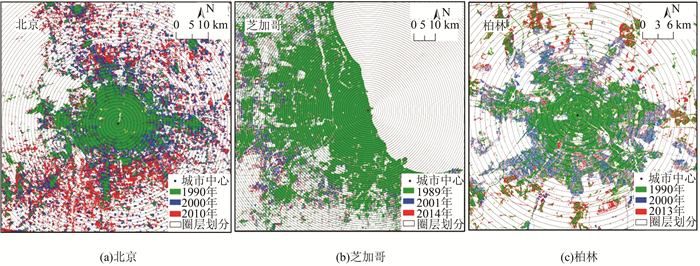 |
| 图 1 单中心城市北京、芝加哥和柏林圈层梯度分析 Fig.1 Buffer Analysis of Beijing, Chicago and Berlin |
1.2.2 多中心城市
多中心城市中往往存在多个中心,如市区均衡多中心型(城市内部分布多个功能相当的城市中心)、非均衡多中心型(除了城市主中心外存在其他次级的副中心)和带状多中心型(由于地形地貌限制城市带状发展)。多中心城市以武汉、杭州和兰州为例(图 2)。武汉为均衡多中心城市,由长江、汉江等水系的阻隔作用形成汉阳、汉口和武昌3区多中心组团的格局,3个城市核心区中心功能强大、集聚程度强且相互之间作用力较为均衡。因此以武昌、汉阳和汉口的3个商业中心为城市中心; 杭州为非均衡多中心城市,杭州1990年和2000年以单中心城市发展,2010年时已发展为多中心城市,确定2010年杭州市主中心及次中心位置,以主、副中心连线为轴线建立1 km宽度带,计算各缓冲带内土地密度,以最低土地密度带为主、副中心作用力边界; 兰州市是典型的带状多中心城市,主城区布局在地形封闭的河谷盆地中,由于受到河谷地形及其周围山地的限制,向外围发展困难,随着城市规模的不断扩大,城市被迫沿着河流走向带状发展。
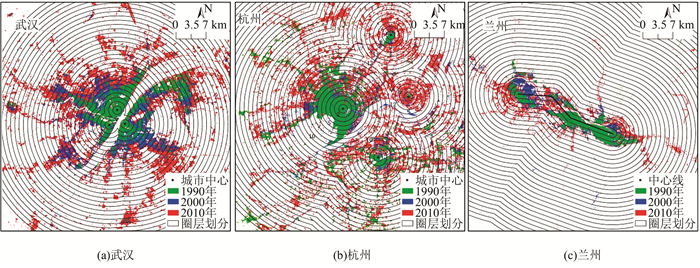 |
| 图 2 多中心城市武汉、杭州和兰州圈层梯度分析 Fig.2 Buffer Analysis of Wuhan, Hangzhou and Lanzhou |
1.3 城市土地密度分布特征及反S函数
典型城市土地密度变化散点图如图 3所示,图中城市土地密度随城市中心距离增加而逐渐减少。城市土地密度在靠近城市中心区密度高,随距离增加先缓慢减小,然后快速减小,最终在城市边缘区维持一定的密度。
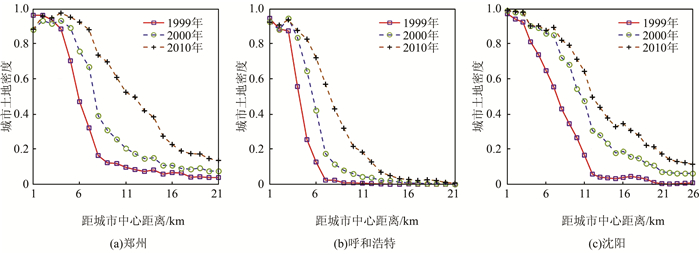 |
| 图 3 城市土地密度从中心向外递减分布特征 Fig.3 Urban Land Density Measured from Urban Centers |
在研究中国28个重要城市土地密度分布随城市中心向外递减的规律时,笔者发现城市土地密度分布随城市中心向外降低呈反S型规律[10],并据此提出了城市土地密度分布反S函数。城市土地密度反S函数公式为:
| $ f\left( r \right) = \frac{{1 - c}}{{1 + {{\rm{e}}^{\alpha \left( {\frac{{2r}}{D} - 1} \right)}}}} + c $ | (1) |
式中,f为城市土地密度;r为离城市中心的距离;e为自然常数;α、c和D为拟合参数,α为控制城市密度方程曲线斜率的参数,c为城市边界附近土地密度,D为对城市主城区半径的估计结果。土地密度函数曲线分布及空间结构划分如图 4所示。图 4中r0表示土地密度曲线下降最快的地区,而r1和r2分别表示城市土地密度函数曲线下降的拐点,以此将城市划分为核心区、内城区、郊区和边缘区[10]。
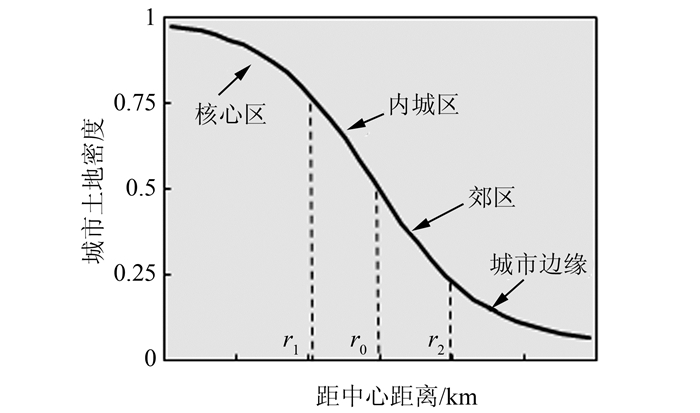 |
| 图 4 城市土地密度分布空间结构划分 Fig.4 Graphs of the Divided Urban Structure of Urban Land Density Function |
2 城市土地密度分布的反S函数拟合结果
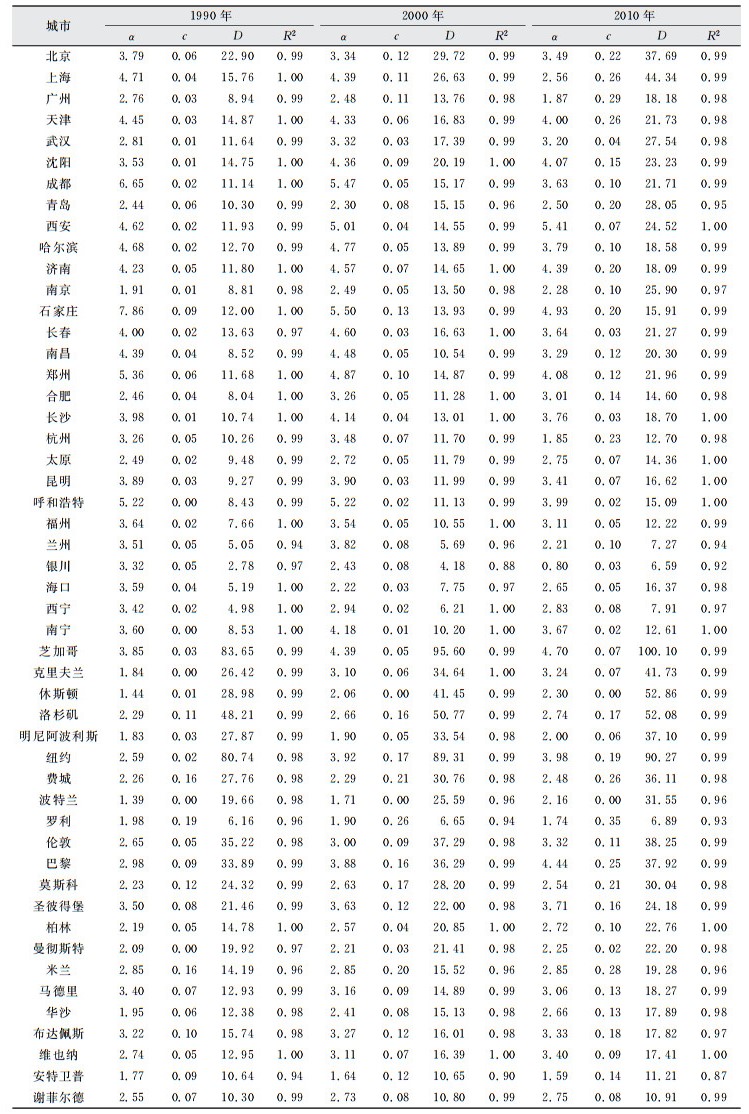
中国、美国、欧洲城市土地密度分布反S函数拟合参数结果如表 2所示。典型城市土地密度分布拟合曲线如图 5所示。所有的拟合效果R2均在0.88以上,其中95%以上的R2>0.95。
| 表 2 中国、美国、欧洲城市土地密度反S函数拟合参数 Tab.2 Parameters of the Fitted Urban Density Functions of Cities in China、America and Europe |
 |
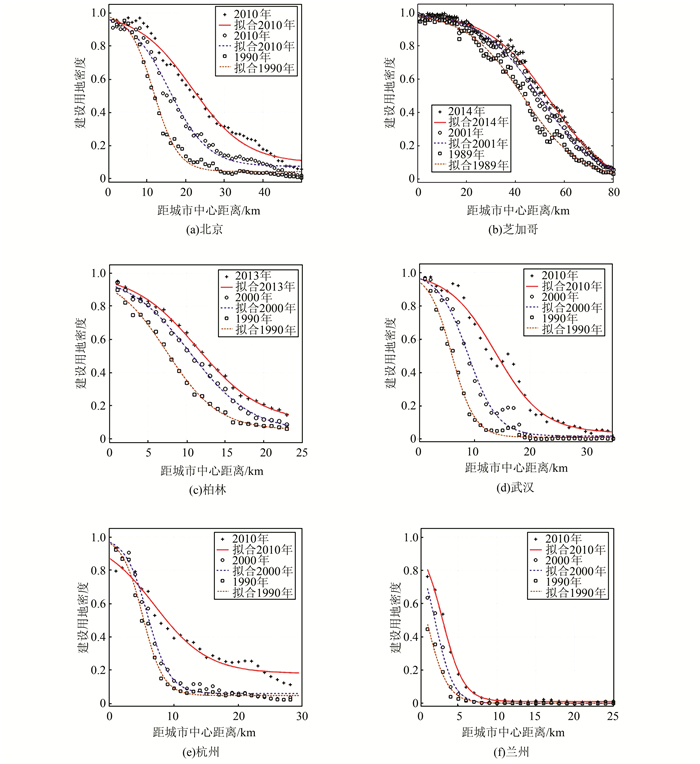 |
| 图 5 典型城市土地密度反S函数拟合曲线 Fig.5 Graphs of the Fitted Urban Land Density Functions of Typical Cities |
3 城市土地密度分布反S规律应用 3.1 城市形态分析
城市土地密度呈反S型分布,并且分布形式可以用反S函数定量描述。在前期研究中,笔者根据城市土地密度分布曲线下降速度,将城市划分为核心区、内城区、郊区和边缘区[10],并且使用城市土地密度曲线中快速下降的部分所占的比例用来衡量城市形态的紧凑程度(Kp)[10]。紧凑城市的土地密度从城市中心下降到边缘区的速度快,Kp值较小;而蔓延的城市土地密度从城市中心下降到边缘区的速度较慢,Kp值较大。Kp表示内城区与郊区的占比,其计算公式如下:
| $ {K_p} = \frac{{r2 - r1}}{D} = \frac{{1.316957}}{\alpha } $ | (2) |
中国、美国和欧洲城市3个时期Kp值的计算结果如图 6所示。平均来看,中国城市空间形态最为紧凑,但在过去20 a城市发展中,城市紧凑度降低,变得更加蔓延;美国城市形态最蔓延,但是在过去20 a中,城市紧凑度增加,更为紧凑;欧洲城市较为紧凑,且在过去20 a紧凑度在增加,城市更为紧凑。
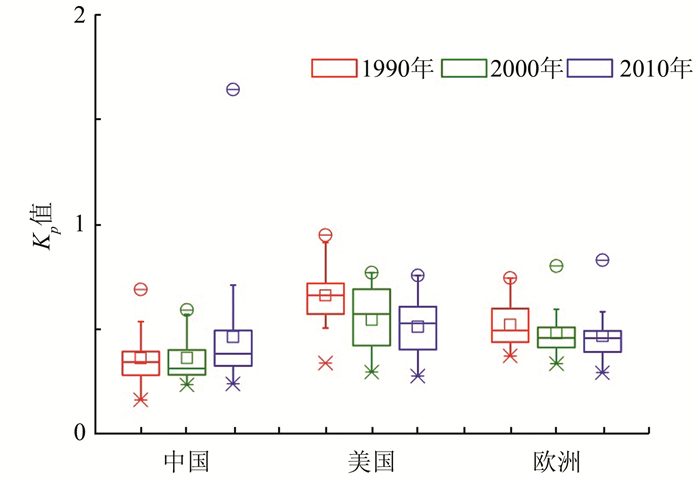 |
| 图 6 中国、美国和欧洲城市3个时期Kp值结果图 Fig.6 Kp of Cities in China, America and Europe of Three Time Points |
3.2 城市增长模式分析
城市土地密度在50%处表示城市主城区即核心区和内城区的范围[13, 14]。在Glaeser等[15]的研究中,利用城市发展范围靠近城市中央商务区(central business district,CBD)程度来表示城市中心度。据此,笔者计算中国、美国和欧洲城市在不同时期主城区半径范围的增长速度,来定量对比分析城市的增长速度,如图 7所示。从图 7中可以看出,美国城市主城区规模最大,欧洲城市次之,中国城市主城区最小;但是在过去20 a中,中国城市主城区规模增长率最高,美国城市次之,欧洲城市最低。中国城市虽然规模小,但发展速度最快;美国城市规模最大,发展速度中等;而欧洲城市发展速度最慢。
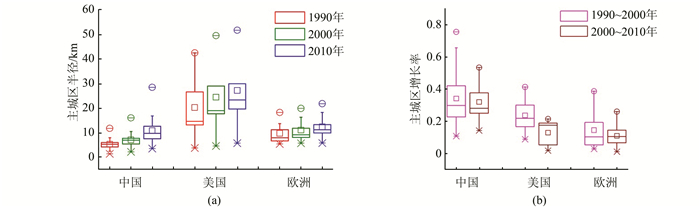 |
| 图 7 中国、美国和欧洲城市3个时期主城区半径增长率 Fig.7 Growth Rates of Radius of Urban Main Area of the Cities in China, America and Europe |
4 反S规律的推广 4.1 城市土地密度分布的空间异质性描述
城市廊道可以划分为自然廊道和人工廊道。自然廊道主要包括河流、植被带;人工廊道主要包括交通干线[16-18]。针对城市建设用地景观,交通廊道是城市空间扩展的伸展轴,对城市空间扩展具有引导作用[19-22],而自然廊道对其起阻隔作用。基于自然廊道(河流、湖泊)将武汉市划分为不同的扇形方向(图 8(a)),根据交通主干道选择6个主要的道路廊道(图 8(b))分别统计5个方向和6个廊道的城市土地密度,并利用反S函数进行拟合,如图 9所示。从图中可以看出,城市土地密度在不同方向分区、不同廊道分区上均呈现反S规律分布,但反S分布形态在不同方向具有异质性;交通廊道城市土地密度分布在不同廊道的异质性比扇形方向异质性更大。
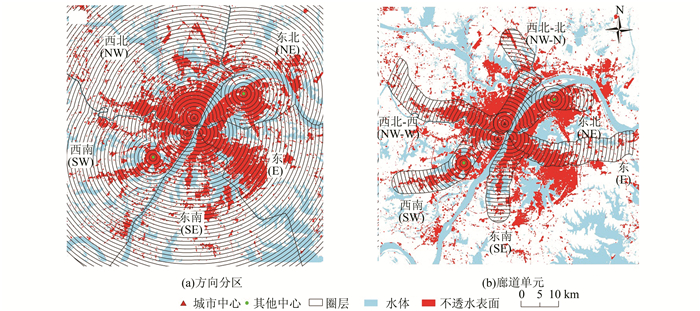 |
| 图 8 武汉不同方向、廊道分区分析单元 Fig.8 Analysis Units of Different Directions, Corridor Divisions in Wuhan |
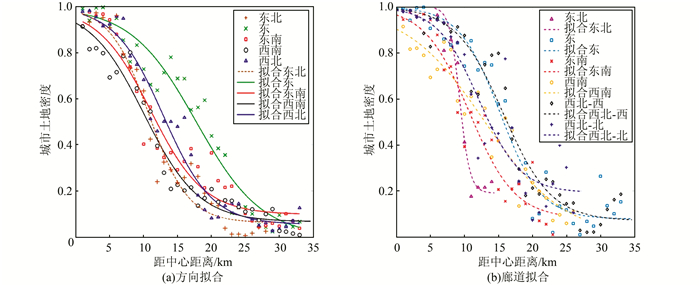 |
| 图 9 城市土地密度不同方向、廊道分区拟合 Fig.9 Fitting of District Units' Urban Land Density of Different Directions, Corridor Divisions |
4.2 城市地理要素密度分布的反S形态对比
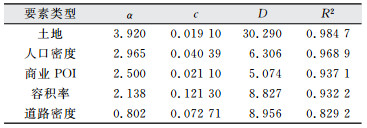
除了城市土地密度,其他地理要素分布也呈反S型规律。由于数据获取的限制,选取武汉市商业兴趣点(points of interest, POI)密度、人口密度、道路密度、容积率等城市地理要素,运用反S函数对其密度分布进行拟合分析(表 3、图 10)。拟合结果表明,这4类城市地理要素均呈现反S型分布,距离城市中心越远,城市地理要素的分布密度呈圈层递减分布。从图 10中可看出,商业POI密度、人口密度、容积率、道路密度所呈现的反S曲线形态存在差异。土地密度、道路密度的反S曲线最为平缓,道路密度下降较为缓慢,分布较为均匀;商业POI密度和人口密度分布曲线下降速度远快于其他要素,表明其向心集聚度最高。容积率和道路密度在距离城市中心不同距离出现明显的起伏,表明城市地理要素受到城市次中心、城市组团中心等的作用,城市次中心和城市组团中心的作用使得城市地理要素密度分布存在差异。
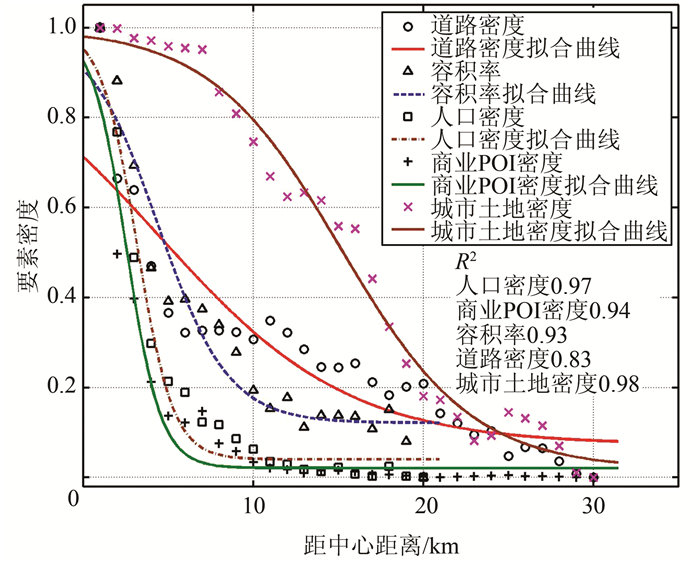 |
| 图 10 城市地理要素密度分布拟合 Fig.10 Fittings of Geographic Phenomena Densities for Foreign Cities |
| 表 3 城市土地要素密度反S函数拟合参数 Tab.3 Parameters of the Fitted Urban Density Functions |
 |
5 结束语
城市土地密度分布随距城市中心距离增加而逐渐降低的规律呈现反S型分布,并且此分布可以用函数定量描述,在此基础上可以对城市结构、增长速度和空间形态进行进一步分析。
1) 反S函数拟合国内外城市土地密度分布效果好、拟合优度高,且对于单中心城市、多中心城市的土地密度分布均适用,具有一定的普遍性。
2) 通过反S函数定量分析中国、美国和欧洲地区的城市土地密度分布,可以比较城市形态和扩张模式:中国城市空间形态最紧凑,但在过去20 a中,城市紧凑度降低,变得更加蔓延;美国城市形态最蔓延,但是在过去20 a中,城市紧凑度增加;欧州城市在过去20 a紧凑度在增加,城市更为紧凑。
3) 反S规律的推广应用。对武汉市分方向、分廊道土地密度分布进行分析发现,反S函数拟合优度高,可以分析城市扩张异质性;进一步地,武汉市商业POI密度、人口密度、容积率、道路密度等要素分布同样具有反S规律。这些研究表明反S规律在城市要素分布中的普遍适用性。
| [1] |
Herold M, Couclelis H, Clarke K C. The Role of Spatial Metrics in the Analysis and Modeling of Urban Land Use Change[J]. Computers, Environment and Urban Systems, 2005, 29(4): 369-399. DOI:10.1016/j.compenvurbsys.2003.12.001 |
| [2] |
Bhatta B, Saraswati S, Bandyopadhyay D. Urban Sprawl Measurement from Remote Sensing Data[J]. Applied Geography, 2010, 30(4): 731-740. DOI:10.1016/j.apgeog.2010.02.002 |
| [3] |
Wilson E H, Hurd J D, Civco D L, et al. Development of a Geospatial Model to Quantify, Describe and Map Urban Growth[J]. Remote Sensing of Environment, 2003, 86(3): 275-285. DOI:10.1016/S0034-4257(03)00074-9 |
| [4] |
Irwin E G, Bockstael N E. The Evolution of Urban Sprawl: Evidence of Spatial Heterogeneity and Increasing Land Fragmentation[J]. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104(52): 20 672-20 677. DOI:10.1073/pnas.0705527105 |
| [5] |
Seto K C, Fragkias M. Quantifying Spatiotemporal Patterns of Urban Land-Use Change in Four Cities of China with Time Series Landscape Metrics[J]. Landscape Ecdogy, 2005, 20(7): 871-888. DOI:10.1007/s10980-005-5238-8 |
| [6] |
Wolch J R, Byrne J, Newell J P. Urban Green Space, Public Health, and Environmental Justice: The Challenge of Making Cities'Just Green Enough'[J]. Landscape and Urban Planning, 2014, 125: 234-244. DOI:10.1016/j.landurbplan.2014.01.017 |
| [7] |
Clark C. Urban Population Densities[J]. Royal Statistical Society, 1951, 114(4): 490-496. DOI:10.2307/2981088 |
| [8] |
Berry B J L, Simmons J W, Tennant R J. Urban Population Densities: Structure and Change[J]. Geographical Review, 1963, 53(3): 389-405. DOI:10.2307/212588 |
| [9] |
Batty M, Kim K S. Form Follows Function:Reformulating Urban Population Density Functions[J]. Urban Studies, 1992, 29(7): 1043-1070. DOI:10.1080/00420989220081041 |
| [10] |
Jiao Limin. Urban Land Density Function: A New Method to Characterize Urban Expansion[J]. Landscape and Urban Planning, 2015, 139: 26-39. DOI:10.1016/j.landurbplan.2015.02.017 |
| [11] |
Angel S, Blei A M, Parent J, et al. Atlas of Urban Expansion: Areas and Densities (The 2016 Edition, Volume 1)[M]. New York: New York University Press, 2016.
|
| [12] |
李晓文, 方精云, 朴世龙. 上海及周边主要城镇城市用地扩展空间特征及其比较[J]. 地理研究, 2003, 22(6): 769-779. DOI:10.3321/j.issn:1000-0585.2003.06.012 |
| [13] |
Kuang Wenhui, Chi Wenfeng, Lu Dengsheng, et al. A comparative Analysis of Megacity Expansions in China and the U S: Patterns, Rates and Driving Forces[J]. Landscape and Urban Planning, 2014, 132: 121-135. DOI:10.1016/j.landurbplan.2014.08.015 |
| [14] |
Schneider A, Woodcock C E. Compact, Dispersed, Fragmented, Extensive? A Comparison of Urban Growth in Twenty-Five Global Cities Using Remotely Sensed Data, Pattern Metrics and Census Information[J]. Urban Studies, 2008, 45(3): 659-692. DOI:10.1177/0042098007087340 |
| [15] |
Glaeser E L, Kahn M E. Sprawl and Urban Growth[J]. Handbook of Regional & Urban Economic, 2003(4): 2481-2527. |
| [16] |
宗跃光. 城市景观生态规划中的廊道效应研究--以北京市区为例[J]. 生态学报, 1999, 19(2): 3-8. |
| [17] |
宋丹阳, 夏畅, 王海军. 基于空间句法的不同道路密度区内土地利用特征研究--以武汉市为例[J]. 测绘地理信息, 2018, 43(2): 43-47. |
| [18] |
何建华, 李纯. 顾及人口流动交互的城镇景观动态模拟[J]. 测绘地理信息, 2017, 42(4): 1-7. |
| [19] |
黄宁, 吝涛, 章伟婕, 等. 厦门市同安区不同扩展轴上的景观格局梯度分析与比较[J]. 地理科学进展, 2009, 28(5): 767-774. |
| [20] |
李时雨, 刘艳芳, 孔雪松, 等. 武汉市生态用地景观格局的时空演化特征分析[J]. 测绘地理信息, 2016, 41(3): 68-73. |
| [21] |
李飞雪, 李满春, 刘永学, 等. 建国以来南京城市扩展研究[J]. 自然资源学报, 2007, 22(4): 524-535. DOI:10.3321/j.issn:1000-3037.2007.04.004 |
| [22] |
杨荣南, 张雪莲. 城市空间扩展的动力机制与模式研究[J]. 地域研究与开发, 1997, 16(2): 2-5. |
 2018, Vol. 43
2018, Vol. 43

