| 基于点云三维坐标数据计算复杂物体体积 |
2. 西安科技大学测绘科学与技术学院, 陕西 西安, 710054
2. College of Geomatics, Xi'an University of Science and Technology, Xi'an 710054, Shaanxi, China
规则物体体积可以应用固定的体积公式计算得出, 但在工程实际中, 诸如文物修复、古建筑复原、精密零件加工等, 被测量对象往往是不规则的, 导致体积的计算没有现成可以套用的公式。为计算不规则物体体积, 王泉德提出了三角网格模型体积计算方法[1]; 郭九生等进行了多面体最小体积的包围盒生成算法研究[2]。在工程测量领域, 传统上一般采用全站仪或全球定位系统观测物体特征点计算物体体积[3-5], 因其测量数据十分有限使得体积计算结果误差较大。利用三维激光扫描仪扫描出的点云坐标重构被测对象的几何模型, 获取测量对象的三维数据[6-7], 克服了全站仪、GPS无法获取海量三维坐标的缺点。涂超文等用移动式激光自动测量系统计算了大型堆场体积[8]; 王解先等进行了利用格网法计算堆积物体积研究[9]; 陈展鹏等研究了特征值拟合近似法滑坡堆积体体积计算[10]; 刘震将逆向工程软件与三维激光扫描设备相结合让计算精度达到了96.92%[11]。
本文采用法向量有向体积法计算物体体积, 将处理后的点云三维坐标投影到XOY平面, 对离散点云进行三角形剖分后再还原到各三角形顶点的真实高程点生成单面倾斜五面体, 逐个计算出单一五面体的体积, 进而求出总体积。
1 法向量有向体积法计算原理首先将构成的空间不规则体以三角形为最小单位分别向XOY平面进行投影, 在XOY平面上利用海伦公式计算出投影三角形的面积, 在分别以投影点的Z坐标值的平均值作为高, 从而可以得出三菱柱的体积。如图 1, 在不规则四棱柱abcd-a1b1c1d1中, 先连接bd, 将面abcd分割为△abd和△cbd。分别向XOY平面进行投影, 得到△a0b0d0和△c0b0d0。假设顶点a的坐标为(X1, Y1, Z1), 顶点b的坐标为(X2, Y2, Z2), 顶点d的坐标为(X3, Y3, Z3), 顶点c的坐标为(x4, y4, z4)。可得出各投影点a0、b0、c0、d0的坐标值。先利用海伦公式计算出△a0b0d0和△c0b0d0的面积。以△a0b0d0面积计算为例, 先计算△a0b0d0的3个边长a0b0、a0d0、b0d0, 分别为:
| $ {p_1} = \sqrt {{{({Y_2}-{Y_1})}^2} + {{({X_2}-{X_1})}^2}} $ | (1) |
| $ {p_2} = \sqrt {{{({Y_3}-{Y_1})}^2} + {{({X_3}-{X_1})}^2}} $ | (2) |
| $ {p_3} = \sqrt {{{({Y_3}-{Y_2})}^2} + {{({X_3}-{X_2})}^2}} $ | (3) |
 |
| 图 1 不规则四棱柱abcd-a1b1c1d1投影图 Figure 1 Projection of Irregular Quadrangular abcd -a1b1c1d1 |
根据边长可计算△a0b0d0的周长为:
| $ p = \frac{1}{2}({p_1} + {p_2} + {p_3}) $ | (4) |
根据海伦公式计算得出△a0b0d0的面积为:
| $ {S_{\Delta {a_0}{b_0}{d_0}}} = p \times (p-{p_1}) \times (p-{p_2}) \times (p-{p_3}) $ | (5) |
同理, 可得出△c0b0d0的面积。
再取a、b、d三点高程坐标z的平均值:
| $ {{\bar z}_{abd}} = \frac{1}{3}({z_1} + {z_2} + {z_3}) $ | (6) |
则三棱柱abd-a0b0d0的体积为:
| $ {V_1} = {S_{\Delta {a_0}{b_0}{d_0}}} \times {{\bar z}_{abd}} $ | (7) |
同理, 三棱柱cbd- c0b0d0的体积为:
| $ {V_2} = {S_{\Delta {c_0}{b_0}{d_0}}} \times {{\bar z}_{cbd}} $ | (8) |
三棱柱a1b1d1-a0b0d0的体积为:
| $ {V_3} = {S_{\Delta {a_0}{b_0}{d_0}}} \times {{\bar z}_{{a_1}{b_1}{d_1}}} $ | (9) |
三棱柱c1b1d1-c0b0d0的体积为:
| $ {V_4} = {S_{\Delta {c_0}{b_0}{d_0}}} \times {{\bar z}_{{c_1}{b_1}{d_1}}} $ | (10) |
在四棱柱abcd-a1b1c1d1中确定一点p, 其向外发出的多个方向的法向量i定义其指向XOY平面上方为正, 下方为负。即平面的法向量在XOY平面下方的体积为负, 上方为正。
由此得出四棱柱abcd-a1b1c1d1的体积为:
| $ V = {V_1} + {V_2} + {V_3} + {V_4} $ | (11) |
在实际应用中, 如果出现物体投影至XOY平面时有凹陷(如山体的悬崖)或底部非平面(如悬在空中的物体)等特殊情况时, 可根据实际情况选择投影面(XOZ/YOZ), 计算点云中每个点到投影面的法线距离, 设置投影分辨率, 选择同一法线上取法线距离最短的点, 将这些点与投影面(XOZ/YOZ)构造成一个多面体即空洞部分体积, 按照本文方法计算并从总体积中扣除。
2 模拟球体模型的体积计算赋予球体的半径为1 000 m, 经度、纬度均取0°~90°, 形成1/4球体。逐个提取所生成三角形每个顶点的坐标值, 使用模拟的点云数据构造空间的Delaunay三角网。再将三角形分别投影至3个坐标平面, 计算出3个坐标平面的投影三角形面积, 从而得出空间三角形的面积。在得到空间三角形后, 将空间三角形投影至XOY平面, 分别求出3个顶点Z坐标的平均值作为要求三棱柱的高, 求出三棱柱的体积, 对所有三棱锥体积求和就得到了模型总体的体积。构造的模型如图 2所示。
 |
| 图 2 模拟球体立体模型 Figure 2 Three-dimensional Simulation Model of a Sphere |
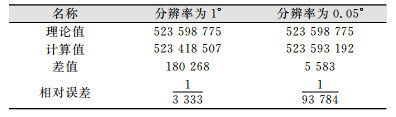
本文为比较不同分辨率和点云数据的全面性对体积计算的影响, 分别选取1°和0.05°两种经纬度模拟数据。其计算值与真实值的对比结果如表 1所示。
| 表 1 计算值与真实值对比结果/m2 Table 1 Comparison of Calculated and Actual Values/m2 |
 |
1) 构造三角网时对三角网的删减过程中可能导致某些区域不能连接成三角网, 从而影响了后续的计算结果。因此, 需要继续优化构建三角网的算法, 尽可能地减少此类误差。
2) 在提取三角形顶点坐标的过程中未能对有些三角形正确识别, 导致提取的坐标有可能重复, 从而在后续计算中导致误差。
3) 模拟球体数据的分辨率对体积计算精度影响较大, 分辨率为0.05°的计算结果明显优于分辨率为1°的计算结果, 但分辨率增加而产生的点位数据呈几何量级增长, 对计算机的硬件配置和计算速度要求极大, 在实际工作过程中必须依据工程项目对体积计算精度的要求而合理选择分辨率。
3 某假山模型的体积计算实验计算以某假山模型为测量对象, 通过扫描获取假山数据, 并对扫描所得的点云数据进行预处理, 构造出假山的三维模型。
3.1 点云坐标数据预处理三维激光扫描仪扫描得到的初始测量数据通常夹杂着大量的噪声点和其他的杂点, 在建立初始模型之前需要对点云数据进行数据的拼接、去噪以及精简等预处理, 以取得适用于建模要求的点云数据。
1) 点云数据拼接。通常情况下, 获取目标对象完整的三维点云数据必须进行多测站扫描, 但每次架设三维激光扫描仪都会建立一个独立的坐标系, 基于此, 必须将多测站点云数据转换到统一坐标系下形成三维点云数据。
2) 点云数据去噪。考虑三维激光扫描仪仪器本身的精度、被测目标的反射情况、测站的布设以及气温环境等影响, 需要对含有各类噪声的点云数据进行平滑处理。同时对扫描过程中因扫描盲区等从而造成数据缺失进行孔洞的修补、探寻孤立点并删除、消除噪声以及数据偏差纠正等。
3) 点云数据精简。依据工程所需精度选择合适计算模型分辨率, 对可视化表达的目标对象使用简化的模型对点云数据进行精简, 提高计算速度和效率。
3.2 建立三角网模型将三维空间坐标投影至XOY平面上, 利用X和Y坐标按照构网规则得到平面的不规则三角网, 之后赋予平面三角网Z值, 从而形成具有空间立体的三角网模型。对已经进行初步处理过的三维扫描数据进行模型的重新构建, 得到的假山模型如图 3所示。
 |
| 图 3 假山三角网模型 Figure 3 Rockery Triangular Mesh Model |
3.3 体积计算
在得到空间三角形后, 将空间三角形投影至XOY平面, 分别求出3个顶点Z坐标的平均值作为要求三棱柱的高, 求出三棱柱的体积, 对所有三棱锥体积求和就得到了模型总体的体积。利用点的源文件和三角形的顶点构成文件, 导入到体积计算程序, 得出假山的体积为28 537 861 915.420 6 m2。
4 结束语1) 通过对点云的模拟, 得出与理论值相近的结果, 并使得出的结果更加可控。
2) 实现了Delaunay三角网的构建, 对三角网构建算法改进的理论空间有了更加全面的认识。
3) 构造三角网时对三角网的删减过程中可能导致某些区域不能连接成三角网, 从而影响了后续的计算结果。解决的方法就是要继续优化构建三角网的算法, 尽可能地减少此类误差。构建三角网完成后, 需提取各个三角形顶点的坐标, 这里采用编程的方法, 算法计算量较大, 计算速度对计算机硬件要求较高, 在算法的优化上还有较大的改进空间。
| [1] |
王泉德. 任意三角格网模型体积的快速精确计算方法[J]. 计算机工程与应用, 2009, 45(18): 32-34. DOI:10.3778/j.issn.1002-8331.2009.18.009 |
| [2] |
郭九生, 初红艳, 卢秉恒. 多面体最小体积的包围盒生成算法研究[J]. 计算机应用, 2001, 21(1): 38-41. |
| [3] |
魏国武. 利用免棱镜全站仪进行采矿空间体积测量[J]. 有色矿冶, 2012, 28(1): 13-14. |
| [4] |
孔祥锋. 全站仪堆煤体积丈量法[J]. 山东煤炭科技, 2010(6): 112-114. |
| [5] |
向东, 汪志明, 赵建虎. RTK和TPS在矿料堆体积测量中的对比分析[J]. 城市勘测, 2002(1): 7-8. |
| [6] |
原玉磊, 骆亚波, 郑勇. 三维激光扫描仪在抛物面天线测量中的应用研究[J]. 测绘通报, 2012(2): 48-51. |
| [7] |
钱建国, 赵军武, 唐为刚, 等. 三维激光扫描仪获取的数据处理与应用研究[J]. 矿山测量, 2009, 37(6): 44-46. |
| [8] |
涂超文, 马斌. 移动式激光自动测量系统[J]. 测绘地理信息, 2013, 38(2): 69-70. |
| [9] |
王解先, 侯东亚, 段兵兵. 三维激光扫描仪在堆积物体积计算中的应用[J]. 测绘通报, 2013(7): 54-56. |
| [10] |
陈展鹏, 雷延武, 晏清红, 等. 汶川震区滑坡堆积体体积三维激光扫描仪测量与计算方法[J]. 农业工程学报, 2013, 29(8): 135-144. |
| [11] |
刘震. 逆向工程对不规则表面物体的体积测量[J]. 机电技术, 2009(3): 19-20. |
 2018, Vol. 43
2018, Vol. 43

