| 基于SVM的光学遥感影像分类与评价 |
快速、高精度的遥感影像自动分类算法是实现环境的动态监测、评价、预报的关键[1]。由于遥感影像的数据量大、数据维度高, 且不同地物的光谱特征和影像的分布特征千差万别, 使用传统的分类方法有较大的限制[2, 3], 因此, 探求适合于遥感影像的分类方法是遥感影像应用需要重点研究的课题。
目前, 遥感图像分类方法主要包括目视解译和计算机模式识别[4]。目视解译法质量受目视判读者的经验等因素制约; 计算机模式识别主要包括监督分类和非监督分类, 以数理统计学理论为基础, 一般在样本数目趋于无穷大时才能获得较好的分类精度, 但是实际工作中样本数目是有限的, 所以这些方法难以取得理想的分类效果。
Vapnik等在统计学习理论的基础上提出了支持向量机理论(support vector machine, SVM)。SVM算法是建立在统计学习理论的VC维理论和结构风险最小原理基础上, 根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷, 以期获得最好的推广能力[5-7]。通过解算最优化问题, 把特征向量从低维空间映射到高维空间, 在高维特征空间中寻找最优分类超平面, 从而解决复杂数据的分类问题[8-10]。
本文在研究SVM原理的基础上, 采用无人机遥感影像和Landsat 8 OLI/TIRS影像进行分类试验, 并利用总体精度和Kappa系数进行分类精度评价。结果显示, 该方法应用于光学遥感图像分类精度高, 是一种普适性较高的分类方法, 在光学遥感影像分类中有着广阔的应用前景。
1 SVM算法原理SVM是从线性可分情况下的最优分类超平面发展而来的[11], 如图 1所示[12, 13], 圆点和方点各代表一类样本, H为两类样本之间的分类线, H1和H2是各样本中距H最近且平行于H的直线, H1和H2之间的距离称为分类间隔, 最优分类超平面就是以最大分类间隔将两类样本正确分开的超平面[14]。
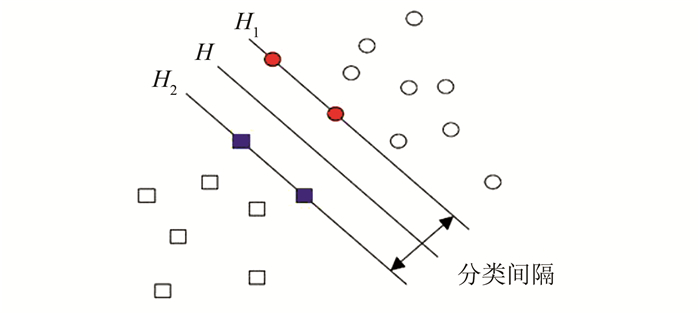 |
| 图 1 最优分类超平面 Fig.1 Optimal Classification Hyper Plane |
给定两类可分的训练样本集(xi, yi), i=1, 2, …, n, xi∈Rd, yi∈{+1, -1}, 是类别标号, d表示空间维度[15]。分类超平面方程表示为:
| $ \mathit{\boldsymbol{w}}{\rm{ }} \times {\rm{ }}\mathit{\boldsymbol{x}}{\rm{ }} + b = 0 $ | (1) |
判别函数的一般形式为:
| $ g\left( x \right) = {\rm{ }}\mathit{\boldsymbol{w}}{\rm{ }} \times \mathit{\boldsymbol{ x}}{\rm{ }} + b $ | (2) |
式中, x是d维特征向量; w称为权向量; b为常数, 称为阈值权。
将判别函数归一化处理使两类所有的样本都满足下式:
| $ {y_i}\left[{\left( {\mathit{\boldsymbol{w}}{\rm{ }} \times {x_i}} \right) + b} \right] -1 \ge 0, i = 1, 2, \ldots, n $ | (3) |
此时的分类间隔为2/‖w‖, 间隔最大等价于‖w‖2最小。函数φ(w)为:
| $ \varphi \left( \mathit{\boldsymbol{w}} \right) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} = \frac{1}{2}\left( {\mathit{\boldsymbol{w}}{\rm{ }} \times {\rm{ }}\mathit{\boldsymbol{w}}{\rm{ }}} \right) $ | (4) |
要找到最优超平面, 即在不等式的约束下, 求函数(4)的最小值。为此, 构造Lagrange函数, 则有:
| $ \begin{array}{l} L\left( {\mathit{\boldsymbol{w}}, b, \alpha } \right) = \\ \frac{1}{2}\left( {\mathit{\boldsymbol{w}} \times \mathit{\boldsymbol{ w}}} \right)- \sum\limits_{i = 1}^n {{\alpha _i}} ({y_i}\left[{\left( {\mathit{\boldsymbol{w}} \times {x_i}} \right) + b} \right] -1) \end{array} $ | (5) |
式中, αi>0为Lagrange系数。对w和b求Lagrange函数的极小值。把式(5)分别对w和b求偏微分并令它们等于0, 就可以把原问题转化为如下的对偶问题:
| $ \left\{ \begin{array}{l} {Q_{{\rm{max}}}}\left( \alpha \right) = \sum\limits_{i = 1}^n {{\alpha _i}}-\sum\limits_{i, j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}({x_i} \times {x_j})} \\ \sum\limits_{i = 1}^n {{y_i}{\alpha _i} = 0, i = 1, 2, \ldots, n} \\ {\alpha _i} \ge 0, i = 1, 2, \ldots, n \end{array} \right. $ | (6) |
若αi*为最优解, 则最优分类函数为:
| $ \begin{array}{l} f\left( x \right) = {\rm{sgn}}\{ ({\mathit{\boldsymbol{w}}^*} \times \mathit{\boldsymbol{x}}) + {b^*}\} = \\ {\rm{sgn}}\left\{ {\sum\limits_{i = 1}^n {{\alpha _i}^*} {y_i}\left( {{x_i} \times \mathit{\boldsymbol{x}}} \right) + {b^*}} \right\} \end{array} $ | (7) |
式中, sgn()为符号函数; 支持向量机对应的αi*均不为0, 非支持向量机对应的αi*均为0;b*是分类的阈值。
在线性不可分的情况下, 某些训练样本不能满足条件式(3), 因此, 在式(3)中增加一个松弛变量εi≥0, 约束条件式成为:
| $ {y_i}\left[{\left( {\mathit{\boldsymbol{w}} \times {x_i}} \right) + b} \right] -1 + {\varepsilon _i} \ge 0, i = 1, 2, \ldots, n $ | (8) |
为了限制样本被错误划分, 对目标函数引入惩罚因子C, 函数式变为:
| $ \varphi \left( {\mathit{\boldsymbol{w}}, \varepsilon } \right) = \frac{1}{2}\left( {\mathit{\boldsymbol{w}} \times \mathit{\boldsymbol{w}}} \right) + C\sum\limits_{i = 1}^n {{\varepsilon _i}} $ | (9) |
式中, C是常数, 可以调节错分样本的惩罚系数, 值越大, 惩罚越大, 其对偶问题可转化为:
| $ \left\{ \begin{array}{l} {Q_{{\rm{max}}}}\left( \alpha \right) = \sum\limits_{i = 1}^n {{\alpha _i}}-\frac{1}{2}\sum\limits_{i, j = 1}^n {{\alpha _i}} {\alpha _j}{y_i}{y_j}({x_i} \times {x_j})\\ \sum\limits_{i = 1}^n {{y_i}{\alpha _i} = 0, i = 1, 2, \ldots, n} \\ 0 \le {\alpha _i} \le C, i = 1, 2, \ldots, n \end{array} \right. $ | (10) |
求解出上述各系数α、w、b对应的最优解α*、w*、b*后, 得到最优分类函数为:
| $ f\left( \mathit{\boldsymbol{x}} \right) = {\rm{sgn}}\left\{ {\sum\limits_{i = 1}^n {} {\alpha _i}^*{y_i}\left( {{x_i}\cdot\mathit{\boldsymbol{x}}} \right) + {b^*}} \right\} $ | (11) |
在求解上述最优化问题时, 常用的核函数主要有线性、多项式、高斯径向基和S形等4种核函数。
2 分类实现与评价 2.1 研究区及数据无人机遥感影像选择四川省绵竹市汉旺镇1 200像素×1 200像素大小的子区域作为试验区, 如图 2所示。Landsat 8 OLI/TIRS遥感影像为杭州地区的B6、B5、B4合成影像, 地物包括房屋、水体、山地和农田等4种类型, 遥感影像如图 3所示。
 |
| 图 2 汉旺地区无人机影像图 Fig.2 UAV Image of Hanwang District |
 |
| 图 3 杭州地区的Landsat 8 OLI/TIRS影像 Fig.3 Landsat 8 OLI/TIRS Image of Hangzhou District |
2.2 数据处理
使用ENVI4.8遥感图像处理软件进行裁剪处理, 得到研究区范围图像。
根据背景资料和预处理结果选择视觉效果最佳的彩色合成图像, 建立各类地物的训练区, 并使训练样本的分布尽量均匀。由于SVM支持小样本分类。因此, 在分类时, 人为干预使相同的地物分类中样本数目相等, 本试验中, 所有地物类别的样本数均通过选点的方式产生且各自对应的样本数均为100。
2.3 结果与评价 2.3.1 无人机影像分类结果与评价为了评价研究方法的分类效果, 分别用最大似然法与SVM法对遥感影像进行分类, 并计算总体精度和Kappa系数进行定量评价。
选取该地区农田、植被、道路、房屋和裸土等5类地物类型, 对应的颜色分别为深绿色、绿色、白色、红色和紫色。最大似然分类与SVM分类结果分别如图 4所示。
 |
| 图 4 无人机影像分类结果 Fig.4 Classification Results of UAV Image |
从无人机影像分类结果可以看出:
1) 最大似然分类对于整块的房屋和道路分类效果较好; 农田分类效果很差, 出现较多的混分区域且分类的碎点很多; 对于植被分类, 右侧道路周围的植被分类较为完好; 对于裸地的分类, 在房屋附近的裸地分类较好。
2) SVM分类结果显示道路、农田、植被和房屋分类效果较好, 能很好地反映边界和轮廓; 对于裸地分类, 房屋周围的裸地提取较好, 但是部分裸地被分为道路, 存在一定的混分现象。
采用混淆矩阵、总体精度和Kappa系数来定量评价最大似然法与SVM的分类效果, 如表 1所示。
| 表 1 汉旺地区最大似然分类精度和SVM分类精度 Tab.1 Classification Accuracy of Maximum Likelihood Method and SVM Method in Hanwang |
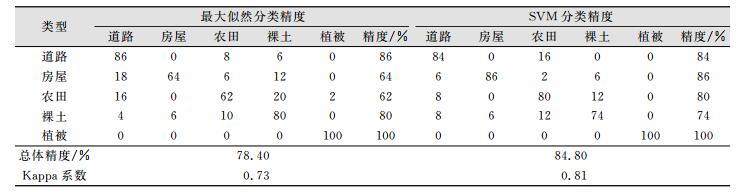 |
从表 1可以看出, 分类的总体精度从78.40%提高到84.80%, 提高了约6%;Kappa系数也相应的从0.73提高到0.81, 提高了约0.08。说明与传统的最大似然分类法相比, 利用SVM分类后, 精度有很大提高。
2.3.2 Landsat 8 OLI/TIRS影像分类结果与评价选取水体、农田、山地和房屋4类地物类型, 分别对应颜色为蓝色、绿色、黄色和红色。最大似然分类法与SVM分类结果如图 5所示。
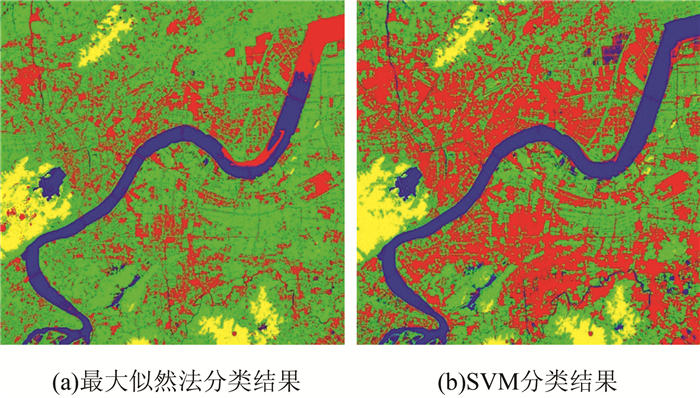 |
| 图 5 Landsat 8 OLI/TIRS影像分类结果 Fig.5 Classification Results of Landsat 8 OLI/TIRS Image |
从Landsat 8 OLI/TIRS影像分类结果可以看出:
1) 最大似然分类结果显示, 山地和水体提取的轮廓相对较好; 对于房屋和农田的分类, 存在相互误分现象。
2) SVM分类结果显示, 山地和水体的提取轮廓相对较好, 水体的分类几乎不存在误分和混分现象; 农田和房屋的分类效果和实际地物匹配程度较高。
最大似然法与SVM的混淆矩阵、总体精度和Kappa系数分别如表 2所示。
| 表 2 杭州地区最大似然分类精度和SVM分类精度 Tab.2 Classification Accuracy of Maximum Likelihood Method and SVM Method in Hangzhou |
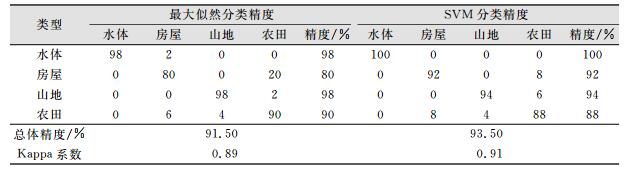 |
从表 2可以看出, 与最大似然法相比, SVM分类的总体精度从91.50%提高到93.50%, 提高了2%;Kappa系数也相应的从0.89提高到0.91, 提高了约0.02。说明与传统的最大似然分类法相比, SVM分类的总体精度有明显提高。
2.4 不同遥感影像分类结果比较1) 从表 1、表 2可以看出, 与传统的最大似然分类方法相比, 利用SVM分类后, 总体精度有很大的提高, 尤其是地物光谱特性差异较大时, 精度的提高明显。
2) 当地物光谱差异达到了一定程度, 不足以影响分类效果时, 最大似然分类方法和SVM分类的效果接近。
3) 最大似然法对光谱特征差异明显的地物分类效果较好, 对光谱特征相近的地物分类效果较差。SVM在给定准确的训练样本的情况下分类效果较好, 相对于最大似然分类法, SVM分类精度有所提高, 但是也受到地物光谱特征的影响。
3 结束语本文从SVM理论出发建立了基于SVM光学遥感影像的分类模型, 利用无人机遥感影像和Landsat 8 OLI/TIRS影像进行分类实验。结果表明, SVM实现了对无人机遥感影像和Landsat 8 OLI/TIRS影像地物的精确提取。这种精度高的方法对光学遥感影像地物精确分类有着广阔的应用前景。
在研究工作中仍然存在两方面问题未能很好解决, 需要进一步的研究和讨论:①增加纹理特征:仅仅依靠光谱信息不能充分地进行分类, 如何更加快速有效提取纹理信息并参与到影像分类, 对提高分类精度起着重要的作用; ②判决函数的改进:如果能研究更有效地判决函数结合改进的训练算法, 将会大大提高分类精度, 对高光谱影像分类用于生产实践意义重大。
| [1] |
李贵东.滩涂资源空间分布信息的遥感提取方法研究与应用—以上海市滩涂资源信息提取为例[D].上海: 华东师范大学, 2007
|
| [2] |
吴今培, 孙德山. 现代数据分析[M]. 北京: 机械工业出版社, 2006.
|
| [3] |
邓乃扬, 田英杰. 数据挖掘中的新方法—支持向量机[M]. 北京: 科学出版社, 2004.
|
| [4] |
张俊, 王宝山, 张志强. 面向对象的高空间分辨率影像分类研究[J]. 测绘信息与工程, 2010, 35(3): 3-5. |
| [5] |
Vapnik V N. Statistical Learning Theory[M]. New York: Wiley, 1998.
|
| [6] |
张勇.基于SVM遥感图像专题信息提取研究[D].长沙: 中南大学, 2005
|
| [7] |
刘江华, 程君实, 陈佳品. 支持向量机训练算法综述[J]. 信息与控制, 2002, 31(1): 45-50. DOI:10.3969/j.issn.1002-0411.2002.01.010 |
| [8] |
刘志刚, 李德仁, 秦前清, 等. 支持向量机在多类分类问题中的推广[J]. 计算机工程与应用, 2004(7): 10-13. DOI:10.3321/j.issn:1002-8331.2004.07.004 |
| [9] |
李毅, 徐守时. 基于支持向量机的遥感图像舰船目标识别方法[J]. 计算机仿真, 2006, 20(6): 180-183. DOI:10.3969/j.issn.1006-9348.2006.06.048 |
| [10] |
杨娜, 秦志远, 张俊. 基于支持向量机无限集成学习方法的遥感图像分类[J]. 测绘科学, 2013, 38(1): 47-50. |
| [11] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.
|
| [12] |
杨长坤, 王崇倡, 张鼎凯, 等. 基于SVM的高分一号卫星影像分类[J]. 测绘与空间地理信息, 2015, 38(9): 142-144. DOI:10.3969/j.issn.1672-5867.2015.09.049 |
| [13] |
严威, 夏晨阳, 吴国宝. 基于核的多尺度纹理特征遥感影像SVM分类[J]. 信息技术, 2015(5): 53-56. |
| [14] |
李萌.基于支持向量机的高分遥感影像分类技术研究与应用[D].北京: 中国地质大学(北京), 2015
|
| [15] |
刘志刚.支撑向量机在光谱遥感影像分类中的若干问题研究[D].武汉: 武汉大学, 2004
|
 2018, Vol. 43
2018, Vol. 43


