| 滑动Neville插值算法在GPS精密星历插值中的应用研究 |
2. 中国地质大学 (武汉) 信息工程学院,湖北 武汉,430074;
3. 内蒙古自治区基础地理信息中心,内蒙古 呼和浩特,010000
2. College of Information Engineering, China University of Geosciences (Wuhan), Wuhan 430074, China;
3. Geomatics Center of Inner Mongolia Autonomous Region, Inner Mongolia 010000, China
国际GNSS服务组织 (International GNSS Service,IGS) 能够提供包括GPS精密星历在内的高质量数据和产品,精密星历共有3种类型,分别是事后精密星历 (IGS)、快速精密星历 (IGR) 及预报精密星历 (IGU),精密星历精度较高,通常情况下可以达到5 cm的精度[1]。每一种精密星历文件都是从整点开始每隔15 min给出一组卫星位置数据,但通常在GPS精密定位中接收机的采样率一般为30 s、15 s,甚至更密[2],因此需要计算采样时刻GPS卫星的精确位置,这是一个至关重要的环节,计算结果的精度将直接影响到定位结果的准确性。
在精密定位中,通过精密星历文件获取卫星的位置一般采用内插法和拟合法,目前常用的内插方法有Lagrange插值和Neville插值[3]。李明峰等[4]指出Lagrange插值和Neville插值实质相同,但当插值阶数增加时,Neville插值的原有计算仍有价值,不需要重新进行计算,而Lagrange插值则需要完全重新计算;雷雨等[5]讨论了利用滑动式Lagrange插值法对GPS精密星历进行插值,这种方法充分考虑了待插值时刻前后的位置信息,插值精度较高;邱蕾等[6]认为Neville算法具有承袭性,算法简单,并推荐在插值精密星历时优先考虑此种方法;宫厚诚和李全海[7]分别使用Lagrange插值、Neville插值、Newton插值3种方法,利用IGS提供的精密星历为基础内插所需时刻的卫星坐标,通过实例分析得出插值点在节点中央时3种方法的插值精度都高;柳迪等[8]介绍了Lagrange和Newton两种插值方法,对IGS精密星历进行了内插,并对插值的结果进行对比分析。通常使用的拟合法有Chebyshev多项式和Legendre多项式拟合[9];赵娟[10]比较了Chebyshev多项式和Legendre多项式插值法;韦建超[11]研究了Chebyshev多项式插值计算精密卫星星历的精度,并将其插值结果与Lagrange插值和Newton插值做了对比分析;卓宁[12]分析比较了Chebyshev多项式插值及Neville算法的数学模型及插值结果,探讨了上述两种插值算法的适用范围。除此之外,也有学者讨论了其他类型的插值方法,蒋瑞波等[13]在2010年计算机应用与系统建模国际会议上阐述了利用傅里叶级数插值计算卫星位置的方法,他们指出这种方法具有很高的插值精度,并可完全取代其他方法;刘伟平等[14]在充分顾及到卫星运动物理特性的基础上,采用三角函数插值法计算卫星位置,实验证明这种方法的内插和外推效果均很好,相比于传统方法而言, 这种方法在外推短时间跨度时具有明显优势。
上述研究都是基于某一种星历文件进行的,尚缺少对于IGS提供的所有3种精密星历插值方面的研究。本文结合滑动式插值的思想及Neville插值增加插值阶次无需重新计算的优势,设计了滑动式Neville插值算法,并利用这种算法分别对IGS提供的3种精密星历数据文件进行了插值研究。
1 插值数学模型 1.1 Neville算法Neville插值是一种线性逐次插值方法,其基本插值思想是通过低一次多项式组合来获得高一次插值多项式。其基本做法是:首先求出若干个一次插值多项式的值,进而利用它们之间的两两组合得到若干个二次插值多项式,随后进一步利用这些二次多项式间的两两组合来得到若干个三次多项式,采用迭代方式进行,这种算法不用算出具体的函数表达式,而直接计算函数在指定点的值,简化了计算过程,如公式 (1)。其基本的插值算法思路为:假设有n+1个节点时刻,分别为t0,t1,…,tn,对应时刻的星历依次为y0,y1,…,yn。令:
| $ {P_{i, j}} = \frac{{(t-{t_j}){P_{i-1, j-1}} - (t - {t_{j - 1}}){P_{i, j - 1}}}}{{{t_{i - j}} - {t_i}}}\;(i, j = 1, 2, \cdots, n) $ | (1) |
计算流程为:
历元时刻第1步第2步第3步…第n步
| $ \begin{array}{*{20}{c}} {{t_0}}&{{P_{0, 0}}}&{}&{}&{}&{}\\ {{t_1}}&{{P_{1, 0}}}&{{P_{1, 1}}}&{}&{}&{}\\ {{t_2}}&{{P_{2, 0}}}&{{P_{2, 1}}}&{{P_{2, 2}}}&{}&{}\\ \vdots & \vdots & \vdots & \vdots &{}&{}\\ {{t_n}}&{{P_{n, 0}}}&{{P_{n, 1}}}&{{P_{n, 2}}}& \cdots &{{P_{n, n}}} \end{array} $ |
当精度不满足要求,而需再增加一个节点时,前面的计算完全有效,并不需要重新计算[15],Neville算法的这种特性也使得计算效率更高。
1.2 滑动插值思想插值算法中插值点位置的选择非常重要,当插值点靠近插值区间的两端时,利用插值函数进行插值则会出现较大的误差,因此应尽可能保证插值节点位于插值区间的中间,以得到较为精确的插值坐标。滑动式插值的基本思想为:利用一个滑动的“窗口”选取插值区间内的数据,确保在每次插值计算时插值节点均位于插值区间的中间。滑动插值示意图如图 1所示,其中箭头所指的是插值时刻,长方形方框内为滑动选择的插值节点。
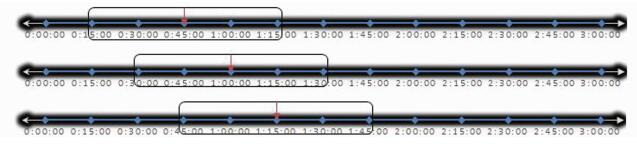 |
| 图 1 3阶滑动插值示意图 Figure 1 Schematic Diagram of 3rd Order Sliding Interpolation |
1.3 滑动Neville插值算法
将滑动插值思想融合到Neville插值算法之中,在计算卫星坐标时,选取待插值时刻左右等量的已知时刻的卫星坐标数据作为插值基点,当插值时刻发生变化时,移动此插值“窗口”,以保证待插值时刻始终在已知卫星点坐标中央。插值阶数增加时,利用前一阶插值运算结果,同时保证插值时刻在“窗口”中央,这样既重复利用了插值计算结果,又保证了插值精度。
2 算例分析本文选择从IGS网站下载的2013年2月13日、14日和15日连续3天的数据进行分析,每天都下载IGR、IGS及IGU 3种精密星历文件,选取14日00:00:00-23:45:00作为插值时段,PRN号为G13的卫星为研究对象,插值的时间跨度为30 min,插值计算每小时内第15 min的星历数据,以每小时内各精密星历文件给出的第15 min坐标数据作为真值,采用完全自主设计的读取数据算法读取文件,利用设计的滑动Neville算法进行插值,并将计算出的数据与真值进行对比分析。图 2是利用滑动Neville算法插值IGR、IGS和IGU精密星历后得到的X坐标残差图,表 1是相应的残差数据表。
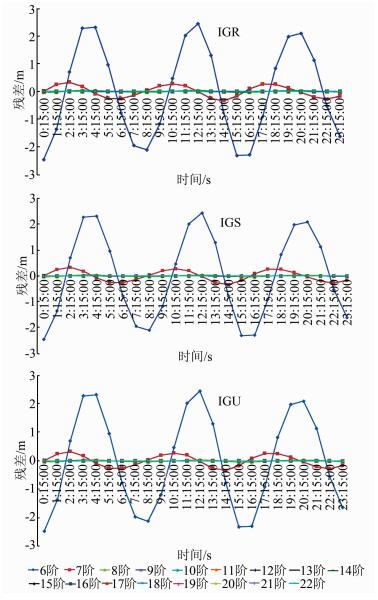 |
| 图 2 IGR、IGS、IGU文件的X坐标残差图 Figure 2 X Coordinate Residual Plots of IGR, IGS, IGU Files |
| 表 1 IGR、IGS、IGU文件X坐标残差表/m Table 1 X Coordinate Residuals Table of IGR, IGS, IGU Files/m |
 |
由图 2可以看出,利用IGR、IGS及IGU精密星历文件,采用滑动Neville算法计算GPS卫星位置时,插值残差的图像走势基本相同。在6阶插值时曲线波动较大,各时段内插值残差抖动较大,坐标残差数量级最大在m级,完全不能满足精密定位的需求。7阶插值时,各时段内插值残差虽有抖动,但能够保持在较小的幅度内,坐标残差的数量级最大在dm级,大于精密星历本身的标称精度,不能够满足精密定位对于插值结果的要求,但相对于6阶插值来说,插值效果已有明显改善。当插值阶次达到8时,由表 1可知,IGR、IGS及IGU星历最大的插值残差分别为4.4 cm、4.3 cm和4.3 cm,均已小于各精密星历文件本身5 cm的标称精度。插值阶次增加到9阶时,由表 1可看出,IGR星历的最大插值误差只有6.3 mm,非常接近真值,IGS和IGU星历最大插值残差分别为6.7 mm和6.3 mm,全都远远小于IGS组织提供的精密星历文件自身的精度误差。而后随着插值阶数的逐步增大,插值效果虽仍有改善,但总体的改善幅度不是很大,插值结果趋于平稳。另外,高阶插值需要选择较多的插值节点,耗费相对较多的内存空间,运算时间也较长,而且随着插值阶数的增加,插值区间中间时间段内虽能够保持精度,但两端时间段内残差逐步增大。
综上所述,对于IGS组织所提供的IGR、IGS及IGU精密星历来讲,一方面从插值精度方面考虑,另一方面顾及插值区间的对称性和计算速度问题,最优的插值阶次均为9阶。
为了能够对比分析各类型精密星历文件在利用滑动Neville算法插值时精度的优劣,选取各类型文件的最优插值阶次,根据计算得出残差最大值及最小值数据结果表如表 2所示,画出各类型文件的残差图如图 3所示。
| 表 2 各类型星历文件X坐标9阶残差数据表/m Table 2 X Coordinate 9-order Residual Data Sheet of Every Ephemeris File/m |
 |
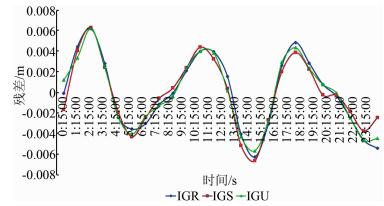 |
| 图 3 各类型文件9阶残差图 Figure 3 9-order Residual Plot of Every Type File |
由图 3及表 2可以得出以下结论,对于各种类型的精密星历文件而言,当取其最优插值阶次时,其插值误差均小于1 cm,每种精密星历文件之间的残差基本相近,说明对于每种精密星历文件来说,当取其最优插值阶次进行插值计算GPS位置时,利用滑动Neville算法插值效果基本相同。
为了研究插值阶次变化时,X、Y和Z坐标插值结果的收敛速度情况,以IGR星历文件为例,利用其插值残差数据,分别绘制了X、Y和Z坐标残差图,如图 4~图 6所示。
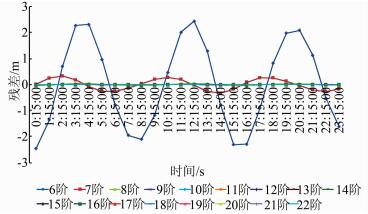 |
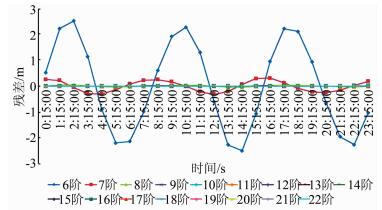
| 图 4 IGR文件X坐标残差图 Figure 4 X Coordinate Residual Plot of IGR File |
 |
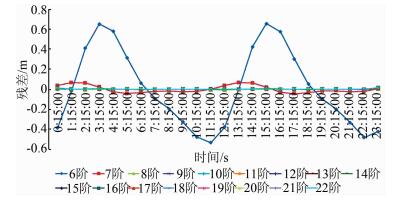
| 图 5 IGR文件Y坐标残差图 Figure 5 Y Coordinate Residual Plot of IGR File |
 |
| 图 6 IGR文件Z坐标残差图 Figure 6 Z Coordinate Residual Plot of IGR File |
由图 4~图 6可以看出,当插值阶次为6时,X及Y坐标方向的插值残差均在m级,而Z坐标方向的残差在dm级,当插值阶次增加到7时,由图 6、表 3及表 1可以看出Z坐标方向最大插值残差已经达到cm级,而X和Y坐标方向的最大插值残差在dm级,当插值阶次增加到8时,X和Y坐标方向最大插值残差均在5 cm以下,能够满足精密定位需求,而Z坐标方向插值残差均在mm级,已经完全能够满足精密定位的需求,而9阶插值时,X和Y坐标方向插值误差才达到mm级。
| 表 3 IGR文件Y及Z坐标残差数据表/m Table 3 Y and Z Coordinates Residual Data Table of the IGR File/m |
 |
以上分析的是IGR精密星历文件插值阶次变化时,X、Y和Z坐标方向不同的插值收敛效果,通过实验发现,当插值阶次如上述情形变化时,IGS及IGU精密星历文件插值收敛效果跟IGR星历文件相同。
3 结束语1) 利用滑动Neville算法低阶次插值IGR、IGS及IGU精密星历文件时,Z坐标方向的插值结果均要优于X及Y坐标方向插值结果。
2) IGR、IGU及IGS精密星历文件的最优插值阶次均为9阶,兼顾了Neville算法的继承性特点,考虑了插值区间的对称性问题。高阶插值虽然能够改善插值结果,但改善幅度并不显著,而且高阶插值需要选择更多的插值节点参与运算,浪费内存空间。
3) 各种精密星历文件在取最优阶次进行插值时,每种星历文件的插值残差基本相同,因此可以说,无论利用哪种精密星历文件,采用滑动Neville算法时,插值效果基本相同。
| [1] | 段兵兵, 兰孝奇. IGS精密卫星轨道精度分析[J]. 工程勘察, 2012, (2): 63–65. |
| [2] | 陈鹏, 陈正阳, 李骁. 一种新的GPS精密星历插值方法[J]. 大地测量与地球动力学, 2009, 29(2): 111–114. |
| [3] | 王晓明, 成英燕, 刘立. 基于阶次组合的GPS精密星历插值研究[J]. 大地测量与地球动力学, 2011, 31(4): 103–106. |
| [4] | 李明峰, 江国焰, 张凯. IGS精密星历内插与拟合法精度的比较[J]. 大地测量与地球动力学, 2008, 28(2): 77–80. |
| [5] | 雷雨, 赵丹宁, 高玉平. 基于滑动式Lagrange插值方法的GPS精密星历内插分析[J]. 测绘工程, 2013, 22(2): 34–36. |
| [6] | 邱蕾, 廖远琴, 花向红. 基于IGS精密星历的卫星坐标插值[J]. 测绘工程, 2008, 17(4): 15–18. |
| [7] | 宫厚诚, 李全海. 基于IGS精密星历的卫星坐标和钟差插值[J]. 全球定位系统, 2009, 34(5): 24–26. |
| [8] | 柳迪, 逄淑涛, 董绪荣. IGS精密星历文件的读取及内插方法研究[J]. 全球定位系统, 2011, 36(5): 46–49. |
| [9] | 冯炜, 薛志宏, 邵佳妮, 等. 两种常用GPS星历拟合方法的精度分析[J]. 大地测量与地球动力学, 2010, 30(1): 145–149. |
| [10] |
赵娟.GPS精密单点定位星历和钟差的研究[D].阜新:辽宁工程技术大学, 2011 |
| [11] |
韦建超. GPS精蜜单点定位的数据处理[D].长沙:中南大学, 2007 |
| [12] | 卓宁. GPS数据处理中卫星精密星历插值方法分析[J]. 战术导弹技术, 2010, (4): 76–79. |
| [13] | Jiang R B, Liu X Q.Using Fourier Series to Fit the GPS Precise Ephemeris[C].ICCASM 2010, Taiyuan, China, 2010 |
| [14] | Liu W, Hao J. A New Interpolation Method Based on Satellite Physical Character in Using IGS Precise Ephemeris[C]. China Satellite Navigation Conference, Guangzhou, China, 2012 |
| [15] | 魏二虎, 柴华. GPS精密星历插值方法的比较研究[J]. 全球定位系统, 2006, 31(5): 13–15. |
 2017, Vol. 42
2017, Vol. 42

