| 重力潮汐数据预处理的自动化程序设计 |
2. 北京四维空间数码有限公司,北京,100039
2. Beijing Siwei Spatial Data Technology Co., Ltd., Beijing100039, China
在日月引力的作用下,地球形体会产生一个像海水起伏一样的周期性变化,这种现象称为固体地球潮汐(简称固体潮)。同样,日月的吸引使得海水发生大面积的平移,再次导致地球内部质量的重新分配而产生海洋潮汐。无论是重力固体潮还是海洋潮汐,均可通过观测得到的重力潮汐数据进行调和分析后求解出潮汐参数(潮汐因子和相位滞后)。精确的固体潮潮汐参数可为地表和空间大地测量提供精确的潮汐改正[1, 2],为反演地球内部结构提供数据[3],也可用于研究地球近周日自由摆动[4]、震源机制[5]等问题,而精确的海潮潮汐参数可计算海潮负荷影响[6],广泛应用于研究沿海地区海潮负荷对地表位移[7]、全球海潮模型的修正[8]、重力合成潮汐参数的精化及地球内部应力应变等研究[9, 10]。对重力数据进行有效的潮汐数据预处理,获得高质量的观测数据,是获得精确潮汐参数的保障。
重力潮汐数据观测过程中受多种因素的影响,如仪器、观测环境、电压等。这些影响导致重力固体潮汐原始记录数据在观测过程中不可避免存在尖峰、间断、阶跃等异常数据,这些异常数据会影响固体潮的数据分析。因此在对固体潮数据进行调和分析之前必须进行有效的预处理,尽可能充分地消除干扰信号,为潮汐数据处理提供高精度的观测资料。实践证明,充分有效的预处理可以大大提高调和分析结果的精度。
近年数据预处理主要使用的预处理方法和软件中,Nakai方法最早用于潮汐数据预处理,Preterna软件包是专用于固体潮汐观测数据预处理的软件包[11]。Tsoft潮汐数据预处理软件是在Preterna软件的基础上研制的,已被国际地潮中心列为GGP项目国际超导重力仪重力潮汐观测资料交换的标准预处理软件[12]。陈晓东等[13]提出一种新的重力潮汐数据预处理和分析方法,Tsoft潮汐数据预处理软件可以有效去除间断、尖峰、突跳等异常数据,预处理可信度较高。熊先保等[14]介绍了固体潮汐观测数据预处理中的常用方法以及利用计算机软件完成了固体潮观测数据的预处理。许闯等[15]研究了重力固体潮汐观测数据的预处理方法,给出了对原始观测数据降采样的平均滤波和小波滤波处理方法以及处理中断数据的线性插值和三次样条插值方法,研制了重力固体潮汐观测数据自动化预处理软件APTsoft,实现了异常数据(包括尖峰、突跳、间断等)的自动标定与改正功能。羊锴等[16]对连续重力观测数据预处理流程进行了介绍,并阐述了连续重力观测数据应用平台中的缺记处理、阶跃处理、突跳处理等方法,初步分离出了五道数据序列,为进一步的潮汐分析、非潮汐变化分析、仪器漂移分析奠定了基础。在以上潮汐数据预处理方法中,以Tsoft潮汐数据预处理软件应用最为广泛,文献[17, 18]先后采用该方法进行潮汐数据的预处理,得到了较好的预处理结果。
目前,现有的固体潮数据预处理软件(除APTsoft外)大多为人工操作,且数据处理人员要有一定的经验性,处理过程较为繁琐,自动化程度不高,耗时耗力。本文以Matlab平台为基础在Tsoft预处理基础上,研制了一套能自动识别数据异常位置,并能一键改正的数据预处理程序——FTsoft,实现了高自动化的数据预处理[19-27]。
1 数据预处理原理由于重力固体潮汐观测数据总是会出现数据异常(主要有尖峰、间断、阶跃等),因此在测定地球潮汐参数之前应对观测记录数据进行预处理,在对观测分析结果精度无影响的前提下,尽可能删除数据中的干扰。重力固体潮汐观测数据数据预处理方法和软件主要有Nakai预处理和分析方法、Preterna预处理软件包、Tsoft预处理软件、数据差分、数据异常处理等。本文主要针对数据异常进行了处理,得到潮汐数据分析所需要的“干净”数据。
1) 观测模拟值的计算。利用Tsoft潮汐数据处理软件,根据该地区已有的潮汐因子和相位滞后经验值计算出潮汐模拟理论值ymod(t),t时刻变化的实际重力潮汐观测值yobs(t)可表示为:
| $ y_{\mathrm{obs}}(t)=y_{\mathrm{mod}}(t)+b P(t)+\varepsilon(t) $ | (1) |
式中,ymod(t)为理论模拟值; bP(t)为大气负荷对重力变化的影响; P(t)为与时间t有关的气压观测值; b为大气重力导纳值; ε(t)为重力残差,重力残差中包含极移对重力的影响、日长对重力的影响、仪器漂移等非潮汐信号。再根据文献[17]分别计算出极移和日长对潮汐的影响,根据式(2)可方便地计算出观测值的模拟值计算值y′obs(t):
| $ y^{\prime}_{\mathrm{obs}}(t)=y_{\mathrm{mod}}(t)+b P(t)+d g_{1}(t)+d g_{2}(t) $ | (2) |
2) 间断处理。对于间断数据的处理,首先对原始数据中的缺省值(数值为99 999.999)进行程序自动识别,找到数据缺省值的位置。程序中已经存储由式(2)计算得到的观测模拟值,识别后程序自动将观测模拟值代替该段数据的缺省值,并将整段数据前后数据连接起来。
3) 阶跃处理。在阶跃处理中,存在两部分阶跃处理:①观测数据自身的阶跃处理; ②整段数据与观测模拟值的阶跃处理。首先将经过间断处理后的数据绘制在程序主界面上,通过眼睛识别判断该段数据存在的阶跃数(从数据的整体来看,整段平均值应固定在某一固定数据,整段数据中,若前后两段数据前后存在明显平均值不一致,则判断为潮汐数据存在阶跃)。根据阶跃点数,将原始观测数据分为若干段,每一段为一个独立数据单元,以第一个数据单元为基准,计算出后续每个数据单元平均值与第一个数据单元平均值的差值,再根据差值将除第一个数据单元外所有数据单元平移到第一个数据单元的平均位置,实现整段数据的平均值基本一致,以完成观测数据自身的阶跃处理。最后以观测数据为基准,将观测模拟值平移至同一基准线上。
4) 尖峰处理。首先将观测模拟值平均值与经过间断、阶跃处理后的观测数据平均值进行比对,以后者为基准,经阶跃处理得到与经过间断、阶跃处理后的观测数据具有相同平均值的新的观测模拟值。再次根据模拟平均值与经过间断、阶跃处理后观测数据的差值标准差设定阈值去粗差,可以设置差值平均值的3倍标准差为阈值,超过阈值平均值用新的观测模拟值来代替,这样根据新的观测模拟值便可求得异常数据处理后的观测值。在尖峰处理过程中,由于大的尖峰数据和间断数据与观测模拟值差值均超过了差值平均值的3倍中误差,所以在尖峰处理过程中,两部分异常数据均得到了很好的修复。
2 数据预处理软件本文采用Matlab语言编写能够实现对重力固体潮观测数据预处理的自动化软件FTsoft。该程序采用面向对象操作界面,界面简洁、处理流程清晰,能够实现对数据间断、阶跃、尖峰等数据异常的自动化处理,简单方便。本文借助Tsoft软件计算出的潮汐模拟理论值和日长、极移对重力潮汐的影响,依次对间断、阶跃和尖峰数据进行处理,最后将处理后的数据保存输出。
3 数据计算与分析本文以武汉九峰台站(大地经度为114.489 8°,大地纬度为30.515 9°)2014年秒采样率的原始观测记录为基础,经过加工后得到实验数据,同时在IERS网站上获得了2014年以日为单位的极坐标(x, y)和TAI、UT1的数值,首先计算出极移、日长对重力观测的影响,并内插为以秒为单位的数据。
图 1中依次给出了原始观测数据和经过Tsoft处理后的结果。从图 1(a)中可以看出,原始观测数据在120 000 s左右(03-27~04-05之间)出现了1次大的间断,在225 000 s左右出现了一次大的尖峰,分别在225 000 s和440 000 s左右出现两次大的阶跃数据,原始观测数据被明显分成3段; 从图 1(b)可以看出,经过间断处理后,间断被此间断前数据的平均值所代替,数据间断得到很好的修复; 经过图 1(c)中的阶跃处理后,第二段和第三段数据被明显拉至第一段数据的水平线上,阶跃得到了很好的修复; 图 1(d)显示了经过间断、阶跃、尖峰处理后的数据,原始观测数据中的间断、阶跃、尖峰等数据均已经得到修复,数据已显得很光滑,特别指出的是,尖峰处理阶段,不但修复了近七段尖峰数据,且在图 1(b)中被平均值连接起来的间断数据也已经被观测值的模拟值所替代,整段数据都得到了较好的预处理; 图 1(e)为图 1(a)经过TSoft预处理后得到的超导重力数据图像,比较图 1(d)和图 1(e)发现,FTsoft软件不但对原始数据中的尖峰、阶跃等数据异常进行了很好的处理,对数据中存在的间断(GAP)等也进行了修复,通过对1(d)和图 1(e)中的数据求差,除了间断数据两者数据相差比较大外,两者处理结果最大的差值为4.5 nm·s-2,这个结果对于潮汐参数的求解等几乎没有影响。
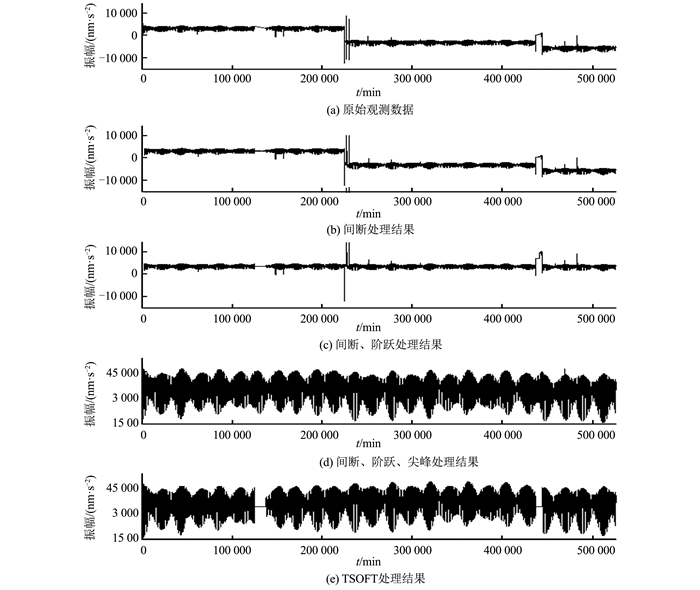 |
| 图 1 FTsoft数据处理结果 Fig.1 FTsoft Processing Results |
为了验证FTsoft预处理效果,以武汉地区2014-01-01~2014-12-31的小时采样数据为例,分别采用FTsoft和Tsoft进行预处理。两者方法均利用Tsoft采用相同的潮汐因子计算理论潮汐,Tsoft采用人机交互方式进行间断、阶跃、尖峰等异常数据的处理,FTsoft采用本研究方法自动实现,最后分别得到原始观测数据的预处理结果。将FTsoft处理结果与Tsoft处理结果分别与观测模拟值求差。Tsoft处理结果与观测模拟值差别在100 nm·s-2左右,FTsoft处理结果与观测模拟值差别在40 nm·s-2左右,相对4 000 nm·s-2的重力固体潮来说,该差别较小; 从相对精度来看Tsoft处理结果与Fsoft处理结果差别在0.6%以下,相对差值较小。进一步对差值求标准差:
| $ s=\sqrt{\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} $ | (3) |
式中, x为Tsoft或FTsoft与观测模拟值的差值;
Tsoft和FTsoft与观测模拟值差值的标准差分别为204.409 0和55.392 9,从数值上来看FTsoft软件比Tsoft软件处理后数据标准差小,在一定程度上FTsoft可代替Tsoft进行潮汐数据预处理。
4 结束语本文从Tsoft数据预处理的流程出发,在Matlab平台研制了一套固体潮潮汐数据预处理的自动化软件FTsoft软件。该软件可以自动识别数据阶跃点数、自动修正间断和尖峰数据。FTsoft软件具备潮汐原始观测异常数据一键化处理的功能,省时省力,提高了工作效率。实践证明,FTsoft处理结果与原始观测值差值标准差比Tsoft处理结果与原始观测值差值标准差小,进一步证明了FTsoft软件的有效性。
| [1] |
张宏伟.海岛重力测量数据的预处理与分析[D].郑州: 信息工程大学, 2012
|
| [2] |
邓洪涛, 赵珞成, 罗志才. 中国海域岛礁重力测量及潮汐改正[J]. 测绘地理信息, 2018, 43(1): 15-19. |
| [3] |
孙和平, 徐建桥, 崔小明. 重力场的地球动力学与内部结构应用研究进展[J]. 测绘学报, 2017, 46(10): 1 290-1 299. |
| [4] |
徐建桥, 孙和平, 罗少聪. 海潮负荷对自由核章动参数拟合的影响[J]. 测绘学报, 2001, 30(3): 214-219. DOI:10.3321/j.issn:1001-1595.2001.03.006 |
| [5] |
张贝, 张怀, 石耀霖. 基于数值模拟的潮汐应力触发月球深震机制的探讨[J]. 中国科学院大学学报, 2016, 33(1): 82-88. |
| [6] |
杨锦玲, 关玉梅, 钟继茂, 等. 厦门重力固体潮海潮负荷改正研究[J]. 地球物理学进展, 2016, 31(3): 992-998. |
| [7] |
周江存, 孙和平. 近海潮汐效应对测站位移的负荷影响[J]. 地球物理学进展, 2007, 22(5): 1 340-1 344. |
| [8] |
周江存, 孙和平. 用东海和南海潮汐资料修正全球海潮模型对中国及邻区重力场负荷计算的影响[J]. 地震学报, 2005, 27(3): 332-338. DOI:10.3321/j.issn:0253-3782.2005.03.012 |
| [9] |
周江存, 孙和平. 武汉台长周期重力固体潮观测的海潮负荷改正[J]. 大地测量与地球动力学, 2007, 27(6): 28-32. |
| [10] |
周江存, 孙和平, 徐建桥, 等. 海潮负荷对地球内部潮汐应力和应变的影响[J]. 地震学报, 2014, 36(3): 433-442. DOI:10.3969/j.issn.0253-3782.2014.03.009 |
| [11] |
Wenzel H G. The Nanogal Software: Earth Tide Data Processing Package Eterna3.30[J]. Bulletin d'Information de Marees Terrestres, 1996, 124: 9 425-9 439. |
| [12] |
Venedikov A P, Vieira R, Toro C L, et al. A New Program Developed in Madrid for Tidal Data Processing[J]. Bulletin d'Informations des Marées Terrestres, 1995, 189: 9 669-9 704. |
| [13] |
陈晓东, 孙和平. 一种新的重力潮汐数据预处理和分析方法[J]. 大地测量与地球动力学, 2002, 22(3): 83-87. |
| [14] |
熊先保, 黄晓华, 牛其寿, 等. 固体潮观测数据预处理中的常用方法及计算机实现[J]. 地震地磁观测与研究, 2006, 27(4): 98-101. DOI:10.3969/j.issn.1003-3246.2006.04.018 |
| [15] |
许闯, 罗志才, 林旭, 等. 重力固体潮观测数据的自动化预处理[J]. 武汉大学学报·信息科学版, 2013, 38(2): 157-161. |
| [16] |
羊锴, 韦进. 基于连续重力观测数据应用平台的数据预处理[J]. 中国科技信息, 2015(Z2): 72-73. |
| [17] |
田桂娥, 孙和平, 陈晓东. 武汉重力固体潮长周期潮汐参数的确定法[J]. 大地测量与地球动力学, 2005, 25(4): 99-104. |
| [18] |
高熹微.重力非潮汐连续信号的提取与分析[D].北京: 防灾科技学院, 2017
|
| [19] |
王鹏磊.基于Matlab的改进导线网平差程序设计[C]. 2013中国地理信息产业大会, 潍坊, 山东, 2013
|
| [20] |
李建章. 基于Matlab的导线网平差程序设计[J]. 兰州交通大学学报, 2010, 29(4): 88-90. DOI:10.3969/j.issn.1001-4373.2010.04.021 |
| [21] |
艾松涛, 黎展荣, 张沛. 加密导线网平差程序的设计与实现[J]. 测绘信息与工程, 2002, 27(6): 8-10. DOI:10.3969/j.issn.1007-3817.2002.06.004 |
| [22] |
史建青, 董春来. 基于Matlab的导线网平差设计与试验研究[J]. 测绘通报, 2012(S1): 142-144. |
| [23] |
杨光亮, 周莉娟, 申重阳, 等. 连续重力信号的非潮汐信息自动提取[J]. 大地测量与地球动力学, 2011, 31(3): 75-78. |
| [24] |
刘少明, 申重阳, 喻节林. VAV03和TSoft软件在重力和形变资料潮汐分析中的应用[J]. 大地测量与地球动力学, 2012, 32(S1): 103-108. |
| [25] |
许闯, 罗志才, 周浩, 等. 重力固体潮观测数据预处理的滤波方法比较[J]. 测绘科学, 2014, 39(6): 12-17. |
| [26] |
常金龙, 姜博, 胡宝慧. 基于NAKAI拟合模型的固体潮汐观测数据补值与延拓的应用研究[J]. 大地测量与地球动力学, 2016, 36(4): 346-349. |
| [27] |
张保军, 王泽民, 安家春, 等. 南极长城站验潮站数据处理和潮汐特点初步分析[J]. 极地研究, 2016, 28(4): 498-504. |
 2020, Vol. 45
2020, Vol. 45

