| 激光点云和图像处理技术在隧道超欠挖检测中的应用研究 |
2. 武汉大学地球空间信息技术协同创新中心, 湖北 武汉, 430079;
3. 武汉大学电子信息学院, 湖北 武汉, 430079;
4. 武汉中观自动化科技有限公司, 湖北 武汉, 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan University, Wuhan 430079, China;
3. School of Electronic Information, Wuhan University, Wuhan 430079, China;
4. Wuhan Zhongguan Automation Technology Co., Ltd., Wuhan 430079, China
隧道超欠挖直接影响隧道的围岩稳定性和施工成本[1], 严格控制超欠挖量对顺利施工、节约资源以及安全生产具有重要意义。传统的隧道超欠挖检测主要以人工测量的方式为主, 采用全站仪、断面仪和测量机器人等设备, 以逐点、逐断面的方式对隧道进行全断面测量, 该类方法检测效率低、耗时长, 需要耗费大量人力、物力[2-4]。此外, 传统检测方法的测量精度易受到隧道环境因素的影响, 不能反映隧道的整体形态变化等情况, 无法满足在隧道开挖过程中大量超欠挖检测的实际需求。相较于传统检测方法, 三维激光扫描技术具有非接触量测、数据精度高、数据获取速度快、数据量大等特点[5-7]。因此在隧道的超欠挖检测以及变形监测等方面得到了广泛应用。
目前, 大多数基于激光点云数据进行隧道超欠挖检测的方法, 都是通过一定方法提取隧道实测点云数据的连续断面, 并与设计断面数据进行比较, 计算隧道的超欠挖量。文献[8]提出一种基于CAD平台进行二次开发来计算隧道超欠挖的方法, 首先将断面实测点连接成线, 然后将所围成的图形与设计图形比较, 求取相应部分超欠挖面积, 再将算法与CAD相结合, 实现计算过程的自动化和可视化。文献[9]提出一种高速公路隧道的超欠挖检测方法, 首先将隧道点云投影到XOY和YOZ平面上, 然后采用Canny边缘检测算法提取投影点云边缘轮廓线, 再将提取的轮廓线导入AutoCAD中, 采用射线相交的方法来计算隧道超欠挖量。文献[10]利用隧道设计中线与隧道实测中线之间相对稳定的位置关系, 提取断面结构线并与设计断面对比, 然后采用Vatti clipping algorithm算法自动进行隧道的超欠挖面积统计。通过将上述方法提取隧道断面并与设计断面进行比较, 过程较为繁琐且耗时久, 虽然在一定程度上实现了隧道超欠挖的自动检测和计算, 但仍然无法从整体上反映隧道的超欠挖情况。
本文提出一种基于激光点云和图像处理技术的隧道超欠挖检测方法, 首先采用三维激光扫描仪对施工中的隧道进行整体扫描, 获取隧道点云数据; 然后将实测点云数据与隧道三维设计模型数据配准后沿坐标轴展平, 通过规则格网内插的方法将展平后的隧道点云数据生成隧道超欠挖灰度图像, 再根据连通域标记等图像处理技术进行隧道的超欠挖量检测并统计超欠挖面积和体积, 根据阈值用不同颜色对超欠挖区域进行渲染显示。相较于传统的检测方法, 检测效率得到较大提升, 并可直观反映隧道整体的超欠挖情况和自动计算隧道的超欠挖量, 测量精度满足隧道超欠挖检测的要求。
1 点云数据的预处理通常情况下, 在隧道实际的施工过程中, 隧道开挖断面无法与设计断面保持完全一致, 形状及位置上都会产生一定的误差。因此在隧道开挖过程中需要对隧道进行超欠挖检测, 进而判断隧道实际施工是否满足隧道设计标准的要求。隧道超欠挖分为超挖和欠挖两种情况, 超挖是指实测隧道断面大于设计断面; 欠挖是指实测隧道断面小于设计断面[11], 以圆形隧道为例如图 1所示。
 |
| 图 1 隧道超欠挖示意图 Fig.1 Diagram of Overbreak and Underbreak Detection |
1.1 坐标系的定义
激光点云数据采用三维激光扫描系统的仪器坐标系来作为坐标基准, 但不同仪器采用的坐标基准也存在较大差异。为便于计算, 本文将直角坐标系定义如下:坐标系的原点位于激光束发射处, Z轴位于仪器横向扫描面内, 其正方向代表隧道的开挖行进方向; X、Y轴均位于仪器的纵向扫描面内, 如图 2所示。
 |
| 图 2 隧道直角坐标系 Fig.2 Rectangular Coordinate System of Tunnel |
为了便于后期的超欠挖检测, 需要将实测的隧道点云数据转换为隧道超欠挖平面点云数据, 其坐标系定义如图 3所示, 其中Z轴代表每个点的超欠挖值, 向上为正, 代表超挖; 向下为负, 代表欠挖。
 |
| 图 3 展平后的点云坐标系 Fig.3 Point Cloud Coordinate System After Flattening |
1.2 点云数据的展平
根据隧道设计断面文件, 通过三维绘图软件将其沿隧道开挖行进方向进行拉伸, 绘制隧道的三维设计模型, 如图 4所示。然后通过三维数据处理软件将实测隧道点云数据和三维设计模型进行配准, 配准结果如图 5所示。
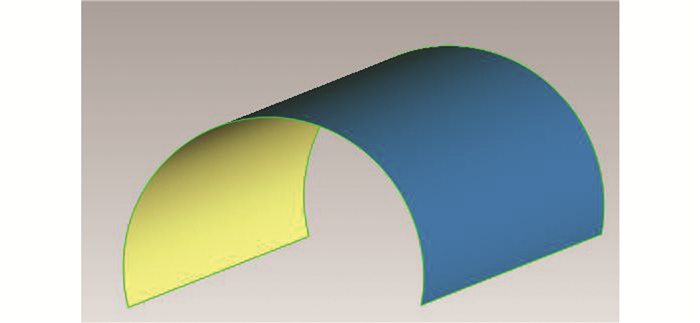 |
| 图 4 隧道三维设计模型 Fig.4 Three-Dimensional Design Mock-up of Tunnel |
 |
| 图 5 配准后的点云数据 Fig.5 Point Cloud Data After Registration |
根据隧道的几何特性, 将配准后的隧道实测点云沿X轴方向展平, 假设原始点云数据中任意一点P的坐标为(x, y, z), 转换后的点云数据中对应点P′的坐标为(X, Y, Z), 则转换后的点云数据可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {\theta = \arctan \frac{y}{x}}\\ {\rho = \sqrt {{x^2} + {y^2}} }\\ {X = \rho \times \theta }\\ {Y = z}\\ {Z = \rho - {R_d}} \end{array}} \right. $ | (1) |
式中, ρ和θ分别表示P点处的距离和角度(弧度); Rd为隧道的理论开挖半径; Z表示超欠挖量的大小。展平后的点云数据如图 6所示, 颜色深浅表示超欠挖量的大小。
 |
| 图 6 展平后的点云数据 Fig.6 Point Cloud Data After Flattening |
2 隧道超欠挖灰度图像的生成
通过规则矩形格网内插[12]的方法将展平后的隧道点云数据生成超欠挖影像, 展平后的点云数据中Z值表示隧道的超欠挖量大小, 如图 7和图 8所示。任意一个点Pij的平面坐标(Xi, Yi)可根据该点在规则格网中的行号j和列号i推算求得:
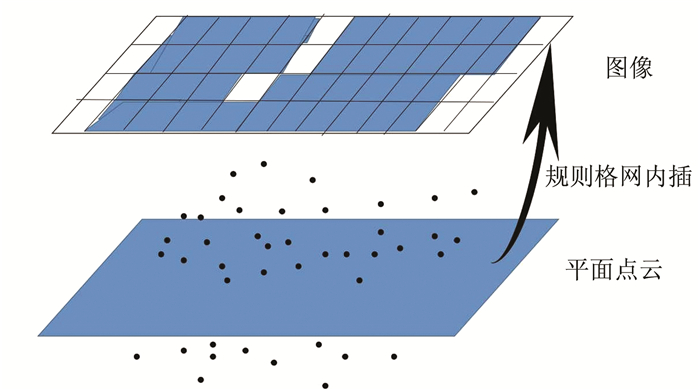 |
| 图 7 超欠挖图像的生成 Fig.7 Image Production of Overbreak and Underbreak |
 |
| 图 8 规则矩形格网 Fig.8 Regular Rectangular Grid |
| $ \left\{ {\begin{array}{*{20}{l}} {{X_i} = {X_0} + i \times {D_X}, i = 0, 1, \cdots {N_X} - 1}\\ {{Y_i} = {Y_0} + j \times {D_Y}, j = 0, 1, \cdots {N_Y} - 1} \end{array}} \right. $ | (2) |
式中, X0和Y0分别为格网起始点的坐标; NY和NX分别为矩形格网的行数和列数; DX和DY分别是指格网在X方向和Y方向的间距, 本文中规则格网的采样间距相等, 所以DX=DY=20 mm。
规则矩形格网内插在数学上属于插值问题, 目的是通过参考点上的超欠挖量求出其他待定点上的超欠挖量。由于采集的隧道原始点云通常是无序的, 为了获取规则的矩形格网, 数据的内插是非常关键的步骤。本文采用反距离加权平均的方法[13]进行插值:
| $ {Z_p} = \frac{{\sum\limits_{i = 1}^n {{p_i}} {Z_i}}}{{\sum\limits_{i = 1}^n {{p_i}} }} $ | (3) |
式中, n为邻近数据点个数; pi为第i个数据点的权值; Zi为第i个数据点的超欠挖值大小。
对应的权值函数为:
| $ {P_i} = {\left( {\frac{{R - {d_i}}}{{{d_i}}}} \right)^2} $ | (4) |
式中, R是选点半径, 本文中所采用的选点半径为40 mm; d为待定点到数据点的距离。
对规则矩形格网中每一个格网点, 从离散的数据点中选取与该规则格网点所对应的几个分块格网中的点, 并将坐标原点移至该格网点P(Xp, Yp), 则有:
| $ \left\{ {\begin{array}{*{20}{l}} {\overline {{X_i}} = {X_i} - {X_p}}\\ {\overline {{Y_i}} = {Y_i} - {Y_p}} \end{array}} \right. $ | (5) |
为了选取邻近的数据点, 以待定点P为圆心, 以R为半径画一个圆形区域(图 9), 所有落在圆内的数据点即被选用。当数据点P(X, Y)到待定点P(Xp, Yp)的距离
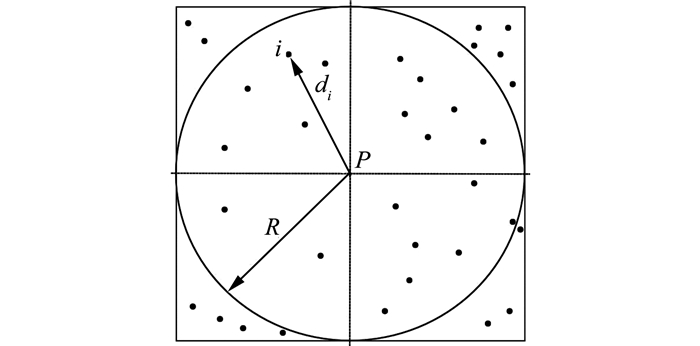 |
| 图 9 数据点的选取 Fig.9 Selection of Data Points |
| $ {d_i} = \sqrt {\bar X_i^2 + \bar Y_i^2} < R $ | (6) |
时, 该点即被选用。若选择的点数不够, 则应增大R的数值, 直至数据点的个数n满足要求。
为了生成隧道超欠挖灰度图像, 需要将内插后的Z值归一化至0~255内, 公式如下:
| $ {\bar Z_i} = \left( {\frac{{{Z_i} - {Z_{{\rm{min }}}}}}{{{Z_{{\rm{max }}}} - {Z_{{\rm{min }}}}}}} \right) \times 255, i = 0, 1, \cdots , n $ | (7) |
然后将归一化后的灰度值赋给相应平面坐标为(Xi, Yi)处的像素, 则生成了隧道超欠挖灰度图像, 如图 10所示, 其中黑色部分代表欠挖, 相对明亮部分代表超挖。
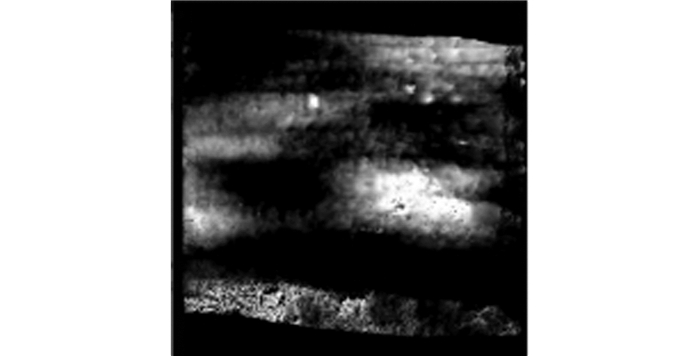 |
| 图 10 超欠挖灰度图像 Fig.10 Gray Image of Overbreak and Underbreak |
3 隧道超欠挖区域的检测与统计
二值图像是灰度图像经过阈值分割后得到的一类只有黑白两种像素值的特殊灰度图像, 具有数据结构简单、数据量小和易于存储等特点, 因此在图像分析与模式识别等领域中有着重要的应用[14]。
按照京张隧道施工过程中对隧道超欠挖区域范围的要求, 对在某区间范围内满足条件的超欠挖区域视为符合安全标准且不作处理, 即将超欠挖灰度图划分为超挖、欠挖和正常三部分。首先对生成的隧道超欠挖灰度图进行两次阈值分割, 分别生成超挖和欠挖部分的二值图像, 结果如图 11所示。然后对二值图像进行形态学闭运算来消除物体内细小空洞并连接邻接物体, 再通过连通域分析方法[15-18]来标记不同的隧道超欠挖区域, 进而统计相应区域的面积和体积。经过闭运算处理后的二值图像结果如图 12所示。
 |
| 图 11 二值图像 Fig.11 Binary Image |
 |
| 图 12 闭运算处理后的二值图像 Fig.12 Binary Image After Close Operation |
结合隧道超欠挖图像的特点, 采用四邻域连通标记的方法对处理后的隧道超欠挖二值图像分别统计隧道超挖和欠挖区域中每个连通部分所包含的像素个数, 则隧道超欠挖的面积为每个像素面积的大小与该部分所包含像素个数乘积; 隧道超欠挖的体积为每个像素面积与所对应位置的Z值和的乘积。
| $ \left\{ {\begin{array}{*{20}{l}} {s = {s_{{\rm{pixel }}}} \times n}\\ {v = {s_{{\rm{pixel }}}} \times \sum\limits_{i = 1}^n {{Z_i}} } \end{array}} \right. $ | (8) |
式中, s和v分别表示连通区域的面积和体积; spixel为每个像素块的面积大小; n为该连通区域中所包含的连通像素个数; Zi为该连通区域中所包含的每个连通像素所对应的超欠挖值的大小。
超欠挖总面积为每个连通区域的面积和, 同理, 隧道超欠挖总体体积为每个连通区域所对应的体积和, 公式如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_{总}} = \sum\limits_{i = 1}^n {{s_i}} }\\ {{V_{总}} = \sum\limits_{i = 1}^n {{v_i}} } \end{array}} \right. $ | (9) |
式中, S总和V总分别表示隧道的超欠挖总面积和总体积; si和vi分别为每个超挖或欠挖区域所对应的面积和体积。
4 实验结果与分析 4.1 实验概况隧道在施工过程中由于人工测量及环境等因素会造成一定的误差, 影响隧道施工质量, 因此需要对施工中的隧道进行超欠挖实时监测, 以确保隧道的施工符合规范要求, 对不满足要求的区域及时进行处理。本文采用地面激光扫描仪对正在施工中的京张铁路某段隧道进行现场扫描, 隧道现场扫描情况如图 13所示。每测站扫描时间约为3 min, 扫描的隧道长度约为30 m, 相对测量精度约为3~5 mm, 满足超欠挖检测的精度要求。地面三维激光扫面仪实测的隧道点云数据约500万个点, 滤波后约为100万个点。
 |
| 图 13 数据采集图 Fig.13 Image of Data Acquisition |
4.2 隧道超欠挖区域的检测
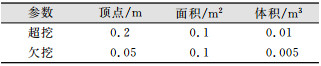
根据京张隧道相关施工标准, 将隧道的超挖与欠挖重新按照表 1中的参数定义, 即当满足表 1中所列的参数时, 则认为相应部分为超挖或欠挖区域。当对应区域的最大Z值大于0.2 m, 面积大于0.1 m2, 体积大于0.01 m3时, 则认为该区域为超挖; 当对应区域的最大Z值小于-0.05 m, 面积的大于0.1 m2, 体积大于0.005 m3时, 则认为该区域为欠挖。对预处理后二值图像按照上述参数要求进行连通域标记后, 对图像和点云数据进行渲染。渲染后的超欠挖结果如图 14所示, 其中红色区域代表超挖, 黄色区域代表欠挖, 绿色区域表示符合隧道施工要求。
| 表 1 超欠挖阈值参数 Tab.1 Threshold Parameters of Overbreak and Underbreak |
 |
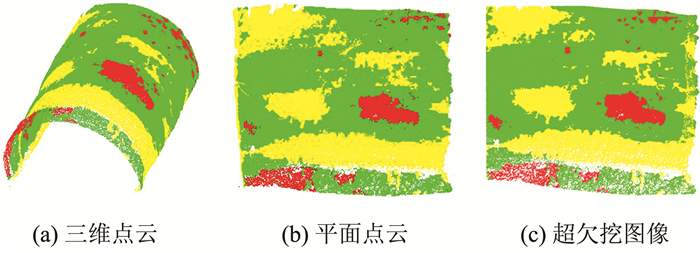 |
| 图 14 渲染结果 Fig.14 Rendering Results |
根据图 14, 可以很容易地从整体判断隧道的超挖和欠挖区域, 进而有效地指导隧道施工, 并对超欠挖区域进行及时处理, 保障工作安全有效地进行。
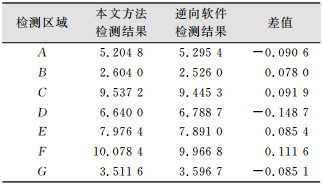
为了验证算法的有效性及实时性, 以面积统计结果为例, 选取如图 15所示的4块超欠挖区域进行面积检测, 并将实验结果与Geomagic Studio软件计算的面积进行比较, 对比结果如表 2所示。Geomagic Studio软件通过计算多边形对象的表面积或投影至指定平面的表面积, 先将选择区域的点云数据进行封装(即将点云转为网格以将点对象转成多边形对象), 然后求取相应部分的面积。其中最大面积偏差为-0.148 7 m2, 最小面积偏差为0.078 m 2, 因此本文方法的检测精度能够满足隧道超欠挖检测的应用需要。为了验证算法的实时性, 本文选用京张隧道某区间段的隧道点云数据进行测试, 滤波后的数据约100多万个点, 本文算法共耗时47.253 7 s, 其中生成规则格网内插及点云渲染耗时46.546 2 s, 超欠挖区域的面积及体积计算耗时0.707 5 s。因此本文方法满足施工过程中隧道大量超欠挖检测工作的要求。
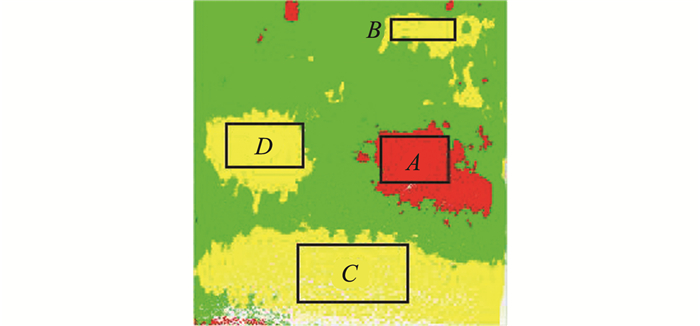 |
| 图 15 部分区域选择 Fig.15 Partial Area Selection |
| 表 2 实验结果对比/m2 Tab.2 Results of Comparison Experiment/m2 |
 |
5 结束语
传统的隧道超欠挖检测方法, 无法满足正在施工中的隧道大量的实时性超欠挖检测, 而且不能从整体上反映隧道的超欠挖情况。本文提出了一种基于三维激光扫描和图像处理技术的隧道超欠挖自动实时检测方法, 选取了京张铁路某区间隧道作为研究区, 并对该方法的有效性和可靠性加以验证, 结果表明, 相较于传统人工和基于隧道断面的检测方法, 该方法通过对点云数据进行渲染以区分超欠挖区域, 整体上更加直观地反映了隧道的超欠挖情况, 检测效率高, 检测结果符合施工隧道的超欠挖检测要求, 并且极大地降低了工作量以及对检测人员的操作要求。
| [1] |
孙少锐, 吴继敏, 魏继红. 隧洞围岩分类与洞径和超欠挖之间的关系研究[J]. 岩土力学, 2005, 26(8): 1 278-1 282. |
| [2] |
许磊, 王长进. 隧道断面自动提取方法研究[J]. 铁道工程学报, 2016, 33(8): 94-99. DOI:10.3969/j.issn.1006-2106.2016.08.019 |
| [3] |
胡琦佳.三维激光扫描技术在隧道工程监测中的应用研究[D].成都: 西南交通大学, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10613-1013252179.htm
|
| [4] |
夏国芳, 王晏民. 三维激光扫描技术在隧道横纵断面测量中的应用研究[J]. 北京建筑工程学院学报, 2010, 26(3): 21-24. DOI:10.3969/j.issn.1004-6011.2010.03.005 |
| [5] |
刘欢, 王立娟, 裴尼松, 等. 三维激光扫描技术在米仓山特长隧道施工中的可行性应用研究[J]. 测绘通报, 2017(9): 83-87. |
| [6] |
Kang Z, Zhang L, Lei T, et al. Continuous Extraction of Subway Tunnel Cross Sections Based on Terrestrial Point Clouds[J]. Remote Sensing, 2014, 6(1): 857-879. |
| [7] |
姜波. 三维激光扫描技术在沈阳地铁测量中的应用[J]. 测绘地理信息, 2017, 42(6): 114-116. |
| [8] |
方成龙. 利用CAD二次开发程序计算超欠挖的研究[J]. 测绘地理信息, 2014, 39(1): 67-68. |
| [9] |
Wang W, Wang Z, Han Y, et al. Continuous Section Extraction and Over-Underbreak Detection of Tunnel Based on 3D Laser Technology and Image Analysis[C].SPIE/IS&T Electronic Imaging, International Society for Optics and Photonics, New York, 2015
|
| [10] |
许磊, 王长进. 基于激光点云的隧道超欠挖检测方法研究[J]. 铁道工程学报, 2016, 33(12): 77-81. DOI:10.3969/j.issn.1006-2106.2016.12.017 |
| [11] |
Maerz N H, Ibarra J A, Franklin J A. Overbreak andUnderbreak in Underground Openings Part 1: Measurement Using the Light Sectioning Method and Digital Image Processing[J]. Geotechnical & Geological Engineering, 1996, 14(4): 307-323. |
| [12] |
张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉: 武汉大学出版社, 2009: 186-189.
|
| [13] |
王琦. LiDAR点云生成格网DEM模型的内插算法研究[D].武汉: 中国地质大学, 2010 http://cdmd.cnki.com.cn/Article/CDMD-10491-2010250634.htm
|
| [14] |
刘奇琦, 龚晓峰. 一种二值图像连通区域标记的新方法[J]. 计算机工程与应用, 2012, 48(11): 178-180. DOI:10.3778/j.issn.1002-8331.2012.11.038 |
| [15] |
牛连强, 彭敏, 孙忠礼, 等. 利用游程集合的标号传播实现快速连通域标记[J]. 计算机辅助设计与图形学学报, 2015, 27(1): 128-135. |
| [16] |
何立风, 高启航, 赵晓, 等. 一种二值图像物体形状特征计算方法[J]. 陕西科技大学学报, 2018, 36(1): 143-147. DOI:10.3969/j.issn.1000-5811.2018.01.027 |
| [17] |
吕常魁, 徐岩, 罗冰心. 基于游程的连通区域标记两次扫描快速算法[J]. 华南理工大学学报:自然科学版, 2017, 45(7): 84-89. |
| [18] |
张奎, 陈兆学. 一种基于游程码的二值图像孔洞标记和表达方法[J]. 光学技术, 2017, 43(4): 364-368. |
 2020, Vol. 45
2020, Vol. 45


