| 基于小波去噪的改进的双曲线沉降预测模型 |
2. 南京宁图信息技术有限责任公司, 江苏 南京, 211100;
3. 中国石油大学地球科学与技术学院, 山东 青岛, 266580
2. Nanjing Ningtu Information Technology Co., Ltd., Nanjing 211100, China;
3. School of Geosciences, China University of Petroleum, Qingdao 266580, China
回归分析法预测模型作为最基本的预测模型,其算法简单,实现起来较为方便,且有较好的预测效果,被广泛应用于各项工程的沉降预测[1]。但其方法较多,各种预测模型适应范围也不一样,带来的预测精度也不同,预测精度高的预测模型需要进行验证,并需要通过公式改进来增加模型的适应范围和预测精度。函数模型主要有多项式趋势模型、对数趋势模型、幂函数趋势模型、指数函数趋势模型、双曲线趋势模型、修正指数模型以及Logistic模型等,本文在这些模型的基础上进行了思考和改进,由于观测数据带有粗差,而这些点代入预测模型极大地影响了预测曲线的走势,所以必须将其剔除,采用小波去噪的方法进行消噪,然后对消噪后的数据进行重采样,获得新的时间序列数据,根据这些新的数据列选用不同预测模型进行沉降预测。通过比较分析发现,常用的几种回归分析预测模型预测效果都不理想,对数函数趋势模型和多项式趋势模型前期预测精度高,后期效果不佳,幂函数和指数函数预测模型预测前后期精度都不佳,双曲线预测模型虽然后期达到预期效果,但前期预测结果与实际观测偏差较大。针对这些不足,本文提出了一种基于小波去噪的改进的双曲线沉降预测模型,为双曲线模型引入一个系数,该系数由荷载决定,通过调整系数的大小来改变预测模型的参数,从而达到最佳的预测效果,实验结果表明,利用改进的方法,预测精度有所提高。
1 小波去噪小波分析因有良好的时频效应,在形变分析中的应用取得了很好的效果。通过对原始数据进行小波分解,得到各尺度系数,然后进行阈值处理,小波重构后得到去噪后的时间序列数据,有效过滤掉观测过程中的信号噪声,提高变形预测的精度[2]。小波变换的含义是把某一称为基本小波的函数作位移τ后,再在不同尺度α下,与待分析信号X(t)作内积,即
| $ W{T_x}(a, \tau ) = \frac{1}{{\sqrt a }}\int_{ - \infty }^{ + \infty } x (t) \times \varphi \left( {\frac{{t - \tau }}{a}} \right){\rm{d}}t $ | (1) |
式中,a>0,称为尺度因子,其作用是对基本小波φ(t)函数作伸缩;τ反应位移,其值可正可负。a、τ都是连续的变量,故又称为连续小波变换。在不同尺度下小波的持续时间随值的加大而增宽,幅度则与
常用的阈值去噪函数有软阈值和硬阈值法。硬阈值去噪法是当小波系数的绝对值小于给定阈值时,令其为零;大于阈值时,则令其保持不变,即:
| $ {w_\lambda } = \left\{ {\begin{array}{*{20}{l}} {w, |w| \ge \lambda }\\ {0, |w| < \lambda } \end{array}} \right. $ | (2) |
软阈值去噪法是当小波系数的绝对值小于给定阈值时,令其为零;当其大于阈值时,则令其都减去阈值,即:
| $ {w_\lambda } = \left\{ {\begin{array}{*{20}{l}} {[{\mathop{\rm sgn}} (w)](|w| - \lambda ), |w| \ge \lambda }\\ {0, |w| < \lambda } \end{array}} \right. $ | (3) |
双曲线法是变形预测中最常用的一种预测模型,是一种纯经验的曲线拟合方法,曲线形态近似一条双曲线,该模型的优点在于它是一个收敛函数,预测效果符合实际,并且后期预测精度很高,但同时也存在一些缺点,由于模型曲线特征明显,会导致前期预测误差很大[4],其数学公式如下:
| $ {Y_t} = a + b/t $ | (4) |
将式中1/t看成一个整体, 通上述方法可求得系数a和b,将系数代入公式即可对后期测量值进行预测[5]。
针对双曲线预测模型前期预测精度不高的问题,本文对该模型进行了改进,对因变量累计沉降量Yt取倒数作为新的因变量,将初始观测值考虑在内,同时引入一个系数ξ,该系数由荷载结合实际情况而定,通过改变该ξ值的大小,来调整双曲线预测公式的系数a和b,使得预测曲线更符合实际,提高预测精度,然后将系数代入公式,对后期沉降值进行预测[6],其公式如下:
| $ {Y_t} = {Y_0} + \xi \frac{{t - {t_0}}}{{a + b\left( {t - {t_o}} \right)}} $ | (5) |
式中,Yt表示累计沉降量;Y0表示初始观测的沉降量;t0表示初始观测的时间;ξ表示荷载系数,该值由实际情况的荷载决定大小,例如水闸的蓄水力;a、b表示预测公式中的参数,通过线性回归计算求得[7]。
将式(5)进行变换,得:
| $ \frac{\xi }{{{Y_t} - {Y_0}}} = \frac{a}{{t - {t_0}}} + b $ | (6) |
式中,
| $ {Y_t} = {Y_0} + \frac{{t - {t_0}}}{{a + b\left( {t - {t_o}} \right)}} $ | (7) |
通过上述公式改进和预测,发现预测精度有所提高,有效地减小了双曲线预测模型前期预测的偏差,使得预测曲线更加符合实际。
3 滨海抽水站沉降预测方法滨海抽水站是通榆河北延送水工程的第一级泵站,于2009年底建成,位于江苏省盐城市滨海县大套乡境内,东侧为通榆河上的大套船闸、通榆河大套二站和盐城市通榆河枢纽管理处。滨海抽水站自建成以来,累计沉降量呈逐年增加态势,每年期间沉降量在5 mm波动,其中2012-11、2014-09垂直位移发生了回弹上升2~5 mm,2014年9月至11月又急速沉降了5~8 mm左右,各部位沉降量直至2016年开始有所减小,累计沉降量仍呈增加态势,逐渐趋于稳定。本文针对该沉降情况进行了沉降预测方法模型研究。
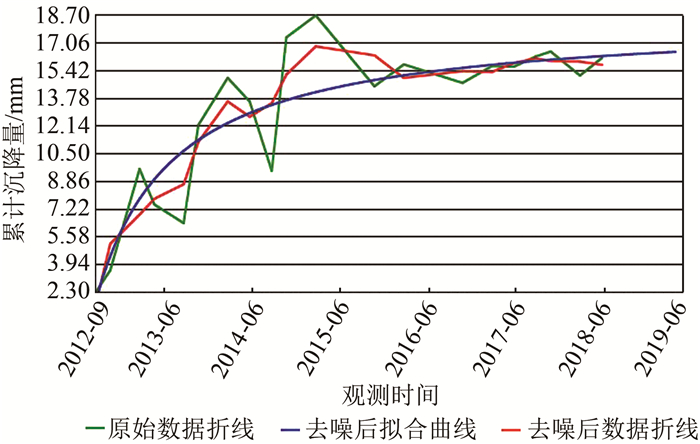
3.1 小波去噪前后的改进的双曲线沉降预测小波去噪的目是对测量所带来的粗差和噪声进行剔除,然后对测量数据进行重构,根据重构后的数据列解算预测公式中的参数[8]。本文通过Matlab编程实现小波去噪,首先将数据读取存入数组,对数组设置尺度向量和小波函数,本文选用db4函数,然后设置阈值向量,对高频系数进行阈值处理,最后对修正后的小波分解结构进行重构,得到新的数组,即为去噪后的数据[9]。将Matlab程序写成函数封装成dll程序集,C#进行集成调用,混合编程实现去噪前后的沉降预测曲线绘制。图 1为去噪前使用改进的双曲线预测模型绘制的沉降曲线;图 2为经过小波去噪后,对去噪后数据进行改进的双曲线预测结果。
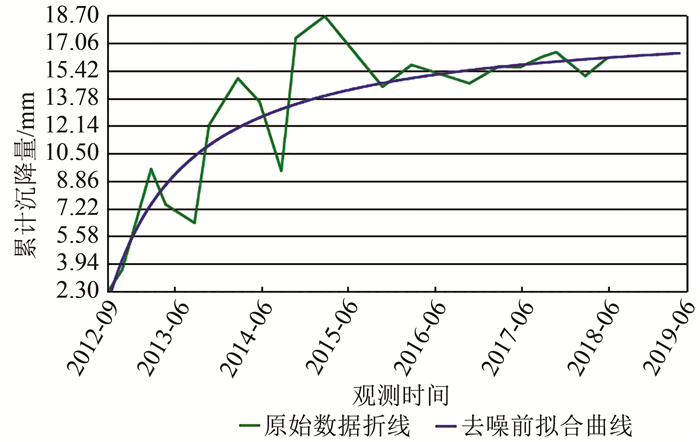 |
| 图 1 未去噪改进双曲线预测结果图 Fig.1 Prediction Result of Improved Hyperbola Without Denoising |
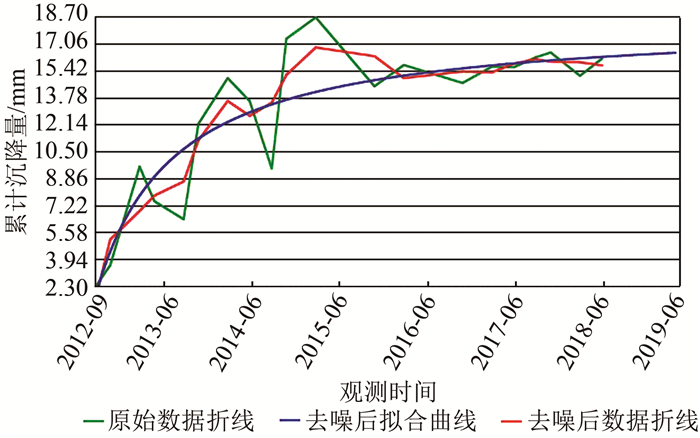 |
| 图 2 小波去噪后改进双曲线预测结果图 Fig.2 Prediction Result of Improved Hyperbola After Wavelet Denoising |
残差平方和是在线性模型中衡量模型拟合程度的一个量,用连续曲线近似地刻画或比拟平面上离散点组,以表示坐标之间函数关系的一种数据处理方法[10]。残差平方和(root-sum square, RSS)的计算公式如下:
| $ {\rm{RSS = }}{\sum\limits_{i = 1}^n {\left( {{y_i} - {{\hat y}_i}} \right)} ^2} $ | (8) |
式中,yi表示观测值;
相关系数R2(拟合优度)是指回归曲线对观测值的拟合程度,衡量的是回归方程整体的拟合度,是表达因变量与所有自变量之间的总体关系[11]。拟合优度的公式如下:
| $ {R^2} = 1 - \frac{{{\rm{RSS}}}}{{{\rm{TSS}}}} $ | (9) |
式中,RSS表示上述的残差平方和;TSS表示的是总体平方和。TSS计算公式如下:
| $ {\rm{TSS = }}{\sum\limits_{i = 1}^n {\left( {{y_i} - {{\bar y}_i}} \right)} ^2} $ | (10) |
本文通过残差平方和、拟合优度两个指标来对预测精度进行评价,残差平方和越小,拟合越好,预测精度越高;拟合优度越大,预测精度越高,最大值为1[12]。对图 1、图 2中的残差平方和、相关系数R2(拟合优度)进行整理,得到的精度对比如表 1所示。
| 表 1 改进的双曲线预测模型去噪前后预测精度对比 Tab.1 Comparison of Prediction Accuracy Before and After Denoising of Improved Hyperbolic Prediction Model |
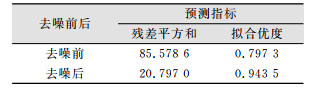 |
从图 1、图 2和表 1可以看出,经过小波去噪后再进行改进的双曲线沉降预测,精度有很大提高,残差平方和从85.578 6降到20.797 0,拟合优度从0.797 3提升到0.943 5,已经接近1,预测精度明显提高。
3.2 小波去噪后的不同沉降预测模型比较分析为了考察改进的双曲线沉降预测精度,考虑到经过小波去噪后预测精度大大提高,所以本文对小波去噪后的多项式趋势预测模型、对数函数趋势模型、幂函数趋势模型、指数函数趋势模型、双曲线预测模型和改进的双曲线预测模型等进行沉降预测,比较不同预测模型的预测精度。使用C#进行编程,计算绘制出不同预测模型预测结果图,如图 3所示。
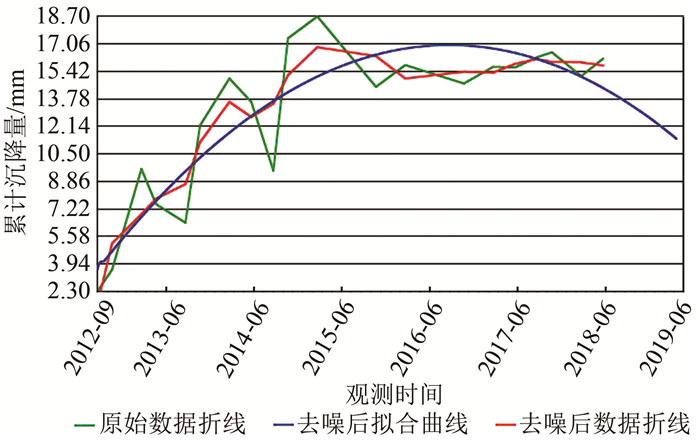 |
| 图 3 多项式拟合预测模型预测结果图 Fig.3 Prediction Results of Polynomial Fitting Prediction Model |
从图 3~图 8可以看出,经过改进的双曲线预测模型预测曲线与实际观测比较符合,预测效果良好,对数函数和双曲线预测模型基本达到预期效果,对计算出的精度指标残差平方和、拟合优度进行统计,结果如表 2所示。
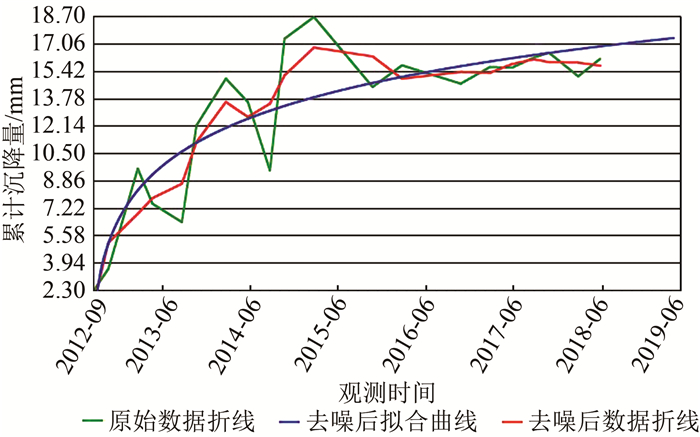 |
| 图 4 对数函数预测模型预测结果图 Fig.4 Prediction Results of Log Function Prediction Model |
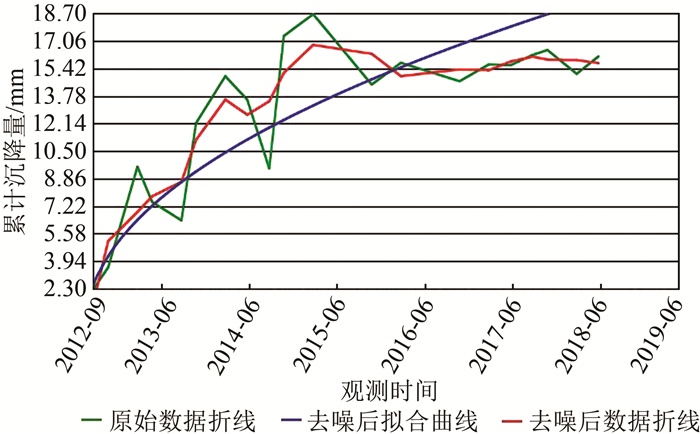 |
| 图 5 幂函数预测模型预测结果图 Fig.5 Prediction Results of Power Function Prediction Model |
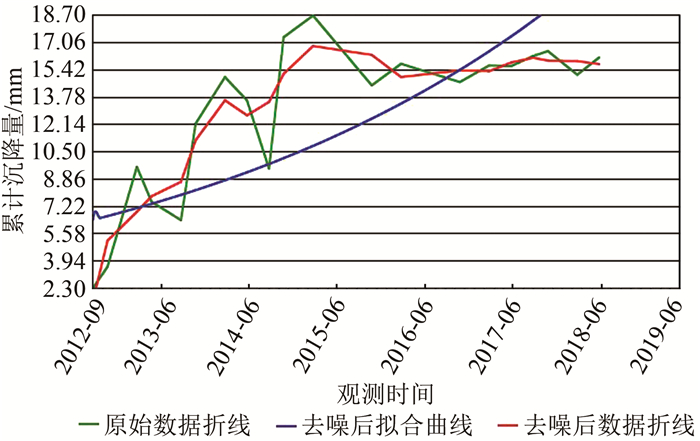 |
| 图 6 指数函数预测模型预测结果图 Fig.6 Prediction Results of Exponential Function Prediction Model |
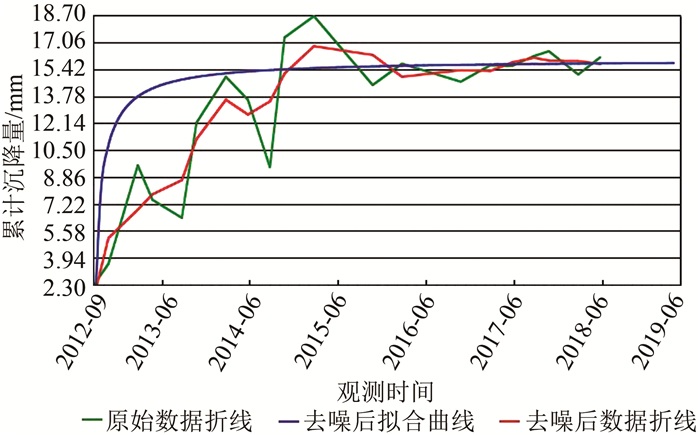 |
| 图 7 双曲线预测模型预测结果图 Fig.7 Prediction Results of Hyperbolic Prediction Model |
 |
| 图 8 改进的双曲线预测模型预测结果图 Fig.8 Prediction Results of Improved Hyperbolic Prediction Model |
| 表 2 去噪后不同沉降预测模型精度比较 Tab.2 Precision Comparison of Different Settlement Prediction Models After Noise Removal |
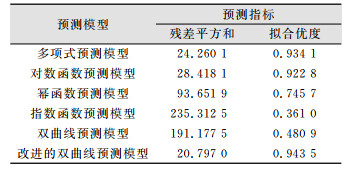 |
表 2的结果显示,改进的双曲线预测模型预测精度最高,其次是多项式和对数预测模型,但结合图 3~图 8可知,多项式预测模型前期预测较好,后期预测效果较差,原因可能是阶数取值有误,双曲线预测模型前期较差,后期预测较好,经过改进后的双曲线预测模型前后期预测效果最佳,残差平方和最低为20.797 0,相关系数R2(拟合优度)0.943 5也接近1。综上所述,小波去噪后的改进双曲线预测模型预测精度较其他模型有所改善[13]。
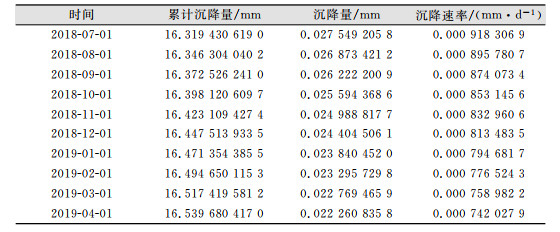
工程应用中,往往需要对预测值进行报表统计,计算出沉降量、累计沉降量和沉降速率等信息,方便进行差异沉降的计算,为是否有裂缝的产生做预测准备[14]。滨海抽水站主要分为上左翼、下左翼、上右翼、下右翼和底板5个部位,该5个部位布置了大量监测点。其中,本文对底板部位的其中一个监测点1~4应用小波去噪后的改进双曲线预测模型预测,结果报表如表 3所示。
| 表 3 小波去噪后的改进双曲线预测模型预测报表 Tab.3 Prediction Report of Improved Hyperbolic Prediction Model After Wavelet Denoising |
 |
4 结束语
工程中沉降预测问题直接关系到安全隐患,对沉降预测方法进行研究,能够对安全隐患作出准确预报,从而降低施工风险[15-23]。本文在小波去噪理论和回归分析理论的基础上来分析研究不同沉降预测模型的预测精度,并对经典理论公式进行改进,提高预测效果。从表 1研究结果发现,经过小波去噪后的沉降预测精度较未经过小波去噪进行沉降预测有很大提高,同时,从图 3及表 2研究结果发现,对数函数趋势模型和多项式趋势模型虽然残差平方和较小,拟合优度较高,但图 3和图 4显示前期预测精度高,后期效果不佳,曲线发生了急速下滑和上升,函数不收敛;从表 2可以看出,幂函数和指数函数预测模型的预测效果较其他几种模型差;双曲线预测模型前期效果不佳,后期达到预期效果,残差平方和较大,拟合优度也不好。针对这些不足,本文提出的改进型双曲线预测模型有效地保证了前期预测效果,同时又提高了后期的预测精度,而且相较于其他模型,该模型的预测残差平方小,拟合优度大,总体效果有所改善。
| [1] |
郭健, 查吕应, 庞有超, 等. 基于小波分析的深基坑地表沉降预测研究[J]. 岩土工程学报, 2014, 36(S2): 343-347. |
| [2] |
吴锋波, 金淮, 尚彦军, 等. 城市轨道交通隧道周边建(构)筑沉降预测方法研究[J]. 岩土力学与工程学报, 2013, 32(S2): 3535-3544. |
| [3] |
明祖涛, 刘军, 夏力, 等. 改进的灰色模型在高铁沉降预测中的应用[J]. 测绘科学, 2015, 40(4): 137-140. |
| [4] |
薛君. 高速公路路基沉降预测研究分析[J]. 北方交通, 2018(8): 53-55. |
| [5] |
龚循强, 熊小容, 周秀芳. 高铁桥墩沉降预测方法研究[J]. 测绘通报, 2014(4): 48-50. |
| [6] |
史汉新. 基于ArcGIS的矢量地形图符号化的设计与实现[J]. 现代测绘, 2010, 33(1): 59-61. |
| [7] |
余芳涛, 王永鑫, 张玉. 黄土地层地铁暗挖隧道地表纵向沉降规律及其预测分析方法[J]. 岩土力学, 2015, 36(S1): 287-292. |
| [8] |
张涛, 蔡国军, 刘松玉. 基于Weibull模型的软土路基沉降预测方法[J]. 岩土工程学报, 2013, 35(S2): 212-216. |
| [9] |
吴清海. 基于非等间距模型的建筑物沉降预测方法研究[J]. 测绘科学, 2008, 33(3): 59-61. |
| [10] |
刘小强. 基于自回归模型的基坑周边建筑物沉降预测分析[J]. 河南科技, 2015(18): 86-87. |
| [11] |
洪雪倩, 陈冠宇, 周超, 等. 基于小波去噪的灰色Verhulst模型在高铁路基沉降预测的应用[J]. 测绘与空间地理信息, 2018, 41(8): 123-126. |
| [12] |
梁永平, 严丽萍. 基于小波消噪的动态灰色桥墩沉降预测模型[J]. 测绘地理信息, 2017, 42(6): 65-68. |
| [13] |
胡伟明.基于小波和时间序列分析的高速铁路沉降预测方法研究[D].成都: 西南交通大学, 2011 http://d.wanfangdata.com.cn/Thesis/Y2107315
|
| [14] |
蔡东健, 岳建平, 成微, 等. 基于遗传算法的小波神经网络模型及其在地面沉降监控中的应用[J]. 测绘通报, 2010(8): 34-36. |
| [15] |
魏健.小波人工神经网络在建筑沉降预测中的应用研究[D].北京: 北京交通大学, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10004-1013279180.htm
|
| [16] |
张守魁. 高层建筑沉降监测与预测分析[J]. 西部资源, 2017(1): 62-63. |
| [17] |
陈银甲. 小波支持向量机在建筑沉降预测中的研究[J]. 山西建筑, 2017, 43(8): 201-202. |
| [18] |
杨根新, 杨建文. 灰色Verhulst模型在高层建筑沉降预测中的应用[J]. 勘察科学技术, 2014(6): 43-44. |
| [19] |
王亮, 罗新宇. BP神经网络模型在建筑沉降预测中的应用[J]. 福建建材, 2013(7): 20-21. |
| [20] |
魏健, 胡吉平, 谭衢霖, 等. BP神经网络在高层建筑沉降预测中的应用[J]. 北京测绘, 2013(2): 25-27. |
| [21] |
王保民, 巩耀娜. 建筑沉降预测方法的研究[J]. 工程质量, 2012, 30(3): 53-55. |
| [22] |
陈青.在高层建筑沉降预测中组合模型的应用研究[D].昆明: 昆明理工大学, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10674-1012264813.htm
|
| [23] |
王双龙. 基于灰色Verhulst模型的建筑工后沉降预测[J]. 测绘通报, 2007(10): 10-12. |
 2020, Vol. 45
2020, Vol. 45

