| 一种等高线数据格式与STL文件格式转换方法 |
地形图是表示地形起伏和高程分布,其所展示的信息内容是空间信息库建立的重要内容。目前,地理信息数据多是通过软件模拟观察进而解决实际问题,但物理模型较数字模型更有优势,对于复杂的地形而言,三维实体比等高线数据更便于人们理解。因此,地形图的实体建模和制造已经成为一个发展趋势和方向。3D打印技术的出现,给地理信息数据的实物制造提供了途径和方法。通过3D打印技术,可以方便快捷实现地形图的实体建模,从而充分发挥地理信息数据的模拟功能、信息载负功能、信息传输功能和认识功能。
目前,增材制造标准接口文件STL(stereo lithography)跨平台性良好被广泛研究和应用。对于增材制造工作者,所获取的地形图相关信息模型大多为等高线数据。因此,使用增材制造装备来制作地形图模型,就要突破等高线数据与STL数据转换的技术壁垒[1, 2]。
国内外学者已经尝试过利用增材制造技术来制作地形物理模型,但其中大部分是通过商业软件,经过多个软件包的多个步骤才能将GIS中的数据转换成STL文件[3, 4]。Bailey[5]在2005年使用数据制作加拿大火灾模型,但没指定数据格式及数据格式转换方法的规范化方面的叙述。Agrawal等[6]在2006年通过算法将数字高程模型(digital elevation model, DEM)数据转换为STL表面数据,将其导入Magics RP软件中从而获得最终可用于3D打印机的STL实体数据,但处理过程繁琐,难度较大。将DEM数据转换为STL格式的自主开发算法,省去了对地形数据的简化与修复,生成的STL文件可能出现裂纹、孤立面、顶点错误、法矢量错误、重叠面等缺陷,影响到后续打印的数据处理,以及打印模型的最终质量。
作为增材制造通用的打印格式,STL文件格式是一种用三角面片来表达实体表面数据的文件格式,文件结构主要有ASCII和二进制两种格式[7]。它是若干空间小三角形面片的集合,每个三角形面片用三角形的3个顶点和指向模型外部的法向量表示[8]。将所有等高线上提取的特征点视为点云集合,对其进行三角剖分运算,即可形成STL格式三角网格。
本文针对大幅面复杂地形图,利用已有的成熟技术手段得到的描述地形图常用的等高线数据,通过等距离散算法及Delaunay三角剖分算法,将等高线数据直接转换为可用于增材制造设备的STL三维模型,减少了数据处理过程中冗杂的处理步骤,能快速、高效地实现大幅面复杂等高线数据格式与STL格式的转换,并且在过程中,可以通过参数的调配对地形数据进行简化与修复。
1 等高线数据的离散化技术路线如图 1所示。
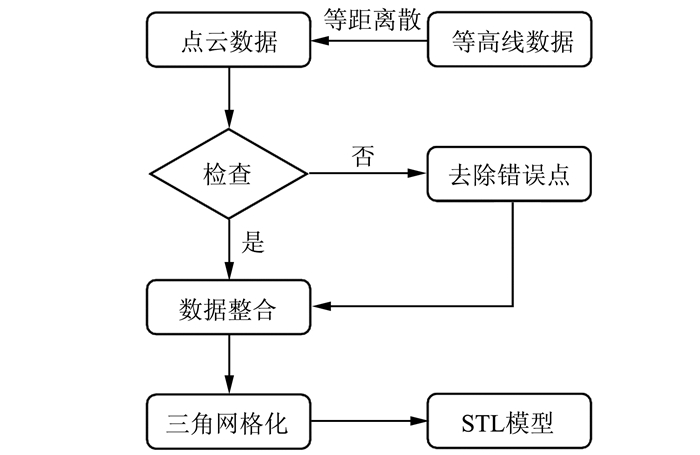 |
| 图 1 技术路线图 Fig.1 Flow Chart of Technology Road Map |
对于增材制造技术人员,所获取的地形图数据一般为等高线数据。因为等高线需要线宽和标高等属性,而样条曲线缺少一些属性,所以等高线线性数据中线条的本质一般为多段线,不用样条曲线,否则还需要对其进行转换,多段线越密集平顺,拟合后所形成的曲线效果越好。因此,获取等高线节点可以采用一种便捷有效的获取方法——等距离散。在等高线上定义一点A0,设A0的坐标为P0(x0,y0),沿等高线每隔距离Δd取下一点A1,以此类推,设定合适可控的Δd值,即可在曲线上获取若干特征点,以用于表征此曲线的特征。
按照以上计算方法,设置可控的Δa值,即可将等高线进行等距离散,在其上形成若干个离散点,随着Δa值的变化,所生成的地形图模型的复杂程度和表面精度也随之变化,根据需要对Δa值进行调整可提高打印效率。
2 特征点的三角剖分给定一平面上u个点的集合U={Ui|=1, …,u}。使用彼此不相交的直线段连接每个Um与Un,1≤m,n≤s,m≠n,构造出的图形满足:不存在相交的边;不包含集合U中除端点以外的任何其他点;所有面均为三角形,所有面的集合即U的集合的边界。在此基础上,假设上述形成的剖分集合中的端点(a,b)的一条边为γ,该集合中的其他点均不在经过点(a,b)的圆内,最多3点共圆。集合U的三角剖分中的所有边均具有γ边的特性,则此三角剖分为Delaunay三角剖分[9]。
Delaunay三角网[9]具有两个独有的特性:①Delaunay三角网是唯一的,其外接圆不含有面内的其他点; ②在散点集可能形成的三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大,这两个特性保证了Delaunay三角网中不会出现过于狭长的三角形,使得三角网的构建更合理准确,具有极大的应用价值。Delaunay三角网的数据结构简单,处理方便,存储效率高,与不规则的地形图特征和谐一致,易于更新[9]。
采用Delaunay三角剖分径向扫描算法[9, 10]:①寻找距离质心最近的点并将其作为起始点,将点集内除中心点外的其他所有点按照与中心点的距离和方向角从小到大升序排列;②进行径向扫描,连接中心点和其他所有点形成扇形,通过连接扇形的两个点形成扇形三角网,其中,方向角相同的点,通过其公共边的两侧分别生成一个三角形;③连接边界上的径向三角形的定点,在第一次扫描外边过程中用一组数组记录外包边上的相连边,下一次扫描时就能直接定位到下条边,填充扇形的凹域,向外生成新的三角形,直到和点集的外部边界重合;④由边界上的三角形向内检查由两个相邻三角形组成凸四边形的对角线,形成优化三角网。
通过上述算法,以某地区地形图为例,将地形图等高线数据,转化成STL三角网格面数据,如图 2所示。图 2(a)为所获取的某地区大幅面地形图等高线数据; 图 2(b)为经过三角剖分后形成的地形图STL面片; 图 2(c)为图 2(b)中箭头点A标记处的局部放大图,可以看出三角剖分所组成的面片形状。
 |
| 图 2 地形图等高线数据转化为STL三角网格面数据示意图 Fig.2 Result of Transforming Contour Data Formats to STL Data Formats |
将原始数据与得到的STL模型进行精度对比评价,如图 3所示。从图 3看出,STL曲面片与原始数据的偏差分布,平均误差为-0.600 0~+0.600 0 mm,其中,96.44%的数据偏差在±0.300 0 m范围内,曲面精度较高。
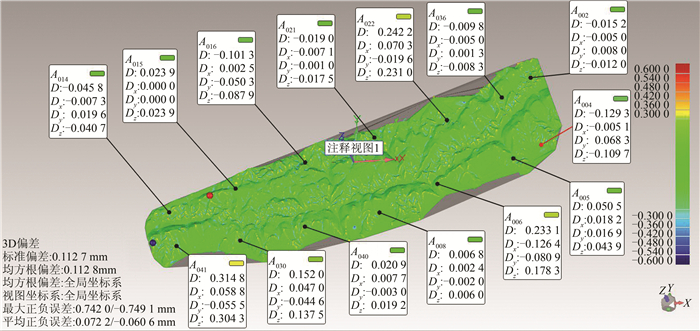 |
| 图 3 STL模型精度评价 Fig.3 STL Model Accuracy Evaluation |
将得到的STL模型输入Geomagic进行优化处理,可将其转换为STL实体模型,供后续打印使用。
3 结束语本文针对大幅面复杂等高线地形图的3D打印,提出了基于等高线地形数据与增材制造STL文件的对接方法,将等高线等距离散形成点云数据,再使用Delaunay三角剖分径向扫描算法,将其转换为可应用3D打印的STL模型。解决了地形图 3D打印三维模型获取的难题,为地形图的3D打印提供了便利条件。
| [1] |
应申, 郭仁忠, 李霖. 应用3D GIS实现三维地籍:实践与挑战[J]. 测绘地理信息, 2018, 43(2): 1-6. |
| [2] |
李精忠, 陈凯. 大数据时代数字地图制图课程教学改革的思考[J]. 测绘地理信息, 2017, 42(3): 121-123. |
| [3] |
Wu Tong, Cheung E H M. Enhanced STL[J]. International Journal of Advanced Manufacturing Technology, 2006, 29(11): 1 143-1 150. |
| [4] |
胡金星, 吴焕萍, 潘懋, 等. 基于格网划分的海量DEM数据生成[J]. 计算机辅助设计与图形学学报, 2004, 16(1): 41-44. DOI:10.3321/j.issn:1003-9775.2004.01.007 |
| [5] |
Bailey M. Layered Manufacturing for Scientific Visua-lization[J]. Communications of the ACM, 2005, 48(6): 42-48. DOI:10.1145/1064830.1064857 |
| [6] |
Agrawal S, Antunes J P, Theron E, et al. Physical Modelling of Catchment Area by Rapid Prototyping Using GIS Data[J]. Rapid Prototyping Journal, 2006, 12(2): 78-85. DOI:10.1108/13552540610652410 |
| [7] |
何强.基于虚拟现实技术的机械工程专业数字教学系统开发研究[D].济南: 山东建筑大学, 2013
|
| [8] |
朱虎, 杨忠凤, 张伟. STL文件的应用与研究进展[J]. 机床与液压, 2009, 37(6): 186-189. DOI:10.3969/j.issn.1001-3881.2009.06.063 |
| [9] |
李凤霞, 刘咏梅, 王晓哲, 等. 一种基于映射法的散乱点云Delaunay三角剖分算法[J]. 计算机应用研究, 2015, 32(3): 950-953. DOI:10.3969/j.issn.1001-3695.2015.03.072 |
| [10] |
邵春丽, 胡鹏, 黄承义, 等. DELAUNAY三角网的算法详述及其应用发展前景[J]. 测绘科学, 2004, 28(6): 68-71. DOI:10.3771/j.issn.1009-2307.2004.06.016 |
 2019, Vol. 44
2019, Vol. 44

