| 面向工作者的空间众包动态任务规划算法 |
2. 深圳大学建筑与城市规划学院城市空间信息工程系,广东 深圳, 518060;
3. 深圳大学空间信息智能感知与服务深圳市重点实验室,广东 深圳, 518060;
4. 深圳大学深圳大学智慧城市研究院,广东 深圳, 518060
2. Department of Urban Informatics, School of Architecture and Urban Planning, Shenzhen University, Shenzhen 518060, China;
3. Shenzhen Key Laboratory of Spatial Smart Sensing and Services, Shenzhen University, Shenzhen 518060, China;
4. Research Institute for Smart Cities, Shenzhen University, Shenzhen 518060, China
众包是通过互联网把一些任务外包给非特定的人群,使任务得到轻松解决的做法[1-4]。基于众包思想和时空大数据,产生了许多新应用,如道路交通监控、地图数据更新等。同时,也开始出现空间众包商业平台,如Uber、滴滴出行、人人快递等。
空间众包任务规划可分为两类。第一类面向众包平台,顾及众包工作者之间的竞争关系对工作者和任务进行匹配,以求众包平台利益最大化。Deng等[5]从平台分配的角度,对空间众包任务规划问题做了大量研究。第二类研究面向众包工作者,使众包工作者执行的任务量最大化。Deng等[6]最先把单个人的空间众包任务规划问题归纳为最大任务量规划问题(maximum task scheduling,MTS),在此基础上,Li等[7]提出动态环境下的在线任务规划,得出一种启发式算法加速求解。
本文基于单个众包工作者的动态任务规划在动态环境下进行求解,空间众包平台上任务不是全部已知,而是随时间依次出现,这样的模型更符合实际应用场景[8, 9]。本文主要提出了带有开始位置和结束位置的空间众包任务模型,适用于交通物流领域;同时提出了动态优化框架,用时空邻近算法产生初始解,并用禁忌搜索方法提高每个动态阶段的最优解。
1 问题定义针对带有起止点的空间众包任务模型和最大任务量动态路径规划问题给出问题定义。
定义1 空间众包任务。在交通物流场景下,空间众包任务(统称任务)用s{lo, ld, tr, td}表示。lo、ld、tr、td分别表示任务的开始地点、结束地点、开始时间和截止时间。一个众包工作者要截止时间td之前到达任务的结束地ld完成该任务。
定义2 空间众包工作者。空间众包工作者(统称工作者)指执行任务的人,用w{lw, rw, dw}表示。lw、rw、dw分别表示工作者当前位置、工作者的任务半径和工作截止时间。工作者位于lw时能接受lw为中心半径为rw内的任务,且该工作者能接受的任务开始时间不能超过dw。
定义3 最大任务量动态任务规划。给定一个任务集T{S1, S2, …, Sn},Si为一动态区间内的任务集,Ni为在Si内规划的最大任务量。最大任务量动态任务规划是在T中向工作者规划任务的过程,使
任务被执行应该满足以下约束:①距离约束:被执行任务si的起点必须在工作者的搜索半径内;②时间约束:工作者必须在任务截止时间之前到达任务结束点;③不变性约束:已经规划好的任务,不能改变。
如图 1所示,si表示任务i的起始地点,si′ 表示任务i的结束地点,工作者单位时间移动一个网格。假设工作者初始位置为(0, 5),搜索半径为3网格,每个任务有一个开始时间和截止时间。tnow=0时,任务s1发布该任务截止时间是8,该任务起始点在工作者的搜索范围内,工作者访问s1的起点(1, 4),之后访问终点s1′ (2, 3)并完成任务s1,此时tnow=4,任务s2已发布,工作者依次访问s2起点(5, 3)终点s2′ (3, 2)。以此类推,该工作者规划的MTS路径是:s1→s2→s3。
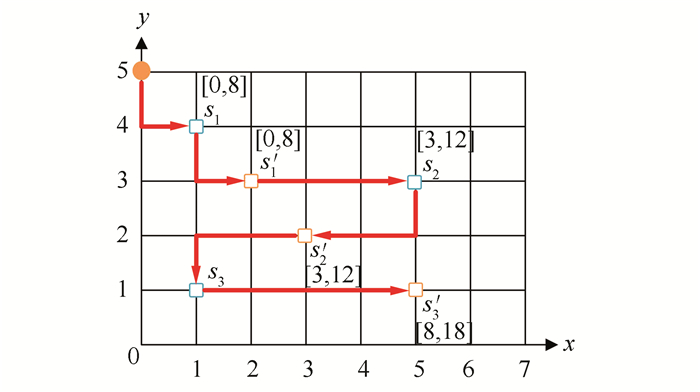 |
| 图 1 单个众包工作者路径规划示意图 Fig.1 Task Scheduling for a Worker |
2 算法设计 2.1 动态优化框架
本文提出基于时间阈值α触发的动态优化框架,动态任务收集模块不断收集进入系统的任务,当收集时长等于α时触发任务规划机制算法:生成一个初始解,经过迭代优化后发布规划结果,完成一个动态区间的优化。若有新的任务出现,系统继续收集新任务进入下一个动态区间,反之结束算法。
2.2 初始解生成算法本文用时空邻近算法(nearest spatial-temporal heuristic, NSH)生成初始解,工作者执行时空距离最近任务。时空邻近算法综合考虑工作者与任务之间空间邻近性和任务完成时间的急迫性,能生成较高质量的初始解, 时空距离st为:
| $ {s_t} = \rho \times d + \sigma \times t $ | (1) |
式中,d表示空间距离;t表示任务截止时间与工作者当前时间tnow的时间差;ρ和σ为距离与时间的权重,默认设置为1。
3 禁忌搜索算法为了进一步提高解的质量,本文利用禁忌搜索算法(tabu search, TS)对初始解进行优化。禁忌搜索在组合优化中被广泛应用[10]。禁忌搜索算法的基本思想是通过建立禁忌表来避免陷入局部最优。
1) 评价函数是对当前解优劣的评价指标。评价函数e(r)为:
| $ e\left( r \right) = p + d(r) $ | (2) |
式中,r为已规划的路径;d(r)为工作者旅行成本;p为不满足约束的惩罚值。
2) 本文设计了内部互换、内外互换、插入3种邻域变换规则。内部互换:在已经规划的任务序列中随机选取两个任务交换执行顺序;内外互换:在已规划与未规划的任务中随机各选一个任务点进行互换;插入:在未规划的任务中随机选择一个任务插入邻近的已规划任务序列中。3种邻域变换规则使用概率相等。
3) 禁忌表是保存禁忌对象的一种先进先出的数据结构,本文禁忌对象为在邻域变换中进行互换或插入的任务点。禁忌长度是影响禁忌搜索算法质量的一个很重要的因素。如果禁忌长度太短,可能会陷入局部最优;如果过长,会增加计算时间。本文使用固定的禁忌长度
实验环境:处理器为2.5 GHz Inter(R) Core(TM) i7-4710MQ, 内存为8 GB,操作系统为Windows 10,编程语言为python。
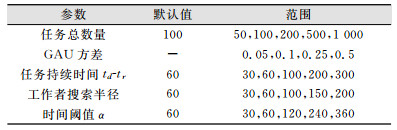
数据集设置如下:任务空间分布在100×100的网格内,并服从均匀分布(uniform distrition, UNI)或高斯分布(gaussian distribution, GAU),工作者单位时间移动一个网格。数据集的具体参数设置如表 1所示,当讨论一个参数变化时,其他参数使用默认值。
| 表 1 数据集参数表 Tab.1 Statistics of Experimental Data |
 |
类似文献[8],本文用竞争比(competitive ratio, CR)和任务响应时间来衡量动态路径规划算法的性能。任务响应时间是指计算所耗费的总时间除以任务总数得出的平均时间。竞争比CR为:
| $ {\rm{CR}} = \frac{{{R_{{\rm{alg}}}}\left( T \right)}}{{{R_{{\rm{opt}}}}(T)}} $ | (3) |
式中,Ralg(T)表示用某个算法得到的规划任务数量;Ropt(T)表示在静态环境下得到的最优规划任务数量。
为了验证时空邻近算法的性能将本文方法与文献[8]中提出的3种算法进行比较。①随机算法(random heuristic, RH):该算法在动态任务集中随机选取一个满足约束的任务序列作为初始解; ②时间邻近算法(earliest deadline heuristic, EDH):该算法的基本思路是先到先服务,优先执行发布时间靠前的任务; ③空间邻近算法(nearest neighbor heuristic, NNH):该算法的原则是距离优先,优化执行距离工作者最近的任务。
4.2 实验结果与分析空间众包任务动态规划算法性能受任务数量、任务持续时间、空间分布、任务搜索半径、动态时间阈值的影响。利用上述实验数据集测试5个因素的算法敏感性。
1) 任务数量。图 2给出了不同任务数量下算法的表现,竞争比为0.71~0.80;禁忌搜索算法为0.82~0.93,在时空邻近算法的基础上提升了10%左右;空间邻近算法为0.55~0.68;时间邻近算法和随机算法表现相近,竞争比为0.33~0.49。随着任务数量的增加,每个任务的响应时间有上升的趋势,具体每次响应时间为0.1~0.3 s,可以接受。
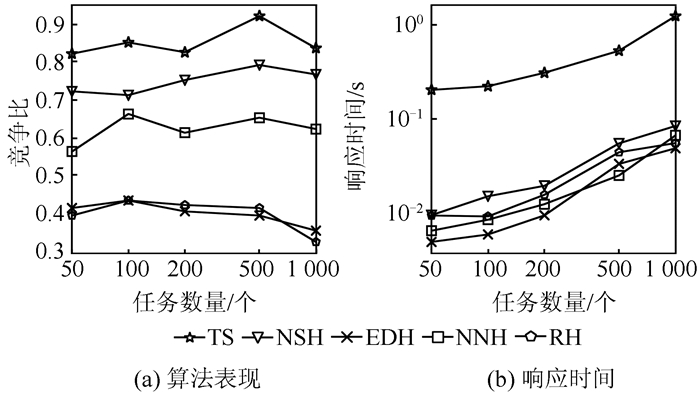 |
| 图 2 不同任务数量的算法表现 Fig.2 Performance on Different Number of Tasks |
2) 任务持续时间。如图 3所示,空间邻近算法的竞争比随着任务持续时间的增大而增大,而其他算法几乎不受影响。由于任务持续时间增大,使某些动态区间内的任务增多,同时空间邻近任务也增多,故该算法能得到更多的任务。随着任务的持续时间的增加,获取每个任务的响应时间有所下降。
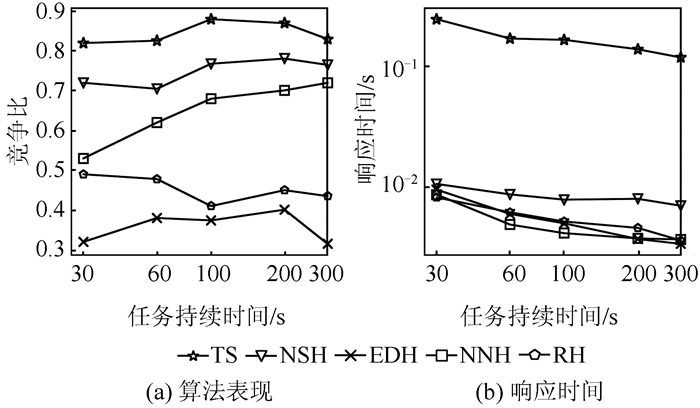 |
| 图 3 任务不同持续时间的算法表现 Fig.3 Performance on Different Task Durations |
3) 任务在空间上的分布具有一定的聚集特征,故该组实验设置了一组均匀分布和4组呈高斯分布,GAU方差分别为0.05、0.1、0.25、0.5。实验结果如图 4所示,从总体上看,随着任务空间分布的离散程度增大,禁忌搜索、时空邻近、时间邻近算法的完成任务数量逐渐减少。禁忌搜索算法在所有算法中表现最好,其次是时空邻近算法。空间邻近算法的表现随任务分布变化影响较小。
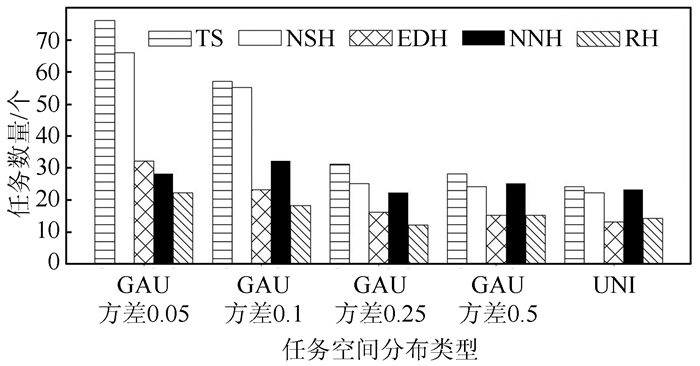 |
| 图 4 不同空间分布的算法表现 Fig.4 Performance on Different Spatial Distribution |
4) 图 5给出了工作者搜索半径变化不同算法的表现,随着搜索半径的增大随机算法竞争比减小,其他算法竞争比基本不变。对于随机算法,搜索半径较小即排除离工作者距离较远的任务,增加了其获取邻近任务的概率使结果更优。每个任务的响应时间,随着搜索半径的增大而增大。
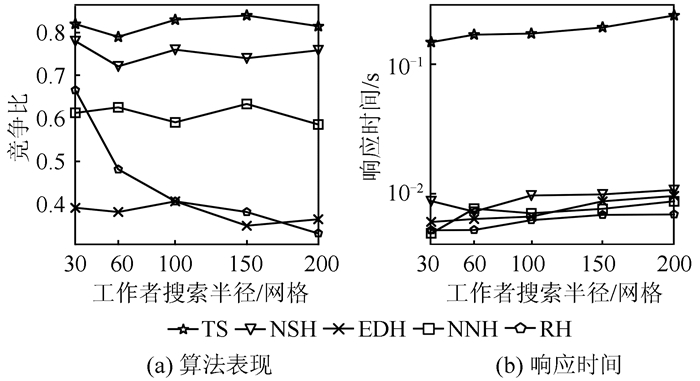 |
| 图 5 工作者不同搜索半径的算法表现 Fig.5 Performance on Different Search Radii of Worker |
5) 动态时间阈值越大,动态度越低越接近静态问题。不同动态时间阈值下算法表现如图 6所示,时空邻近算法与时间邻近算法几乎不受动态程度的影响。禁忌搜索算法随着动态时间阈值的增大竞争比有所增大,与之相反的,空间邻近算法和随机算法的竞争有所下降。时间邻近算法与时空邻近算法都考虑了时间邻近因素,故时间阈值的变化不会对其产生较大影响。对于随机算法和空间邻近算法,较小的时间阈值对动态区间内的任务在时间维度上具有一定的限制作用,故α较小时竞争比较大。每个任务的响应时间,随着动态时间阈值的增大而减小。
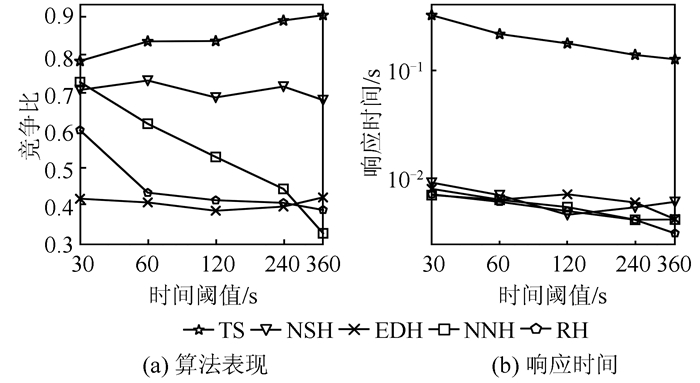 |
| 图 6 不同时间阈值的算法表现 Fig.6 Performance on Different α |
4.3 实验总结
通过实验发现,5种因素对不同的算法有着不同的影响。在初始解算法方面,时空邻近算法表现最好并且比较稳定,几乎不受数据和参数变化的影响。空间邻近算法对任务持续时间、任务分布以及动态时间阈值的变化都较为敏感。时间邻近算法表现较为稳定但解的质量较差。随机算法受工作者搜索半径和动态时间阈值的变化较为敏感,解质量较差。禁忌搜索算法基于时空邻近算法进行优化,算法稳定性强并且能在时空邻近算法解的基础上再优化10%左右。
5 结束语针对动态环境下的空间众包任务规划问题,本文对模型进行改进并设计了求解框架。模型方面:空间众包任务不仅仅是单个位置点,而是具有起始点和终点,这样的模型适用于交通物流领域的空间众包平台。求解方面:提出一种动态优化框架,基于该框架本文提出时空邻近算法生成初始解,并用禁忌搜索算法进一步提高解的质量。在实验中,时空邻近算法在不同的数据与参数下表现稳健,初始解的质量较高。禁忌搜索算法在时空邻近算法初始解的基础上进一步优化,解的质量提升10%左右。在后续工作中,需要考虑路径规划过程中多个工作者的竞争关系,站在平台全局最优的角度对多个工作者的路径规划。
| [1] |
Li G, Wang J, Zheng Y, et al. Crowdsourced Data Management: A Survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(9): 2296-2319. DOI:10.1109/TKDE.2016.2535242 |
| [2] |
Garciamolina H, Joglekar M, Marcus A, et al. Challenges in Data Crowdsourcing[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(4): 901-911. DOI:10.1109/TKDE.2016.2518669 |
| [3] |
童咏昕, 袁野, 成雨蓉, 等. 时空众包数据管理技术研究综述[J]. 软件学报, 2017, 28(1): 35-58. |
| [4] |
Tu W, Li Q, Fang Z, et al. A Novel Spatial-Temporal Voronoi Diagram-Based Heuristic Approach for Large-Scale Vehicle Routing Optimization with Time Constraints[J]. ISPRS International Journal of Geo-Information, 2015, 4(4): 2019-2044. DOI:10.3390/ijgi4042019 |
| [5] |
Deng D, Shahabi C, Demiryurek U. Maximizing the Number of Worker's Self-Selected Tasks in Spatial Crowdsourcing[C]. ACM Sigspatial International Conference on Advances in Geographic Information Systems, New York, 2013 https://www.researchgate.net/publication/262173870_Maximizing_the_number_of_worker's_self-selected_tasks_in_spatial_crowdsourcing
|
| [6] |
Deng D, Shahabi C, Zhu L. Task Matching and Scheduling for Multiple Workers in Spatial Crowdsourcing[C]. Sigspatial International Conference on Advances in Geographic Information Systems, New York, 2015 https://www.researchgate.net/publication/311489765_Task_matching_and_scheduling_for_multiple_workers_in_spatial_crowdsourcing
|
| [7] |
Li Y, Man L, Xu W. Oriented Online Route Recommendation for Spatial Crowdsourcing Task Workers[C]. International Symposium on Spatial and Temporal Databases, New York, 2015 https://rd.springer.com/chapter/10.1007/978-3-319-22363-6_8
|
| [8] |
To H, Shahabi C, Kazemi L. A Server-Assigned Spatial Crowdsourcing Framework[J]. ACM Transactions on Spatial Algorithms and Systems, 2015, 1(1): 1-28. |
| [9] |
Deng D, Shahabi C, Demiryurek U, et al. Task Selection in Spatial Crowdsourcing from Worker's Perspective[J]. Geoinformatica, 2016, 20(3): 529-568. DOI:10.1007/s10707-016-0251-4 |
| [10] |
Tu W, Li Q, Li Q, et al. A Spatial Parallel Heuristic Approach for Solving very Large-Scale Vehicle Routing Problems[J]. Transactions in GIS, 2017, 21(6): 1130-1147. DOI:10.1111/tgis.2017.21.issue-6 |
 2019, Vol. 44
2019, Vol. 44

